Στο άρθρο αυτό παρουσιάζουμε την προσομοίωση φαινομένων κοσμικής κλίμακας, όπως οι μαύρες τρύπες και η διαστολή του σύμπαντος, από μορφώματα ψυχρών ατόμων σε ένα εργαστήριο. Τα επιτεύγματα αυτά εδράζονται σε αναλογίες που υπάρχουν ανάμεσα στην επίδραση των βαρυτικών πεδίων στην τροχιά του φωτός και την κίνηση του φωτός μέσα σε οπτικά υλικά και ανοίγουν πρωτόγνωρους και απρόσμενους δρόμους στη μελέτη του σύμπαντος.
ΟΠΤΙΚΗ ΚΑΙ ΒΑΡΥΤΗΤΑ
Οι μαύρες τρύπες, αυτά τα εξωτικά ουράνια σώματα, έχουν εξάψει στην κυριολεξία τη φαντασία του κοινού. Αρκεί να θυμηθούμε τον θόρυβο που είχε προκληθεί πριν κάποια χρόνια με αφορμή κάποια από τα πειράματα που εξελίσσονταν στο CERN και την πιθανότητα να εμφανιστούν σε αυτά «μικροσκοπικές» μαύρες τρύπες έτοιμες να «καταβροχθίσουν» τα πάντα. Αυτό όμως που σίγουρα δεν έχει περάσει από το νου κανενός είναι η πιθανότητα αυτά τα αντικείμενα να παραχθούν σε ένα εργαστήριο σύγχρονης ατομικής φυσικής ή ακόμη περισσότερο, σε κάποια χρόνια, να πωλούνται και ως παιγνίδι. Ίσως αυτή η ημέρα να είναι πολύ κοντά, αλλά δεν υπάρχει κανένας λόγος πανικού. Αυτές οι «μαύρες» τρύπες θα είναι απόλυτα ασφαλείς και δεν πρόκειται να καταπιούν κανέναν!
Ας πάρουμε λίγο τα πράγματα από την αρχή. Στην Εικ.1 βλέπουμε ένα απλό πείραμα οπτικής: την κάμψη μιας δέσμης λέιζερ όταν αυτή περάσει από ένα δοχείο γεμάτο νερό στο οποίο έχουμε διαλύσει μερικούς κύβους ζάχαρης. Η αιτία της κάμψης είναι η διάθλαση της δέσμης από τα στρώματα με διαφορετικό δείκτη διάθλασης που σχηματίζονται στο διάλυμα. Αυτό συμβαίνει επειδή η συγκέντρωση της διαλυμένης ουσίας ελαττώνεται με την απόσταση από τον πυθμένα του δοχείου με αποτέλεσμα να δημιουργείται μια σχετικά ομαλή μεταβολή του δείκτη διάθλασης που κάμπτει την ακτίνα κατά συνεχή και εντυπωσιακό τρόπο. Με λίγη επιδεξιότητα από την πλευρά του πειραματιστή, η ακτίνα μπορεί να ανακλαστεί στον πυθμένα και έπειτα, ακολουθώντας πάλι καμπύλη τροχιά, να εξέλθει από το δοχείο.
Ας πάμε τώρα σε ένα εντελώς διαφορετικό φυσικό σύστημα. Στην Εικ.2 βλέπουμε την καμπύλωση της τροχιάς του φωτός, που καταφτάνει από ένα μακρυνό άστρο, όταν στην πορεία του βρεθεί ένα ουράνιο σώμα με μεγάλη μάζα, όπως ο Ήλιος, σύμφωνα με τις προβλέψεις της Γενικής Θεωρίας της Σχετικότητας (ΓΘΣ). Αυτό το φαινόμενο προκαλεί (όπως και η διάθλαση στην ατμόσφαιρα) την διαφορά ανάμεσα στην πραγματική και την φαινόμενη θέση ενός άστρου στον ουράνιο θόλο. Η αντιστοιχία ανάμεσα στις δύο εικόνες είναι προφανής και εκπληκτική: η πορεία του φωτός μέσα από ένα οπτικό υλικό “ισοδυναμεί” με την επίδραση μιας μεγάλης μάζας στην πορεία του όταν αυτό ταξιδεύει μέσα στο διάστημα. Η πρώτη περίπτωση είναι ένα καθαρά οπτικό φαινόμενο, ενώ η δεύτερη είναι αποτέλεσμα της βαρύτητας.
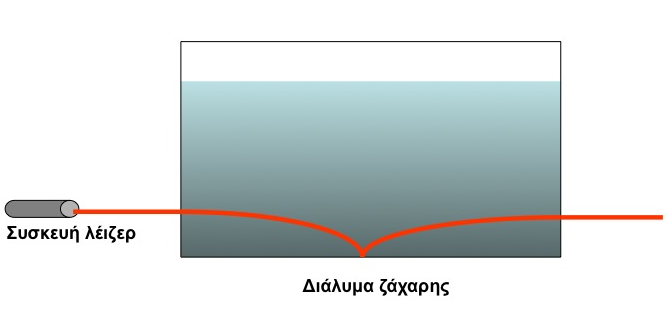
Εικόνα 1: Σε ένα δοχείο που περιέχει νερό έχουμε διαλύσει ζάχαρη. Εάν δεν ανακατέψουμε το διάλυμα, η συγκέντρωση της ζάχαρης είναι μεγάλη κοντά στον πυθμένα του δοχείου και ελαττώνεται βαθμιαία όσο πάμε προς τα πάνω. Αυτό έχει ως αποτέλεσμα τη δημιουργία στρωμάτων με διαφορετικό δείκτη διάθλασης που καμπυλώνουν την τροχιά της δέσμης λέιζερ.
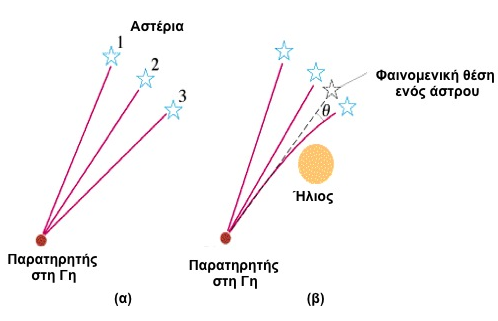
Εικόνα 2: Στο (α) δεν παρεμβάλλεται κάποιο μεγάλο ουράνιο σώμα μεταξύ των τριών άστρων και του παρατηρητή στη Γη. Στο (β) η παρουσία του Ήλιου προκαλεί την καμπύλωση των ακτινών από το φως ενός μακρινού άστρου (του τρίτου στη σειρά). Αυτό έχει ως αποτέλεσμα η φαινόμενη θέση του άστρου στον ουράνιο θόλο να είναι διαφορετική από την πραγματική.
Η βαρύτητα είναι η δύναμη που καθορίζει τις κινήσεις των πλανητών, των ηλιακών συστημάτων και των γαλαξιών, δηλαδή του Σύμπαντος. Οι κινήσεις αυτές είναι πολύ μεγάλης κλίμακας και η μελέτη τους βασίζεται σε δεδομένα που καταγράφονται από τηλεσκόπια, μετρήσεις πάνω στα φάσματα ακτινοβολιών που εκπέμπονται από τα ουράνια σώματα και εσχάτως από συστήματα ανίχνευσης βαρυτικών κυμάτων. Δυστυχώς, η απευθείας και επιτόπου μελέτη των ιδιοτήτων των ουρανίων σωμάτων περιορίζεται στους πλανήτες του ηλιακού μας συστήματος χάρις τα ταξίδια μη επανδρωμένων διαστημοπλοίων τα οποία διαρκούν πολλά χρόνια. Αφού λοιπόν δεν πάει ο Μωάμεθ στο βουνό ας έλθει το βουνό στον Μωάμεθ! Θα χρησιμοποιήσουμε την κάμψη που προκαλεί στο φως η διάθλαση, καθώς και άλλα οπτικά φαινόμενα, για να προσομοιώσουμε την επίδραση των ουρανίων σωμάτων στην τροχιά του φωτός. Τα τελευταία χρόνια η μελέτη τέτοιων προβλημάτων βρίσκεται σε άνθηση. Οι πολύπλοκες μαθηματικές σχέσεις της ΓΘΣ, για την μελέτη της επίδρασης των βαρυτικών πεδίων στην τροχιά του φωτός, έχουν κοινή μαθηματική δομή με τις εξισώσεις που περιγράφουν την κίνηση του φωτός μέσα σε οπτικά υλικά. Ένα τέτοιο πρόβλημα, που έχει γίνει προσπάθεια να μελετηθεί σε συστήματα παγιδευμένων ατόμων, είναι η επίδραση που έχει μια μαύρη τρύπα στην τροχιά του φωτός.
ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ ΚΑΙ ΟΠΤΙΚΗ
Με μια πρώτη ματιά η σχέση της ΓΘΣ με την Oπτική μπορεί να φανεί παράδοξη. Αυτό συμβαίνει επειδή έχουμε συνηθίσει να συνδέουμε αυτή τη σπουδαία φυσική θεωρία με προβλήματα βαρύτητας και κοσμολογίας. Η κατάσταση άλλαξε με την έλευση της Οπτικής Μετασχηματισμών (Transformation Optics) (Chen et al, 2010). Αυτό το πεδίο της φυσικής έχει αξιοποιήσει ιδέες που αναπτύχθηκαν στο πλαίσιο της ΓΘΣ για την κατασκευή αγώγιμων υλικών που είναι μη ανιχνεύσιμα από στατικά ηλεκτρικά πεδία (Greenleaf et al, 2003). Οι ιδέες αυτές άνοιξαν το δρόμο για την κατασκευή αόρατων διατάξεων (Leonhardt, 2006). Όμως η ιστορία αυτή έχει βαθύτερες ρίζες στο χρόνο.
To 1818 o A.-J. Fresnel διατύπωσε την ορθή άποψη, χρησιμοποιώντας ωστόσο τη θεωρία του αιθέρα, πως ένα κινούμενο μέσο θα παρασύρει μαζί του το φως όπως ο άνεμος τα φύλλα ενός δέντρου (Fresnel, 1818). Το φαινόμενο αυτό παρατηρήθηκε το 1851 από τον Η. Fizeau (Fizeau, 1851). Τέσσερις δεκαετίες αργότερα, το 1895, ο Η. Α. Lorentz μελέτησε ένα παρόμοιο φαινόμενο, που προέρχεται από την οπτική διασπορά[1] του φωτός (Lorentz, 1895). Οι προβλέψεις του Η. Α. Lorentz επαληθεύτηκαν, στη συνέχεια, πειραματικά από τον P. Zeeman (Zeeman, 1914). To 1923 o W. Gordon παρατήρησε ότι η κίνηση ισότροπων σωμάτων μέσα σε ηλεκτρομαγνητικά πεδία ισοδυναμεί με κίνηση μέσα σε συγκεκριμένες χωροχρονικές γεωμετρίες (Gordon, 1923). Ένα χρόνο αργότερα, το 1924, ο Ι. Υ. Tamm, αφού γενίκευσε αυτές τις θεωρίες, τις εφάρμοσε για να μελετήσει την διάδοση του φωτός σε μη επίπεδες γεωμετρίες (Tamm, 1924). Οι E. Bortolotti και S. M. Rytov απέδειξαν ότι αυτές οι γεωμετρίες έχουν μη Ευκλείδιο χαρακτήρα (Rytov, 1938). Το 1960 ο J. Plebanski θεμελείωσε τα ηλεκτρομαγνητικά φαινόμενα μέσα στον καμπύλο χωροχρόνο και το 1961 ο L. S. Dolin δημοσίευσε μια προδρομική εργασία πάνω στην οπτική μετασχηματισμών (Plebanski, 1960; Dolin, 1961). Το 1972 υπήρξε μια κομβική χρονιά καθώς ο W. Unruh, σε ένα σεμινάριο στην Οξφόρδη, επινόησε ένα απλό ανάλογο για τον ορίζοντα γεγονότων μιας μαύρης τρύπας. Σε αυτό το θέμα θα αναφερθούμε αναλυτικά στην επόμενη ενότητα. Τέλος, το 1999 αποδείχτηκε πως ένα κινούμενο διηλεκτρικό υλικό δρα στο φως όπως ένα βαρυτικό πεδίο και μάλιστα είναι δυνατόν να χρησιμοποιηθεί το εν λόγω φαινόμενο για να κατασκευαστούν προσομοιώσεις αστρονομικών φαινομένων σε ένα εργαστήριο φυσικής (Leonhardt, 1999). Αντίστοιχα φαινόμενα εμφανίζονται στη συμπεριφορά των ηχητικών κυμάτων σε κινούμενα ρευστά. Στην περίπτωση αυτή τα ηχητικά κύματα υπόκεινται σε μια χωροχρονική γεωμετρία που εξαρτάται από τη μορφή της ροής και την τοπική ταχύτητα του ήχου (White, 1973; Unruh, 1981).
| ‘Ετος | Επίτευγμα |
| 1818 | Ο A.-J. Fresnel διατύπωσε την ορθή άποψη, χρησιμοποιώντας ωστόσο τη θεωρία του αιθέρα, πως ένα κινούμενο μέσο θα παρασύρει μαζί του το φως όπως ο άνεμος τα φύλλα ενός δέντρου. |
| 1851 | Ο Η. Fizeau παρατηρεί το φαινόμενο που είχε προβλέψει ο Fresnel. |
| 1895 | Ο Η. Α. Lorentz προβλέπει θεωρητικά ένα παρόμοιο φαινόμενο που οφείλεται στη διασπορά του φωτός. |
| 1915 | Ο P. Zeeman επαληθεύει πειραματικά την πρόβλεψη του Lorentz. |
| 1923 | Ο W. Gordon παρατήρησε ότι η κίνηση ισότροπων σωμάτων μέσα σε ηλεκτρομαγνητικά πεδία ισοδυναμεί με κίνηση μέσα σε συγκεκριμένες χωροχρονικές γεωμετρίες. |
| 1924 | Ο Ι. Υ. Tamm, αφού γενίκευσε αυτές τις θεωρίες, τις εφάρμοσε για να μελετήσει την διάδοση του φωτός σε μη επίπεδες γεωμετρίες. |
| 1928 & 1936 | Οι E. Bortolotti και S. M. Rytov απέδειξαν ότι αυτές οι γεωμετρίες έχουν μη Ευκλείδιο χαρακτήρα |
| 1960 | Ο J. Plebanski θεμελίωσε τα ηλεκτρομαγνητικά φαινόμενα μέσα στον καμπύλο χωροχρόνο και το |
| 1961 | Ο L. S. Dolin δημοσίευσε μια προδρομική εργασία πάνω στην οπτική μετασχηματισμών |
| 1972 | Ο W. Unruh, σε ένα σεμινάριο στην Οξφόρδη, επινόησε ένα απλό ανάλογο για τον ορίζοντα γεγονότων μιας μαύρης τρύπας. |
| 1999 | Αποδείχτηκε από τον U. Leonhardt πως ένα κινούμενο διηλεκτρικό υλικό δρα στο φως ως ένα βαρυτικό πεδίο και μάλιστα είναι δυνατόν να χρησιμοποιηθεί το εν λόγω φαινόμενο για να κατασκευαστούν προσομοιώσεις αστρονομικών φαινομένων σε ένα εργαστήριο φυσικής |
ΟΙ ΟΠΤΙΚΕΣ ΜΑΥΡΕΣ ΤΡΥΠΕΣ
Μια μαύρη τρύπα χαρακτηρίζεται από έναν ορίζοντα γεγονότων. Πρόκειται για μια επιφάνεια όπου κάθε τι εντός της, ακόμη και το φως, δεν μπορεί να διαφύγει εξαιτίας του ισχυρού βαρυτικού πεδίου. Το 1981 ο W. Unruh υπέδειξε για πρώτη φορά μια πολύ απλή αναλογία για τον ορίζοντα γεγονότων μιας μαύρης τρύπας. Η πρότασή του άνοιξε στην κυριολεξία το δρόμο για όλες τις μετέπειτα πειραματικές προσπάθειες προσομοίωσης μιας μαύρης τρύπας.
Η ιδέα έχει ως εξής: φανταστείτε έναν άνθρωπο να κωπηλατεί μια μικρή βάρκα ενάντια στο ρεύμα ενός καταράκτη, που αναπαριστά μια μαύρη τρύπα (Eικ.3). Πέρα από ένα συγκεκριμένο σημείο, κοντά στον καταράκτη, το ρεύμα γίνεται τόσο ισχυρό ώστε ο κωπηλάτης δεν μπορεί να προσδώσει αρκετή ταχύτητα στη βάρκα και να δραπετεύσει από τον καταράκτη. Το σημείο αυτό αντιστοιχεί στον ορίζοντα γεγονότων. Στο ίδιο πνεύμα, στη συνέχεια, ο Unruh θεώρησε την περίπτωση όπου τα κύματα της θάλασσας κατευθύνονται προς το δέλτα ενός ποταμού (Εικ.4). Επειδή, όσο ανεβαίνουμε προς το ποτάμι, το ρεύμα γίνεται πολύ ισχυρό, τα κύματα μπορούν να φτάσουν μέχρι ενός σημείου. Υπό αυτήν την έννοια ο ποταμός είναι μια «λευκή» τρύπα, το αντίθετο μιας μαύρης τρύπας, όπου τίποτα δεν μπορεί να εισέλθει. Η λευκή τρύπα είναι μια υποθετική περιοχή του χωροχρόνου στην οποία δεν μπορεί να εισέλθει τίποτα ενώ μαζικά σωμάτια και φως μπορούν να διαφύγουν.

Εικόνα 3: Πέρα από ένα συγκεκριμένο σημείο, κοντά στον καταράκτη, το ρεύμα γίνεται τόσο ισχυρό – όπως ένας ορίζοντας γεγονότων – ώστε ο κωπηλάτης δεν μπορεί να προσδώσει αρκετή ταχύτητα στη βάρκα και να δραπετεύσει από τον καταράκτη. Ο ποταμός συμπεριφέρεται ως μια μαύρη τρύπα.
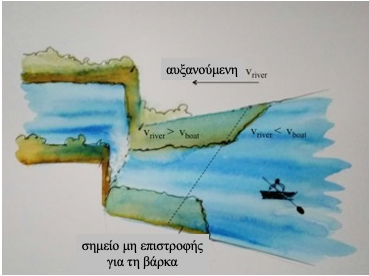
Εικόνα 4: Τα κύματα της θάλασσας κατευθύνονται προς το δέλτα ενός ποταμού και μαζί τους και η βάρκα. Επειδή το ρεύμα γίνεται πολύ ισχυρό όσο ανεβαίνουμε προς το ποτάμι, τα κύματα και η βάρκα μπορούν να φτάσουν μέχρι ενός σημείου. Ο ποταμός συμπεριφέρεται σαν μια λευκή τρύπα.
Ακολουθώντας το πνεύμα του παραδείγματος του W. Unruh, ο U. Leonhardt και ο συνεργάτης του P. Piwnicki υπέδειξαν έναν τρόπο να κατασκευαστούν οπτικές μαύρες τρύπες από τις οποίες είναι αδύνατον να ξεφύγει το φως (Leonhardt & Piwnicki, 1999). Αυτές οι διατάξεις, σύμφωνα με τις εκτιμήσεις των ερευνητών, θα μπορούσαν να αποτελέσουν ένα πειραματικό πεδίο για την κβαντική βαρύτητα, την προσπάθεια, δηλαδή, να παντρέψουμε την κβαντική μηχανική με την ΓΘΣ. Πρόκειται για ένα πρόβλημα που ταλανίζει την φυσική για δεκαετίες και το οποίο σχετίζεται άμεσα με την μεγάλη ενοποίηση όλων των δυνάμεων της φύσης. Οι μαύρες τρύπες απορροφούν το φως χάρις το πανίσχυρο βαρυτικό τους πεδίο. Σύμφωνα με τη ΓΘΣ, κάθε αντικείμενο με μάζα παραμορφώνει το χωροχρόνο κατά τέτοιο τρόπο, ώστε, κάθε τι που περνά από την γειτονιά του έλκεται προς το κέντρο της παραμόρφωσης, όπως ένα μπαλάκι του γκολφ όταν περνά από το χείλος μιας τρύπας. Το φως είναι η ταχύτερη οντότητα στο σύμπαν με ταχύτητα, στο κενό, ίση περίπου με 300,000 km/s. Συνεπώς, ακόμη και για μια μαύρη τρύπα, η σύλληψή του είναι μια αρκετά δύσκολη υπόθεση. Πως θα μπορούσε να γίνει κάτι τέτοιο στο εργαστήριο; Οι Leonhardt και Piwnicki σκέφθηκαν πως για να μπορέσουμε να συλλάβουμε το φως, θα έπρεπε πρώτα να το φρενάρουμε! Όπως είναι γνωστό, η ταχύτητα του φωτός είναι σταθερή στο κενό αλλά μεταβάλλεται όταν αυτό αναγκαστεί να ταξιδέψει μέσα σε ένα διαφανές υλικό μέσο (π.χ. νερό, γυαλί)[2]. Το 1999 η ομάδα της ερευνήτριας L. Hau, στο Rowland Institute of Science της Μασαχουσέτης και στο Πανεπιστήμιο Χάρβαρντ, κατόρθωσε να ελαττώσει την ταχύτητα του φωτός στο απίστευτο μέγεθος των 17 m/s. Αυτό έγινε δυνατόν όταν ανάγκασαν το φως να περάσει μέσα από μια ποσότητα από άτομα ρουβιδίου σε αέρια φάση, που είχαν προετοιμαστεί σε μια ειδική κατάσταση από πρόσθετες δέσμες λέιζερ (Hau et al, 1999). Λίγο αργότερα επιτεύχθηκε η επιβράδυνση του φωτός στα 0,5 m/s όταν αυτό πέρασε μέσα από ένα συμπύκνωμα Bose-Einstein (Hau, 2001).
Πως όμως μπορεί να επιβραδυνθεί το φως σε ένα κβαντικό αέριο; Τη λύση έχει δώσει η κβαντική μηχανική και ένα φαινόμενο που είναι γνωστό ως ηλεκτρομαγνητικά επαγόμενη διαφάνεια (electromagnetic induced transparency) (McCall & Hahn, 1969; Kocharovskaya & Khanin, 1986). Στην κβαντομηχανική όταν ένα φαινόμενο μπορεί να γίνει εφικτό μέσω δύο διαφορετικών ενδεχομένων αυτά μπορεί να συμβάλλουν ενισχυτικά ή καταστροφικά με τελικό αποτέλεσμα την μεγιστοποίηση ή το μηδενισμό της πιθανότητας εμφάνισης του φαινομένου αντίστοιχα. Ας δούμε μια τέτοια περίπτωση στο σχήμα της Εικ. 5. Ένα ηλεκτρόνιο μπορεί να βρεθεί σε μια ανώτερη ενεργειακή στάθμη |3> ξεκινώντας από την κατάσταση |1> με τη βοήθεια μιας δέσμης λέιζερ συχνότητας fp. Με τον ίδιο τρόπο μπορεί να βρεθεί στην κατάσταση |3> ξεκινώντας από μια άλλη κατάσταση |2> με τη βοήθεια μιας ασθενούς δέσμης λέιζερ συχνότητας fc. Η ασθενής αυτή δέσμη χρησιμοποιείται ουσιαστικά ως μια δέσμη ελέγχου. Όπως ήδη αναφέραμε, η κβαντική μηχανική προβλέπει πως τα δύο διαφορετικά ενδεχόμενα μέσω των οποίων μπορεί να βρεθεί το ηλεκτρόνιο στην ανώτερη ενεργειακά κατάσταση μπορεί να συμβάλλουν ενισχυτικά (οπότε μεγιστοποιείται η πιθανότητα το ηλεκτρόνιο να βρεθεί στην ανώτερη κατάσταση) ή καταστροφικά οπότε η άνοδος του ηλεκτρόνιου μπλοκάρεται και αυτό παραμένει στις χαμηλώτερες καταστάσεις. Ρυθμίζοντας κατά βούληση τη συχνότητα και την ένταση της ασθενούς δέσμης λέιζερ μπορούμε να επιτύχουμε οποιαδήποτε από τις δύο καταστάσεις ή κάποια ενδιάμεση όπου το ηλεκτρόνιο διεγείρεται μερικώς και μπορεί να βρεθεί ταυτόχρονα τόσο στην ανάωτερη κατάσταση όσο και στις δύο χαμηλώτερες (η κβαντική τα επιτρέπει αυτά…).
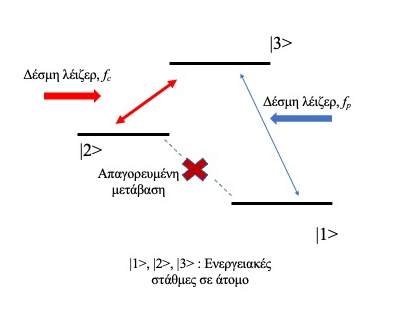
Εικόνα 5: Ένα ηλεκτρόνιο μπορεί να βρεθεί σε μια ανώτερη ενεργειακή στάθμη |3> ξεκινώντας από την κατάσταση |1> με τη βοήθεια μιας δέσμης λέιζερ συχνότητας fp. Με τον ίδιο τρόπο μπορεί να βρεθεί στην κατάσταση |3> ξεκινώντας από μια άλλη κατάσταση |2> με τη βοήθεια μιας ασθενούς δέσμης λέιζερ συχνότητας fc. Η κβαντική μηχανική προβλέπει πως τα δύο διαφορετικά ενδεχόμενα μέσω των οποίων μπορεί να βρεθεί το ηλεκτρόνιο στην ανώτερη ενεργειακά κατάσταση μπορεί να συμβάλλουν ενισχυτικά (οπότε μεγιστοποιείται η πιθανότητα το ηλεκτρόνιο να βρεθεί στην ανώτερη κατάσταση) ή καταστροφικά οπότε η άνοδος του ηλεκτρόνιου μπλοκάρεται και αυτή παραμένει στις χαμηλώτερες καταστάσεις. Στη βιβλιογραφία το παραπάνω σχήμα είναι γνωστό ως «σχηματισμός-Λ» (Λ-configuration).
Όταν το ηλεκτρόνιο βρεθεί στην ανώτερη κατάσταση έχει απορροφήσει ουσιαστικά ενέργεια από την βασική δέσμη λέιζερ. Άρα η δέσμη αυτή ουσιαστικά συμπεριφέρερται σαν να έχει ταξιδέψει μέσα σε ένα υλικό με κάποιο δείχτη διάθλασης. Όταν το ηλεκτρόνιο εγκλωβίζεται στις χαμηλές καταστάσεις τότε ουσιαστικά δεν μπορεί να απορροφήσει ενέργεια από τη δέσμη λέιζερ η οποία συνεχίζει την πορεία της απρόσκοπτα σαν να ταξιδεύει στο κενό. Το παραπάνω σύστημα είναι στην ουσία ένα υλικό όπου ο δείχτης διάθλασής του, ως προς την κύρια δέσμη, μπορεί να μεταβληθεί κατά βούληση.
‘Όπως έχουν υποδείξει οι Leonhardt και Piwnicki, όταν ένα μέσο, όπως ένα συμπύκνωμα Bose-Einstein, που επιβραδύνει το φως μετακινηθεί, τότε μπορεί να παρασύρει το φως μαζί του. Το φως έχοντας να αντιμετωπίσει ένα γρήγορο «άνεμο» προς τα εμπρός, θα υστερήσει και θα μείνει πίσω. Οι δύο επιστήμονες πιστεύουν ότι αν κατασκεύαζαν έναν περιστρεφόμενο στρόβιλο σε ένα μέσο, σαν αυτά που χρησιμοποίησε η Len Hau, αυτός θα “κατάπινε” το φως. Πράγματι, τα πιο συγγενή πράγματα προς τις μαύρες τρύπες που έχουμε στη Γη είναι οι στρόβιλοι. Οι τυφώνες, για παράδειγμα, ρουφούν δέντρα, στέγες και φορτηγά. Η δύναμή τους προέρχεται από την χαμηλή πίεση στο κέντρο του στροβίλου σε σχέση με την πίεση στην περιφέρεια του. Σύμφωνα με τους υπολογισμούς των δύο επιστημόνων ένας στρόβιλος μπορεί να ασκήσει μιαν ανάλογη επίδραση στο φως. Εάν ο στρόβιλος περιστρέφεται πολύ πιο γρήγορα από ότι μπορεί να κινηθεί το φως, κάθε ακτίνα που περνά πολύ κοντά από το κέντρο του θα συλληφθεί και θα συρθεί προς αυτό. To φως, τελικά, θα απορροφηθεί από το στρόβιλο. Οπότε, ακριβώς όπως στην περίπτωση μιας πραγματικής μαύρης τρύπας, ο στρόβιλος έχει έναν ορίζοντα γεγονότων πέρα από τον οποίο η απόδραση του φωτός είναι αδύνατη.
ΑΚΤΙΝΟΒΟΛΙΑ HAWKING ΣΤΟ ΕΡΓΑΣΤΗΡΙΟ
Ο U. Leonhardt υποστηρίζει πως σε μια οπτική μαύρη τρύπα το φως συμπεριφέρεται σαν να βρίσκεται εντός ενός πολύ ισχυρού βαρυτικού πεδίου. Το φως, όταν βρεθεί μέσα στο περιστρεφόμενο αέριο μιας οπτικής μαύρης τρύπας, κινείται εντός ενός καμπύλου χωροχρόνου και αυτό το γεγονός μπορεί να αξιοποιηθεί για να ελεγχθούν, σε πρώτη φάση, προβλέψεις που αφορούν σε κβαντικά φαινόμενα που εκδηλώνονται σε ισχυρά βαρυτικά πεδία (Drori et al, 2019). Η πιο διάσημη από αυτές διατυπώθηκε το 1975 όταν ο S. Hawking απέδειξε ότι οι μαύρες τρύπες ακτινοβολούν (Hawking, 1975). Σύμφωνα με την κβαντική θεωρία πεδίου, σε μια μαύρη τρύπα, ζεύγη στοιχειωδών σωματιδίων αναδύονται από το κενό και στην συνέχεια ανασυνδυάζονται και εξαφανίζονται. Αυτά τα «εν δυνάμει» σωματίδια δεν μπορούν να επιβιώσουν για πολύ χρόνο. Εάν, όμως, το ζεύγος σωματιδίων τύχει να γεννηθεί μόλις πάνω από τον ορίζοντα γεγονότων μιας μαύρης τρύπας, η βαρύτητα μπορεί να διαχωρίσει το ζεύγος σωματιδίων. Ένα από τα δύο σωμάτια πέφτει στην τρύπα ενώ το άλλο “κερδίζει” κάποια ενέργεια και διαφεύγει. Αυτά τα διαφυγόντα σωματίδια συνιστούν την περίφημη ακτινοβολία Hawking, η οποία δεν έχει καταγραφεί πειραματικά μέχρι σήμερα σε αστροφυσικό περιβάλλον (Εικ.6).
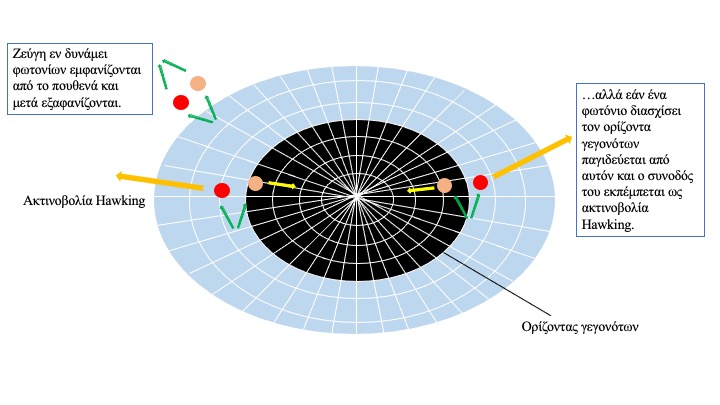
Εικόνα 6: Η γένεση της ακτινοβολίας Hawking. Σε μια μαύρη τρύπα, ζεύγη στοιχειωδών σωματιδίων αναδύονται από το κενό και στην συνέχεια ανασυνδυάζονται και εξαφανίζονται. Εάν το ζεύγος σωματιδίων τύχει να γεννηθεί μόλις πάνω από τον ορίζοντα γεγονότων μιας μαύρης τρύπας, η βαρύτητα μπορεί να το διασπάσει. Ένα από τα δύο σωμάτια πέφτει στην τρύπα ενώ το άλλο “κερδίζει” κάποια ενέργεια και διαφεύγει. Αυτά τα διαφυγόντα σωματίδια συνιστούν την περίφημη ακτινοβολία Hawking.
Το όλο θέμα έχεις και άλλες, ακόμη πιο εξωτικές, προεκτάσεις. Μια από τις πιο παράδοξες προβλέψεις για τις μαύρες τρύπες είναι η δυνατότητα παραγωγής ακτινοβολίας λέιζερ από αυτές (Corley & Jacobson, 1999). Στην κοσμολογία προβλέπεται πως κάτι τέτοιο μπορεί να συμβεί στην περίπτωση που η μαύρη τρύπα είτε περιστρέφεται είτε φέρει ηλεκτρικό φορτίο. Μια τέτοια μαύρη τρύπα χαρακτηρίζεται από την ύπαρξη δύο οριζόντων γεγονότων, έναν εσωτερικό και έναν εξωτερικό, οι οποίοι διαμορφώνουν μια γιγάντια οπτική κοιλότητα (Εικ.7). Τα φωτόνια που πέφτουν στη μαύρη τρύπα φτάνουν στον εσωτερικό ορίζοντα. O ορίζοντας αυτός είναι ένας ορίζοντας μιας λευκής τρύπας που ανακλά τα πάντα προς τον εξωτερικό ορίζοντα γεγονότων. Αυτές οι ανακλάσεις οδηγούν στο σχηματισμό ενός στάσιμου κύματος. Κατά τη διάρκεια αυτών των ανακλάσεων η ενέργειά των φωτονίων ελλατώνεται καθώς ένα μέρος αυτής θα εκπέμπεται εκτός του ορίζοντα γεγονότων, με τη μορφή φωτός, σε μια κοινή συχνότητα και με συνεχώς αυξανόμενη ένταση, σχηματίζοντας μια δέσμη λέιζερ. Είναι ενδιαφέρον πως η ενίσχυση αφορά όχι μόνο φωτόνια αλλά εν γένει κάθε μποζονικό σωματίδιο ενώ στην περίπτωση φερμιονίων το φαινόμενο αντιστρέφεται και έχουμε εξασθένηση της ακτινοβολίας Hawking.
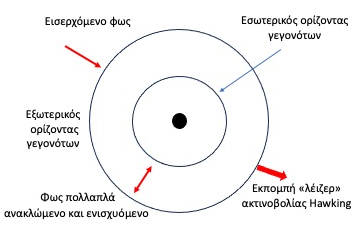
Εικόνα 7: Μια μαύρη με δύο οριζόντες γεγονότων, έναν εσωτερικό και έναν εξωτερικό, οι οποίοι διαμορφώνουν μια γιγάντια οπτική κοιλότητα. Τα φωτόνια που πέφτουν στη μαύρη τρύπα φτάνοντας στον εσωτερικό ορίζοντα ανακλώνται προς τον εξωτερικό ορίζοντα γεγονότων. Αυτές οι ανακλάσεις οδηγούν στο σχηματισμό ενός στάσιμου κύματος. Κατά τη διάρκεια αυτών των ανακλάσεων η ενέργειά των φωτονίων ελλατώνεται καθώς ένα μέρος αυτής θα εκπέμπεται εκτός του ορίζοντα γεγονότων, με τη μορφή φωτός, σε μια κοινή συχνότητα και με συνεχώς αυξανόμενη ένταση, σχηματίζοντας μια δέσμη λέιζερ.
Η προσομοίωση αυτού του φαινόμενου έχει γίνει με τη βοήθεια ενός συμπυκνώματος Bose-Einstein από τον J. Steinhauer στο Πολυτεχνείο Technion στο Ισραήλ και θα μπορούσε να προσφέρει ισχυρά αποδεικτικά στοιχεία για την ύπαρξη της ακτινοβολίας Hawking (Steinhauer, 2014). Το σύστημα λειτούργησε για την ενίσχυση ηχητικών κυμάτων και όχι φωτός και παρόλο που δεν συνιστά μια πραγματική βαρυτική μαύρη τρύπα, το πείραμα, εντούτοις, παρείχε ισχυρές ενδείξεις πως ο μηχανισμός Hawking λειτουργεί, ενδεικτικό του είδους των πληροφοριών που μπορεί να αποκομίσει κανείς από μικρής κλίμακας προσομειώσεις βαρυτικών φαινομένων χρησιμοποιώντας μεθόδους της οπτικής ή της ακουστο-οπτικής. Αξίζει να σημειωθεί πως πρόσφατα ένας ερευνητής, ο H. Katayama, κατόρθωσε να προσομοιώσει αυτό το φαινόμενο με τη βοήθεια ενός σολιτονίου (soliton) που αναπτύχθηκε σε ένα υπεραγώγιμο ηλεκτρικό κύκλωμα (Katayama, 2021).
ΠΡΟΣΟΜΟΙΩΣΕΙΣ ΤΗΣ ΔΥΝΑΜΙΚΗΣ ΤΟΥ ΣΥΜΠΑΝΤΟΣ
Ιδιαίτερα εντυπωσιακό είναι το γεγονός πως τα κβαντικά αέρια μπορούν να αξιοποιηθούν ως πλατφόρμες προσομοίωσης φαινομένων κοσμικής κλίμακας όπως η ίδια η δημιουργία του Σύμπαντος. Δεδομένου ότι κάθε φορά που οι επιστήμονες παρατηρούν τον ουρανό βλέπουν πίσω στο παρελθόν αναρωτιέται κάποιος γιατί χρειάζεται να καταφύγουμε σε προσομοιώσεις για τη διερεύνηση κοσμολογικών φαινομένων. Η απάντηση βρίσκεται στο γεγονός πως υπάρχει ένα όριο στο παρελθόν πέρα από το οποίο δεν μπορούμε να διεισδύσουμε. Σύμφωνα με την εκδοχή της θεωρίας της Μεγάλης Έκρηξης (Big Bang Theory) οι πρώτες «στιγμές» (κάπου 380.000 χρόνια!) μετά την έκρηξη, που είναι στην κυριολεξία πολύ κρίσιμες για την μετέπειτα εξέλιξη του Σύμπαντος, καλύπτονται από ένα πέπλο μυστηρίου. Κατά την περίοδο αυτή ο συμπαντικός χώρος εικάζεται πως ήταν γεμάτος από πυκνό πλάσμα το οποίο είναι μη διαπερατό στην ηλεκτρομαγνητική ακτινοβολία με αποτέλεσμα αυτή να μην κατορθώσει να ταξιδέψει στο χωροχρόνο και να φτάσει σήμερα στα όργανα παρατήρησης που διαθέτουμε. Μια προσπάθεια να φωτιστεί αυτή η αρχική περίοδος έχει γίνει στα πλαίσια της Θεωρίας του Πληθωρισμού (Inflation Theory), η οποία προτείνει ότι ο χώρος στην αρχή επεκτάθηκε ταχύτατα (σε χρόνο 10-30 s το μέγεθος του Σύμπαντος διπλασιάστηκε εκατό φορές!) για να ακολουθήσει μια δραματική επιβράδυνση. Αλλά δεν είναι γνωστό με βεβαιότητα εάν η θεωρία είναι σωστή, και ακόμα κι αν είναι, πολλές λεπτομέρειες μένουν να διερευνηθούν. Οι κοσμολόγοι δεν μπορούν να ταξιδέψουν, μέσω παρατηρήσεων, τόσο πίσω στο χρόνο ώστε έχουν μια εικόνα του τι συνέβη κατά την εποχή του πληθωρισμού. Μια λύση σε αυτό το πρόβλημα είναι να καταφύγουμε στην προσομοίωση του φαινομένου και εδώ τα κβαντικά αέρια έχουν αφήσει πολλές υποσχέσεις.
Πριν λίγα χρόνια η ερευνητική ομάδα του G. Campbell, στο Πανεπιστήμιο του Maryland στις ΗΠΑ, έδειξε πως η ταχύτατη διαστολή ενός παγιδευμένου συμπυκνώματος Bose-Einstein παρουσιάζει παρόμοια χαρακτηριστικά με ένα διαστελλόμενο σύμπαν (Eckel, 2018). Η ομάδα αυτή κατόρθωσε να παγιδεύσει ένα τέτοιο συμπύκνωμα από εκατοντάδες άτομα σε μια δαχτυλιοειδή παγίδα της οποίας η ακτίνα τετραπλασιάστηκε μέσα σε μερικά χιλιοστά του δευτερολέπτου. Τα αποτελέσματα του πειράματος έδειξαν μια αξιοσημείωτη αναλογία ανάμεσα στη δυναμική του διαστελλόμενου συμπυκνώματος και αυτήν ενός διαστελλόμενου σύμπαντος.
Μόλις το 2022 η ερευνητική ομάδα του M. Oberthaller, στο Πανεπιστήμιο της Χαϊδελβέργης, έκανε ένα σημαντικό βήμα στην προσομοίωση της διαστολής του Σύμπαντος κατασκευάζοντας μια πειραματική πλατφόρμα στην οποία μπορεί να διερευνηθεί αυτή η κατάσταση, σε ένα κβαντικό αέριο από άτομα καλίου το οποίο προσομοίωνε το σύμπαν. Η πυκνότητα του, μάλιστα, σχετίζεται με την καμπυλότητα του σύμπαντος. Το νέο ποιοτικό στοιχείο που έφερε αυτό το πείραμα ήταν πως αντί οι ερευνητές να αφήσουν το κβαντικό αέριο να διασταλεί στο χώρο και το χρόνο προσομοίωσαν μια κατάσταση διαστολής ενώ τα άτομα παρέμεναν στη θέση τους. Πως έγινε κάτι τέτοιο εφικτό; Με μια απλή σκέψη: τα μέρη ενός συστήματος που διαστέλλεται αλληλεπιδρούν με δυνάμεις που διαρκώς εξασθενούν. Αν σε ένα κβαντικό αέριο εφαρμόσουμε ένα εξωτερικό μαγνητικό πεδίο του οποίου μεταβάλουμε την ένταση μπορούμε να ελαττώνουμε κατά βούληση τις αλληλεπιδράσεις μεταξύ των ατόμων του αερίου και έτσι να προσομοιώσουμε μια κατάσταση διαστολής (Viermann et al, 2022). Για να επιτευχθεί πειραματικά αυτή η κατάσταση οι ερευνητές αξιοποίησαν ένα φαινόμενο της ατομικής φυσικής γνωστό ως συντονισμός Feshbach (Feshbach resonance). Τα αποτελέσματα του πειράματος αυτού είναι πάρα πολύ ενθαρρυντικά καθώς επιβεβαίωσαν μια σημαντική ιδιότητα που έχει ένα διαστελλόμενο σύμπαν. Πράγματι, μια απλή πρόβλεψη της κβαντικής θεωρίας πεδίου είναι πως σε ένα διαστελλόμενο σύμπαν οι κβαντικές διακυμάνσεις οδηγούν στο σχηματισμό ζευγών σωματιδίων-αντισωματιδίων. Κάτι τέτοιο είναι αδύνατο σε ένα στατικό σύμπαν. Σε ένα διαστελλόμενο κβαντικό αέριο τα αντίστοιχα σωματίδια θα ήταν φωνόνια και αυτό ήταν ακριβώς που παρατήρησαν ο Oberthaller και οι συνεργάτες του. Οι τροχιές τους μάλιστα καθορίζονται από την καμπυλότητα του χωροχρόνου μέσα στον οποίο κινούνται. Μελετώντας αυτές τις τροχιές οι ερευνητές ήταν σε θέση να επιβεβαιώσουν ότι το προσομοιούμενο σύμπαν είχε την επιθυμητή καμπυλότητα. Παράλληλα οι ερευνητές προχώρησαν και σε προσομοίωση διαφορετικών τύπων διαστολής, με σταθερό, με επιβραδυνόμενο και με επιταχυνόμενο ρυθμό αντίστοιχα. Και στις τρεις περιπτώσεις μετά το πέρας της διαστολής το κβαντικό αέριο είχε κυριευθεί από ακουστικά κύματα παρόμοια με αυτά που κυριαρχούσαν στο Σύμπαν την εποχή του πλάσματος. Οι επιστήμονες πλέον έχουν θέσει επί τάπητος το φιλόδοξο σχέδιο να χρησιμοποιήσουν αυτού του είδους τις προσομοιώσεις ώστε να διερευνήσουν τη δυναμική του Σύμπαντος πριν την εποχή του πληθωρισμού.
Τέλος αξίζει να αναφέρουμε και την αξιοποίηση των οπτικών κρυστάλλων ατόμων σε προσομοιώσεις της μεταβολής της κβαντικής φάσης που εικάζεται πως συνέβη στα πρώτα στάδια του σύμπαντος. Η πιο πρόσφατη προσπάθεια σε αυτή την κατεύθυνση έγινε από τον Bo Song και τους συνεργάτες του στο Πανεπιστήμιο του Cambridge οι οποίοι αξιοποίησαν παγιδευμένα άτομα σε οπτικά πλέγματα και παρατήρησαν για πρώτη φορά ασυνεχείς μεταβάσεις από καταστάσεις μονωτή Mott σε μια υπερρευστη κατάσταση υψηλότερης ενέργειας στην οποία τα άτομα μπορούν να μετακινηθούν ελεύθερα μεταξύ διαφορετικών τοποθεσιών μέσα στο πλέγμα (Song et al, 2022). Οι ασυνεχείς μεταβάσεις φάσεως έχουν σχέση με τις μεταβολές φάσεως στην αρχή δημιουργίας του Σύμπαντος. Στο εν λόγω πείραμα επιτεύχθηκαν με διαταραχή του οπτικού κρύσταλλου.
ΕΠΙΛΟΓΟΣ
Τα κβαντικά αέρια φαίνεται να αποτελούν μια πολλά υποσχόμενη πλατφόρμα προσομοίωσης κοσμολογικών φαινομένων μεγάλης κλίμακας. Με τη βοήθειά τους οι ερευνητές προσπαθούν να ρίξουν φως σε δυσεπίλυτα ερωτήματα που αφορούν στη δυναμική αυτών των φαινομένων. Αρκετοί από αυτούς θεωρούν πως όλη αυτή η ερευνητική προσπάθεια μπορεί να συμβάλλει καθοριστικά σε έναν άλλο, διακαή, πόθο της φυσικής: την ενοποίηση της κβαντομηχανικής με τη βαρύτητα. Εν κατακλείδι, θα πρέπει να σημειωθεί πως τα κβαντικά αέρια δεν συνιστούν τα μόνα φυσικά συστήματα στα οποία επιχειρούνται προσομοιώσεις κοσμολογικών φαινομένων (Novello et al, 2002).
ΕΥΧΑΡΙΣΤΙΕΣ
Ευχαριστούμε τον Απόστολο Κυριαζή για την ευγενική παραχώρηση της κεντρικής φωτογραφίας του άρθρου. Οι Εικόνες 3 και 4 αποτελούν καλλιτεχνική προσαρμογή εικόνων από το σύνδεσμο από το άρθρο https://skullsinthestars.com/2008/03/12/making-optical-blackholes-in-a-laboratory/. Η προσαρμογή έγινε από τον ζωγράφο Παναγιώτη (Τάκη) Βαρελά, μέλος του ΔΣ του Εθνικού Μουσείου Σύγχρονης Τέχνης (ως εκπρόσωπος του Επιμελητήριου Εικαστικών Τεχνών Ελλάδας) για την έκδοση του βιβλίου Taming Atoms: The Renaissance of Atomic Physics, (Lembessis, 2020).
ΒΙΒΛΙΟΓΡΑΦΙΑ
Chen, Η., Chan, C., T., and P. Sheng, 2010. Transformation optics and metamaterials. Nature Materials 9, 387-396. DOI: 10.1038/nmat2743
Corley, S., and Jacobson, T., 1999. Black hole lasers. Phys. Rev. D. 124011. https://doi.org/10.1103/PhysRevD.59.124011
Dolin, L., S., 1961. To the possibility of comparison of three-dimensional electromagnetic systems with nonuniform anisotropic filling. Izvestiya Vuzov. Radiophizika 4, 964-967. https://www.math.utah.edu/~milton/DolinTrans2.pdf
Drori, J., Rosenberg, Y., Bermudez, D., Silberberg, Y., and Leonhardt, U., 2019. Observation of Stimulated Hawking Radiation in an Optical Analogue. Phys. Rev. Lett. 122, 010404. https://doi.org/10.1103/PhysRevLett.122.010404
Eckel, S., Kumar, A., Jacobson, T., Spielman, I., B., and Campbell, G., K., 2018. A Rapidly Expanding Bose-Einstein Condensate: An Expanding Universe in the Lab. Phys. Rev. X 8, 021021. https://doi.org/10.1103/PhysRevX.8.021021
Euvé, L.-P., Michel, F., Parentani, R., Philbin, T., G., and Rousseaux, G., 2016. Observation of Noise Correlated by the Hawking Effect in a Water Tank. Phys. Rev. Lett. 117, 121301. https://doi.org/10.1103/PhysRevLett.117.121301
Greenleaf, A., Lassas, M., and Uhlmann, G., 2003. Anisotropic conductivities that cannot be detected by EIT. Physiol. Meas. 24, 413-419. DOI: 10.1088/0967-3334/24/2/353
H. Fizeau, H., 1851. Sur les hypotheses relatives a l’ether lumineux, et sur une experience qui parait demontrer que le mouvement des corps change la vitesse avec laquelle la lumiere se propage dans leur interieur. Comptes Rendus de l’Académie des Sciences 33, 349-355. https://www.academie-sciences.fr/pdf/dossiers/Fizeau/Fizeau_pdf/CR1851_p349.pdf
Fresnel, A., J., 1818. Lettre de M. Fresnel à M. Arago, sur l’ influence du movement terrestre dans quelques phénomènes d’ optique. Ann. Chim. Phys. 8, 57-66.
Gordon, W., 1923. Zur Lichtfortpflanzung nach der Relativitätstheorie,” (For the propagation of light according to the Theory of Relativity). Ann. Phys. (Leipzig) 72, 421-456. http://www.neo-classical-physics.info/uploads/3/4/3/6/34363841/gordon_-_optical_metrics.pdf
Hau, L., V., Harris, S., E., Dutton, Z., and Behroozi, C., H., 1999. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 397, 594-598. https://doi.org/10.1038/17561
Hau, L., V., 2001. Frozen Light. Scientific American, July Issue, 44-51. https://www.scientificamerican.com/article/frozen-light/
Hawking, S., W., 1975. Particle creation by black holes. Commun.Math.Phys. 43, 199-220. https://doi.org/10.1007/BF02345020
Katayama, H., 2021. Quantum-circuit black hole lasers. Scientific Reports, 11, 19137. https://doi.org/10.1038/s41598-021-98456-0
Kocharovskaya, O., Khanin, Ya., I., 1986. Sov. Phys. JETP, 63, 945. http://jetp.ras.ru/cgi-bin/dn/e_063_05_0945.pdf
Lembessis, V. E., 2020. Taming Atoms: The Renaissance of Atomic Physics. Bellingham, Washington USA: SPIE. https://spie.org/Publications/Book/2563827?SSO=1
Leonhardt, U., and Piwnicki, P., 1999. Relativistic Effects of Light in Moving Media with Extremely Low Group Velocity. Phys. Rev. Lett. 84, 822-825. https://doi.org/10.1103/PhysRevLett.84.822
Leonhardt, U., and Philbin, T., G., 2006. General relativity in electrical engineering. New J. Phys. 8, 247-266. https://doi.org/10.1088/1367-2630/8/10/247
Leonhardt, U., and Philbin, T., 2010. GEOMETRY AND LIGHT: THE SCIENCE OF INVISIBILITY. New York: Dover. https://store.doverpublications.com/0486476936.html
Lorentz, H., A., 1895. Versuch einer Theorie der elektrischen und
optischen Erscheinungen von bewegten Körpern (Attempt of a Theory of Electrical and Optical Phenomena
in Moving Bodies). Leiden: Brill (1895), p.31. https://en.wikisource.org/wiki/Translation:Attempt_of_a_Theory_of_Electrical_and_Optical_Phenomena_in_Moving_Bodies
McCall, S., L., and Hahn, E., L., 1969. Self-Induced Transparency. Phys. Rev. 183, 457. https://doi.org/10.1103/PhysRev.183.457
Muñoz de Nova, J., R., Golubkov, K., Kolobov, V., I., and Steinhauer, J., 2019. Observation of thermal Hawking radiation and its temperature in an analogue black hole. Nature 569, 688–691. DOI: 10.1038/s41586-019-1241-0
Novello, M., Visser, M., Volovik, G., 2002. Artificial Black Holes. Singapore: World Scientific Publishing. https://www.worldscientific.com/worldscibooks/10.1142/4861#t=aboutBook
Plebanski, J., 1960. Electromagnetic Waves in Gravitational Fields. Phys. Rev. 118, 1396-1408. https://doi.org/10.1103/PhysRev.118.1396
Rytov, S., M., 1938. On the transition between wave and geometric optics. Compt. Rend. (Doklady) Acad. Sci. USSR 18, 263-266.
Song, B., Dutta, S., Bhave, S., Yu, Jr.-C., Carter, E., Cooper., N., and Schneider, U., 2022. Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. Nature Physics, 259-264. https://doi.org/10.1038/s41567-021-01476-w
Steinhauer, J., 2014. Observation of self-amplifying Hawking radiation in an analogue black-hole laser. Nature Physics 10, 864-869. https://doi.org/10.1038/nphys3104
Tamm, I., Y., 1924. The electrodynamics of anisotropic media in the special theory of relativity. J. Russ. Phys.-Chem. Soc. 56, 2-3, 248-262. http://neo-classical-physics.info/uploads/3/4/3/6/34363841/tamm_-_ed_of_anisotropic_media_1924.pdf
Unruh, W., G., 1981. Experimental Black-Hole Evaporation? Phys. Rev. Lett. 46, 1351-1353. https://doi.org/10.1103/PhysRevLett.46.1351
Viermann, C., Sparn, M., Liebster, N., Hans, M., Kath, E., Parra-López, A., Tolosa-Simeón, M., Sánchez-Kunz, N., Haas, T., Strobel, H., Floerchinger, S., and Oberthaler, M., K., 2022. Nature 611, 260-264. https://doi.org/10.1038/s41586-022-05313-9
White, R., 1973. Acoustic ray tracing in moving inhomogeneous fluids. J. Acoust. Soc. Amer. 53, 1700-1704. https://doi.org/10.1121/1.1913522
Zeeman, P., 1914. Fresnel’s coefficient for light of different colours,” Proc. R. Acad. Amsterdam 17, 445-451. https://dwc.knaw.nl/DL/publications/PU00012688.pdf





