
Στο πρώτο άρθρο του αφιερώματος στους οπτικούς κρυστάλλους παρουσιάσαμε τον τρόπο κατασκευής τους, τις ιδιότητές τους και τις ποικιλίες στις οποίες εμφανίζονται. Σε αυτό το άρθρο εστιάζουμε στις πιο σημαντικές εφαρμογές τους.
ΠΡΟΣΟΜΟΙΩΣΕΙΣ ΦΑΙΝΟΜΕΝΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
Στην επιστημονική έρευνα είναι συνήθης πρακτική η προσομοίωση πολύπλοκων φυσικών συστημάτων από ηλεκτρονικούς υπολογιστές, όταν η αναλυτική περιγραφή τους είναι είτε αδύνατη είτε εξαιρετικά δύσκολη. Στην περίπτωση των κβαντικών συστημάτων, η προσομοίωση, ακόμη και των πιο απλών από αυτά, είναι σχεδόν αδύνατη και μπορεί να προκαλέσει σημαντικά προβλήματα λειτουργίας ακόμη και στα πιο ισχυρά υπολογιστικά συστήματα που διαθέτουμε. Το ζήτημα της κβαντικής προσομοίωσης τέθηκε για πρώτη φορά το 1982 από τον R. Feynmann, o οποίος υπέδειξε πως, σε κάποιες περιπτώσεις, θα ήταν δυνατόν να βρεθεί ένα απλούστερο, και πειραματικά πιο προσιτό κβαντικό σύστημα, το οποίο να «μιμείται» τη συμπεριφορά του κβαντικού συστήματος που ενδιαφερόμαστε να μελετήσουμε (Feynman, 1982). Οι κβαντικές προσομοιώσεις συνιστούν ένα από τα πιο ραγδαία εξελισσόμενα και, συνάμα, συναρπαστικά πεδία έρευνας στην ατομική φυσική του 21ου αιώνα. Οι οπτικοί κρύσταλλοι ατόμων προσφέρουν ένα ιδανικό περιβάλλον για την προσομοίωση αρκετών κβαντικών φαινομένων. Οι περισσότερες από τις εφαρμογές τους, που παρουσιάζουμε στη συνέχεια, είναι προσομοιώσεις φαινομένων που απαντώνται στη φυσική της συμπυκνωμένης ύλης.
Μια από τις πρώτες εφαρμογές των οπτικών πλεγμάτων ήταν η προσομοίωση των ταλαντώσεων Bloch. Πρόκειται για τις ταλαντώσεις των ελεύθερων ηλεκτρονίων ενός μετάλλου που εμφανίζονται όταν εφαρμόσουμε σε αυτό ένα ομογενές ηλεκτρικό πεδίο. Τα ηλεκτρόνια δέχονται μια σταθερή δύναμη από το ηλεκτρικό πεδίο αλλά, προς έκπληξή μας, αντί να επιταχυνθούν ομαλά, εκτελούν μια ταλαντωτική κίνηση. Η προσομοίωση αυτού του φαινόμενου γίνεται με την παγίδευση ατόμων σε ένα μονοδιάστατο οπτικό κρύσταλλο, σαν αυτό που περιγράψαμε στο προηγούμενο άρθρο. Όπως έχουμε αναφέρει, όταν αυξήσουμε τη συχνότητα ενός από τα δύο λέιζερ, ο κρύσταλλος μετατρέπεται σε οπτικό ιμάντα. Αν η αύξηση της συχνότητας είναι γραμμική με το χρόνο, τότε ο ιμάντας επιταχύνεται στο χώρο και μαζί με αυτόν τα παγιδευμένα άτομα. Στο σύστημα αναφοράς του ιμάντα αυτό ισοδυναμεί με την επίδραση στο άτομο μιας σταθερής αδρανειακής δύναμης ταυτόχρονα με την περιοδική δύναμη που του ασκεί το οπτικό πλέγμα. Στην ουσία το κάθε άτομο συμπεριφέρεται σαν ένα ηλεκτρόνιο που κινείται στο περιοδικό δυναμικό ενός στερεού κρυστάλλου υπό την επίδραση ενός ομογενούς ηλεκτρικού πεδίου. Το φαινόμενο αυτό παρατηρήθηκε το 1996 σε άτομα παγιδευμένα μέσα σε ένα στάσιμο κύμα λέιζερ (Ben Dahan et al, 1996). Στο πείραμα αυτό καταγράφηκαν οι περιοδικές μεταβολές της ορμής που αποτελούν ένδειξη της ταλάντωσης. Η απευθείας παρατήρηση των ταλαντώσεων των ατόμων στο χώρο έγινε πρόσφατα σε άτομα παγιδευμένα σε οπτικό κρύσταλλο (Geiger et al, 2018).
Στην κβαντική φυσική τα μονοδιάστατα συστήματα χαρακτηρίζονται από κάποιες εντυπωσιακές και σε πρώτη ανάγνωση “παράδοξες” ιδιότητες. Για παράδειγμα, οι διαστάσεις ενός μακροσκοπικού κβαντικού συστήματος παίζουν κρίσιμο ρόλο στη φυσική του συμπεριφορά. Μέχρι πρόσφατα η πειραματική δραστηριότητα σε αυτό το πεδίο ήταν περιορισμένη. Σήμερα είμαστε σε θέση να κατασκευάζουμε διατάξεις από μονοδιάστατα κβαντικά αέρια χρησιμοποιώντας οπτικά πλέγματα δύο διαστάσεων. Σε αυτές τις δομές τα άτομα παγιδεύονται σε περιοχές με σωληνοειδή μορφή και μπορούν να κινηθούν μόνο κατά μήκος αυτών.
Το 1960 ο M. Girardeau ανακάλυψε πως, όταν περιορίσουμε σε μια διάσταση ένα σύνολο από μποζόνια, η συμπεριφορά τους είναι ισοδύναμη με ένα σύνολο από φερμιόνια που δεν αλληλεπιδρούν μεταξύ τους. Αυτό το αξιοσημείωτο φαινόμενο είναι γνωστό στη φυσική με τον όρο φερμιονιοποίηση (fermionization) (Girardeau, 1960). Η φερμιονιοποίηση εμφανίζεται όταν οι απωστικές δυνάμεις μεταξύ των ατόμων γίνονται πολύ ισχυρές. Τα άτομα, τότε, τείνουν να διαχωριστούν κατά μήκος του άξονα του παγιδευτικού σωλήνα και η πιθανότητα να βρεθούν στην ίδια θέση μηδενίζεται. Με αυτόν τον τρόπο τα άτομα, στην πράξη, “μιμούνται” την Απαγορευτική Αρχή του Pauli: τα μποζόνια συμπεριφέρονται ως φερμιόνια. Η πρώτη πειραματική επιβεβαίωση της φερμιονιοποίησης ενός συνόλου μποζονίων παρατηρήθηκε από την ομάδα του W. Phillips στο NIST (Fertig et al, 2005). Όταν οι αλληλεπιδράσεις μεταξύ των ατόμων σε μονοδιάστατα κβαντικά συστήματα γίνουν ακόμη ισχυρότερες θα μπορούσαμε να φτάσουμε σε ένα αέριο Tonks–Girardeau όπου η φερμιονιοποίηση είναι ακόμη ισχυρότερη (Tonks, 1936). Στην περίπτωση που αυτό επιτευχθεί, θα έχουμε κατορθώσει κάτι πραγματικά εκπληκτικό: ένα σύστημα μποζονίων που μπορεί να περιγραφεί από τη θεωρία των ελεύθερων φερμιονίων. Η παρατήρηση αυτού του φαινόμενου αποτελεί μια από τις πιο μεγάλες προκλήσεις για την πειραματική ατομική φυσική.
ΜΕΤΑΒΟΛΕΣ ΚΒΑΝΤΙΚΩΝ ΦΑΣΕΩΝ
Το 1998 ο P. Zoller και οι συνεργάτες του στο Πανεπιστήμιο του Innsbruck απόδειξαν πως αν μεταφέρουμε ένα συμπύκνωμα Bose-Eistein σε έναν οπτικό κρύσταλλο τότε μπορούμε να παρατηρήσουμε μια πολύ ενδιαφέρουσα μεταβολή φάσης. Το υπερρευστό συμπύκνωμα μετατρέπεται σε «μονωτή». Δηλαδή τα άτομα δεν μπορούν πλέον να κινούνται ελεύθερα στο «πλέγμα» του οπτικού κρυστάλλου και παγιδεύονται σε συγκεκριμένες θέσεις σε αυτό. Πρόκειται για μια μεταβολή φάσης που είναι γνωστή στη βιβλιογραφία ως μετάβαση Mott (Jaksch et al, 1998). Τρία χρόνια αργότερα, ο Τ. Hänsch, στο Ινστιτούτο Κβαντικής Οπτικής Max Planck (MPQ), στο Garching της Βαυαρίας, παρατήρησε για πρώτη φορά την μετάβαση Mott. Η επιστημονική εργασία στην οποία αναφέρθηκαν τα αποτελέσματα αυτού του πειράματος, είναι σήμερα μια από τις κορυφαίες στην ιστορία της φυσικής σε αριθμό βιβλιογραφικών αναφορών (Greiner et al, 2002).
Πώς όμως πραγματοποιείται αυτή η μεταβολή από μια υπερρευστή φάση σε έναν μονωτή; Η φυσική της βάση είναι το κβαντομηχανικό φαινόμενο σήραγγας. Χάρις σε αυτό το φαινόμενο είναι δυνατή η διάχυση των ατόμων σε διάφορες θέσεις μέσα στον οπτικό κρύσταλλο. Όπως γνωρίζουμε, στο συμπύκνωμα Bose-Einstein έχουμε το σχηματισμό ενός “γιγάντιου” υλικού κύματος που προκύπτει από την υπέρθεση ανάμεσα στα επιμέρους υλικά κύματα των ατόμων που συνιστούν το συμπύκνωμα μεταξύ των οποίων υπάρχει τέλεια συμφωνία φάσης. Όμως στα μακροσκοπικά κβαντικά πεδία[1] υπάρχει μια ενδογενής και θεμελιώδης απροσδιοριστία: κάθε φορά που η φάση είναι καθορισμένη ο αριθμός των ατόμων παρουσιάζει διακυμάνσεις και αντίστροφα. Αν, λοιπόν, καταφέρουμε να σταθεροποιήσουμε τον αριθμό των ατόμων σε όλες τις παγιδευτικές θέσεις, τότε η φάση θα γίνει εντελώς απροσδιόριστη και το “γιγάντιο” υλικό κύμα θα εξαφανιστεί. Ο αριθμός των ατόμων σε κάθε περιοχή παγίδευσης είναι συνεπώς ένας κρίσιμος παράγοντας. Ο μονωτής Mott είναι μια φάση του συστήματος όπου υπάρχει μόνο ένα άτομο σε κάθε τέτοια θέση. Τότε τα άτομα είναι απομονωμένα και κατά συνέπεια η μεταξύ τους αλληλεπίδραση είναι μηδενική[2]. Όλα τα παραπάνω είναι εφικτά γιατί το ενεργειακό βάθος των παγίδων σε έναν οπτικό κρύσταλλο μπορεί να γίνει αρκετά μεγάλο (απλά αυξάνοντας την ένταση του φωτός) οπότε η μετακίνηση των ατόμων ανάμεσα σε δύο γειτονικές θέσεις παγίδευσης είναι πρακτικά αδύνατη. Στα πειράματα στο MPQ κατόρθωσαν να μετατρέψουν ένα συμπύκνωμα Bose–Einstein σε μονωτή Mott και αντίστροφα πολλές φορές, αυξομειώνοντας το ενεργειακό βάθος των παγιδευτικών πηγαδιών.
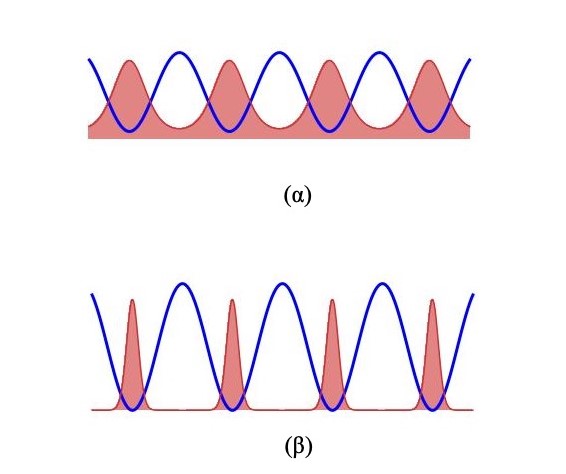
Εικόνα 1: (α) Ένα «ρηχό» πλέγμα οπτικού κρυστάλλου. Η πολυσωματιδιακή κατάσταση που δημιουργείται είναι ένα σύμφωνο υλικό κύμα μακροσκοπικής κλίμακας απεντοπισμένο σε όλο το χώρο του πλέγματος: κατάσταση υπερρευστότητας. (β) Ένα «βαθύ» οπτικό πλέγμα στο οποίο κάθε άτομο είναι εντοπισμένο σε μια δεδομένη περιοχή: κατάσταση μονωτή-Mott. Μπορούμε να μεταβαίνουμε από τη μια κατάσταση στην άλλη απλά μεταβάλλοντας το ενεργειακό βάθος του οπτικού πλέγματος. Καθώς το βάθος ελλατώνεται το άτομο, αξιοποιώντας το φαινόμενο σήραγγας, μπορεί να μεταπηδά από μια περιοχή σε άλλη και να μεταβαίνει από τη φάση του μονωτή σε αυτήν του υπερρευστού. Και στις δυό εικόνες οι συνεχείς γραμμές αναπαριστούν τα δυναμικά παγίδευσης των ατόμων και οι σκιασμένες περιοχές την πυκνότητα πιθανότητας που αντιστοιχεί στην κυματοσυνάρτηση των ατόμων.
Ένα σημαντικό χαρακτηριστικό αυτής της μεταβολής φάσης είναι πως μπορεί να επιτευχθεί ακόμη και σε θερμοκρασία ίση με το απόλυτο μηδέν. Σε ένα κλασικό σύστημα κάτι τέτοιο είναι αδύνατον γιατί οι απαραίτητες θερμικές διακυμάνσεις που προκαλούν αυτή τη μετάβαση δεν υπάρχουν. Σε ένα κβαντικό σύστημα, όμως, οι ενδογενείς διακυμάνσεις του κβαντικού κενού είναι ικανές να προκαλέσουν μια τέτοια μετάβαση. Αυτού του τύπου οι κβαντικές μεταβάσεις έχουν πολύ ενδιαφέρον για τη φυσική της συμπυκνωμένης ύλης και έχουν επίσης παρατηρηθεί σε υπεραγωγούς.
ΜΗ ΓΡΑΜΜΙΚΗ ΔΥΝΑΜΙΚΗ ΣΕ ΠΕΡΙΟΔΙΚΑ ΔΥΝΑΜΙΚΑ
Οι αντιδράσεις ανάμεσα στα άτομα, αν και ασθενείς, μπορεί να οδηγήσουν σε σημαντικά μη γραμμικά φαινόμενα στη φυσική συμπεριφορά των υλικών κυμάτων. Για παράδειγμα, στην κβαντική φυσική είναι γνωστό το φαινόμενο Josephson, που αφορά στην εμφάνιση ενός ηλεκτρικού ρεύματος ικανού να ρέει απεριόριστα, χωρίς την εφαρμογή κάποιας εξωτερικής τάσης, κατά μήκος μιας διάταξης γνωστής ως επαφής Josephson (Josephson, 1962). Η διάταξη αυτή αποτελείται από δύο υπεραγωγούς που διαχωρίζονται από ένα λεπτό μονωτικό υλικό. ‘Eνα συμπύκνωμα Bose-Einstein το οποίο βρίσκεται σε έναν ασθενή (αβαθή) οπτικό κρύσταλλο και στο οποίο οι αλληλεπιδράσεις μεταξύ των ατόμων είναι πολύ ισχυρές, μπορεί να περιγραφεί σαν μια διάταξη από επαφές Josephson (Anderson et al, 1998), (Cataliotti et al, 2001). Όταν το συμπύκνωμα παγιδευτεί σε δύο γειτονικές θέσεις ενός οπτικού κρυστάλλου, τα δύο επί μέρους συμπυκνώματα που προκύπτουν, αλληλεπιδρούν μέσω του φαινόμενου σήραγγας ανάμεσα στο φραγμό που χωρίζει τις δύο θέσεις. Ένα τέτοιο σύστημα είναι, στην πράξη, μια επαφή Josephson για ατομικά κβαντικά αέρια (Sukhatme et al, 2001). H μικρή απόσταση μεταξύ των δύο θέσεων του πλέγματος οδηγεί σε πολύ ισχυρό φαινόμενο σήραγγας ανάμεσα στα δύο συμπυκνώματα, γεγονός που εξασφαλίζει για το πείραμα μια επαρκή χρονική διάρκεια ώστε να μπορούν να εντοπιστούν και να μετρηθούν τα φαινόμενα της μη γραμμικής δυναμικής.
ΠΡΟΟΠΤΙΚΕΣ
Οι οπτικοί κρύσταλλοι ψυχρών ατόμων έχουν ανοίξει την πόρτα σε ένα ευρύ διαθεματικό πεδίο από τη μη γραμμική δυναμική έως τις ισχυρά συσχετισμένες κβαντικές φάσεις. Ένα από τα μεγάλα στοιχήματα αυτήν την εποχή είναι η διερεύνηση του φαινόμενου της υπεραγωγιμότητας, το οποίο βασίζεται στα λεγόμενα ζεύγη Cooper. Πρόκειται για ηλεκτρόνια, τα οποία, αν και φερμιόνια, σχηματίζουν ζεύγη που έχουν ακέραιο σπιν και, συνεπώς, συμπεριφέρονται ως μποζόνια. Οι οπτικοί κρύσταλλοι μπορεί να χρησιμοποιηθούν για τη δημιουργία καταστάσεων ζευγών Cooper από φερμιονικά άτομα. Σε αυτήν την περίπτωση θα μπορούμε να επιτύχουμε μια πολύ επιτυχημένη προσομοιώση του φαινόμενου της υπεραγωγιμότητας.
Άλλες ερευνητικές προσπάθειες εστιάζονται στην επίτευξη άμορφων συστημάτων. Πρόκειται για ισχυρώς αλληλεπιδρώντα κβαντικά συστήματα μέσα σε τυχαία δυναμικά που η θεωρητική τους ανάλυση είναι πολύ δύσκολη (Roth et al, 2003). Αξιοσημείωτη είναι η πρόβλεψη για την ύπαρξη μιας «υαλώδους» φάσης, σε ένα συμπύκνωμα Bose-Einstein, όταν αυτό παγιδευτεί σε ένα μονοδιάστατο οπτικό κρύσταλλο και αλληλεπιδράσει με τυχαία δυναμικά. Η κατάσταση του συμπυκνώματος είναι μονωτική και γεωμετρικά άμορφη, όπως το γυαλί, και θα μπορούσε να παρατηρηθεί πειραματικά (Lye et al, 2005).
Τα οπτικά πλέγματα προσφέρουν ενα ιδανικό περιβάλλον για την μελέτη της φυσικής συμπεριφοράς των φερμιονίων. Τα φερμιόνια, σε αντίθεση με τα μποζόνια απαιτούν περαιτέρω μελέτη για να αποκαλύψουν τις “λανθάνουσες” κβαντικές τους φάσεις. Τα φερμιόνια σε έναν οπτικό κρύσταλλο τριών διαστάσεων περιγράφονται από την θεωρία Hubbard η οποία θεωρείται πως “κρατάει” το μυστικό για την εξήγηση της υπεραγωγιμότητας υψηλών θερμοκρασιών (Anderson, 1987), (Hofstetter et al, 2002). Αν και αυτό το σύστημα έχει διερευνηθεί θεωρητικά για δεκαετίες εντούτοις, ακόμη, δεν έχουμε καταλήξει σε τελεσίδικα αποτελέσματα και στην πλήρη διαύγαση όλων των ερωτημάτων. Τα φερμιόνια σε οπτικά πλέγματα είναι κατάλληλα για ακριβείς μετρήσεις της επιτάχυνσης της βαρύτητας με συμβολόμετρα ατόμων (Roati et al, 2004). Επίσης, σε μίγματα διαφορετικών μποζονίων και φερμιονίων έχει προβλεφθεί η ύπαρξη «εξοτικών» κβαντικών φάσεων που δεν έχουν παρατηρηθεί στη συμβατική φυσική συμπυκνωμένης ύλης (Sanpera et al, 2004). Η ανάπτυξη νέας γενιάς ατομικών ρολογιών πολύ υψηλής ακρίβειας είναι ένα ακόμη πεδίο εφαρμογής των οπτικών κρυστάλλων ατόμων (εδώ). Σε αυτό το θέμα θα αναφερθούμε σε επόμενο άρθρο μας.
Οι οπτικοί κρύσταλλοι ατόμων, όταν το ενεργειακό βάθος τους μεταβάλλεται με το χρόνο, μπορούν να αξιοποιηθούν στην εξερεύνηση συστημάτων που λειτουργούν ως κβαντικές μηχανές. Αυτές είναι μικροσκοπικές συσκευές που εκμεταλλεύονται τους νόμους της κβαντικής μηχανικής για να παράγουν μηχανικό έργο. Η πρώτη κβαντική μηχανή κατασκευάστηκε το 2009 από μια ερευνητική ομάδα στο University of California, Santa Barbara (O’Connell et al, 2010). Μια μικροσκοπική «σανίδα» από αλουμίνιο συζεύχθηκε με έναν υπεραγώγιμο δακτύλιο, ο οποίος είναι στην πραγματικότητα ένας ηλεκτρονικό σύστημα δύο καταστάσεων αφού διαθέτει δύο δυνατές ενεργειακές κβαντικές καταστάσεις. Χειριζόμενοι αυτό το σύστημα με τη βοήθεια μικροκυμάτων, οι ερευνητές κατάφεραν να το τροφοδοτήσουν ή να αφαιρέσουν από αυτό κβάντα ενέργειας, όπως θα μπορούσε κανείς να χρησιμοποιήσει ένα ΑΤΜ για κατάθεση ή ανάληψη χρημάτων από έναν τραπεζικό λογαριασμό.
Ορισμένες ερευνητικές ομάδες έχουν προσπαθήσει να κατασκευάσουν κβαντομηχανικά συστήματα αντίστοιχα των κλασικών χαοτικών συστημάτων που συναντάμε στις μοριακές μηχανές. Σε αυτήν την περίπτωση τα άτομα μπορούν να τεθούν σε κίνηση ανοίγοντας και κλείνοντας ένα περιοδικό και ασύμμετρο οπτικό δυναμικό που προσομοιώνει την κίνηση μηχανικών γραναζιών (Ringot et al, 2000).
Η ανίχνευση ασθενών ηλεκτρομαγνητικών πεδίων είναι ένας άλλος τομέας στον οποίο οι οπτικοί κρύσταλλοι αφήνουν πολλές υποσχέσεις καθώς μπορούν να αποτελέσουν τη βάση για την κατασκευή υπερ-ευαίσθητων κβαντικών ανιχνευτών πεδίων τα οποία δεν μπορούν να ανιχνευτούν από αντίστοιχες κλασικές διατάξεις. Ιδαίτερες υποσχέσεις αφήνουν τα παγιδευμένα ιόντα σε οπτικούς κρυστάλλους εξαιτίας του γεγονότος πως οι πειραματικοί μπορούν να έχουν εξαιρετικό βαθμό ελέγχου των ιδιοτήτων τους και των παραμέτρων που είναι σημαντικές στο πείραμα καθώς και στη δυνατότητα να δημιουργούνται οι «πολυπόθητες» σύμπλεκτες κβαντικές καταστάσεις (quantum entangled states) ανάμεσα σε παγιδευμένα ιόντα. Πρόσφατα, ερευνητές στο National Institute of Standards and Technology (NIST) των ΗΠΑ κατόρθωσαν να κατασκευάσουν ένα τέτοιο οπτικό κρύσταλλο-ανιχνευτή με παγιδευμένα ιόντα βυρηλλίου με ικανότητα ανίχνευσης έως 20 φορές μεγαλύτερη από τις μέχρι τώρα διαθέσιμες ατομικές διατάξεις (Gilmore et al, 2021).
Τα οπτικά πλέγματα αποτελούν ένα πεδίο μελέτης ιδιαίτερα περίπλοκων προβλημάτων στην κβαντική χημεία, όπως ο ακριβής υπολογισμός της ηλεκτρονικής δομής των μορίων. Η ακριβής επίλυση τέτοιων προβλημάτων είναι πολύ δύσκολο έργο για τους συμβατικούς υπολογιστές. Οι ερευνητές πρότειναν πρόσφατα να το αντιμετωπίσουν χρησιμοποιώντας προσομοίωση προβλημάτων κβαντικής χημείας με τη βοήθεια ατόμων παγιδευμένων σε οπτικά πλέγματα που έχουν αναπτυχθεί εντός μιας ηλεκτρομαγνητικής κοιλότητας (Argüello-Luengo et al, 2019). Στην πρότασή τους, τα ηλεκτρόνια προσομοιώνονται με φερμιονικά άτομα που μετακινούνται μέσα στο δυναμικό του οπτικού πλέγματος, η έλξη από τον πυρήνα προσομοιώνεται με τη βοήθεια πρόσθετων οπτικών δυναμικών, ενώ η απωστική δύναμη Coulomb μεταξύ των ηλεκτρονίων προσομοιώνεται με την επίδραση του ηλεκτρομαγνητικού πεδίου της κοιλότητας στα παγιδευμένα άτομα.
Ένα άλλο ερευνητικό πεδίο στο οποίο οι οπτικοί κρύσταλλοι ατόμων μπορούν να έχουν σημαντική συνεισφορά είναι οι προσομοιώσεις της μεταβολής της κβαντικής φάσης που εικάζεται πως συνέβη στα πρώτα στάδια του σύμπαντος. Οι αναγνώστες του ΙnS γνωρίζουν πως η φυσική των ψυχρών ατόμων και συγκεκριμένα τα κβαντικά αέρια ατόμων έχουν αξιοποιηθεί πολλαπλώς σε αυτή το ερευνητικό πεδίο (εδώ). Η πιο πρόσφατη προσπάθεια σε αυτή την κατεύθυνση έγινε από τον Bo Song και τους συνεργάτες του στο Πανεπιστήμιο του Cambridge οι οποίοι αξιοποίησαν παγιδευμένα άτομα σε οπτικά πλέγματα και παρατήρησαν για πρώτη φορά ασυνεχείς μεταβάσεις από καταστάσεις μονωτή Mott σε μια υπερρευστη κατάσταση υψηλότερης ενέργειας στην οποία τα άτομα μπορούν να μετακινηθούν ελεύθερα μεταξύ διαφορετικών τοποθεσιών μέσα στο πλέγμα (Song et al, 2022). Η εμφάνιση ασυνεχών μεταβάσεων φάσεως προβλέπεται στο αρχικό στάδιο δημιουργίας του Σύμπαντος. Στο εν λόγω πείραμα επιτεύχθηκαν με διαταραχή του οπτικού κρύσταλλου.
Τέλος σε συστήματα που η συλλογική τους συμπεριφορά ακολουθεί τους νόμους της σχετικότητας μπορεί να εμφανιστεί μια ιδιαίτερης μορφής ταλάντωση, γνωστή ως διέγερση Higgs, η οποία μας είναι γνωστή από τον θεμελιώδη ρόλο που παίζει στο Καθιερωμένο Πρότυπο των στοιχειωδών σωματιδίων (το διάσημο, πλέον, «σωμάτιο του Higgs»). Η ανίχνευση αυτής της διέγερσης είναι αρκετά δύσκολη, γιατί έχει πολύ μικρό χρόνο ζωής, ο οποίος είναι ακόμη μικρότερος σε επίπεδα συστήματα δύο διαστάσεων, με αποτέλεσμα να έχουν εγερθεί σημαντικές αμφιβολίες για το κατά πόσο, τελικά, είναι δυνατή η ύπαρξή της. Σε συστήματα παγιδευμένων ατόμων σε οπτικούς κρυστάλλους έχει προβλεφτεί η ύπαρξη αυτής της ταλάντωσης στο όριο που τα άτομα μεταπίπτουν από τη φάση της υπερρευστότητας σε αυτήν του μονωτή. Πρόσφατα, ερευνητικές ομάδες από το Ινστιτούτο Μαξ Πλανκ, το Χάρβαρντ και το Ινστιτούτο Τεχνολογίας της Καλιφόρνια (CalTech), εργαζόμενες από κοινού, κατόρθωσαν να εντοπίσουν αυτές τις περιβόητες διεγέρσεις σε άτομα ρουβιδίου, που είχαν παγιδευτεί σε οπτικά πλέγματα δύο διαστάσεων (Endres et al, 2012).
Κλείνοντας αυτό το άρθρο θα πρέπει να αναφέρουμε τις πολύ μεγάλες προοπτικές για την αξιοποίηση των οπτικών πλεγμάτων στην κατασκευή κβαντικών πυλών που αποτελούν τα βασικά στοιχεία για την κατασκευή ενός κβαντικού υπολογιστή. Σε αυτό το θέμα θα αναφερθούμε εκτενώς σε επόμενη μας δημοσίευση.
Οι αναγνώστες του InS έχουν την ευκαιρία στα δύο άρθρα αυτού του αφιερώματος να λάβουν, ελπίζουμε, μια αρκετά λεπτομερή εικόνα για τις ιδιότητες και τις εφαρμογές των οπτικών κρυστάλλων οι οποίοι, μαζί με τα κβαντικά αέρια αποτελούν τα κορυφαία ίσως επιτεύγματα της σύγχρονης ατομικής φυσικής και βασικούς πυλώνες της αναγέννησης του πεδίου αυτού που λαμβάνει χώρα τις τελευταίες δεκαετίες (Lembessis, 2020).
ΕΥΧΑΡΙΣΤΙΕΣ
Η κεντρική εικόνα του άρθρου είναι ευγενική προσφορά στο InS του I. Bloch, καθηγητή στο Πανεπιστήμιο Ludwig Maximilian (LMU) του Μονάχου και Διευθυντή Ερευνών στο Ινστιτούτο Max Planck για την Κβαντική Οπτική στο Garching της Γερμανίας.
ΣΗΜΕΙΩΣΕΙΣ
[1] Ένα άλλο παράδειγμα μακροσκοπικού κβαντικού συστήματος είναι το φως του λέιζερ. Και σε αυτήν την περίπτωση υπάρχει μια σχέση απροσδιοριστίας ανάμεσα στον αριθμό των φωτονίων της δέσμης λέιζερ και στη φάση αυτής της δέσμης.
[2] Στην περίπτωση του μονωτή Mott ο αριθμός των ατόμων σε κάθε θέση είναι καθορισμένος οπότε, όπως εξηγήσαμε παραπάνω, η φάση είναι πλήρως απροσδιόριστη με αποτέλεσμα να μην μπορεί κάποιος να παρατηρήσει φαινόμενα συμβολής μεταξύ υλικών κυμάτων.
ΒΙΒΛΙΟΓΡΑΦΙΑ
Anderson, P., W., 1987. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198. DOI: 10.1126/science.235.4793.1196
Anderson, B., P., and Kasevich, M., A., 1998. Macroscopic quantum interferencefrom atomic tunnel arrays. Science 282, 1686–1689. 10.1126/science.282.5394.1686
Argüello-Luengo, J., González-Tudela, A., Shi, T., Zoller, P., and Cirac, J., I., 2019. Analogue quantum chemistry simulation. Nature 574, 215–218. 10.1038/s41586-019-1614-4
Ben Dahan, M., Peik, E., Reichel, J., Castin, Y., and Salomon, C., 1996. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508–4511. https://doi.org/10.1103/PhysRevLett.76.4508
Cataliotti, F., S., Burger, S., Fort, C., Maddaloni, P., Minardi, F., Trombettoni, A., Smerzi, A. and Inguscio, M., 2001. Josephson junction arrays with Bose–Einstein condensates. Science 293(5531), 843–846. 10.1126/science.1062612
Cohen-Tannoudji C. and Guéry-Odelin D., 2011. ADVANCES IN ATOMIC PHYSICS: An overview. New Jersey, USA. World Scientific, p. 671.
Endres, M., Fukuhara, T., Pekker, D., Cheneau, M., Schauss, P., Gross, C., Demler, E., Kuhr, S., and Bloch, I., 2012. The ‘Higgs’ amplitude mode at the two-dimensional superfluid/Mott insulator transition. Nature 487, 454–458. 10.1038/nature11255
Fertig, C., D., O’Hara, K., M., Huckans, J., H., Rolston, S., L., Phillips, W., D., and Porto, J., V., 2005. Strongly inhibited transport of a degenerate 1D Bose gas in a lattice. Phys. Rev. Lett. 94, 120403. https://doi.org/10.1103/PhysRevLett.94.120403
Feynman, R., 1982. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488. https://s2.smu.edu/~mitch/class/5395/papers/feynman-quantum-1981.pdf
Geiger, A., Z., Fujiwava, K., M., Singh, K., Senaratne, R., Rajagopal, S., V., Lipatov, M., Shimasaki, T., Driben, R., Konotop, V., Meier, T., and Weld, D., M., 2018. Observation and uses of position-space Bloch oscillations in an ultracold gas. Phys. Rev. Lett. 120, 213201. 10.1103/PhysRevLett.120.213201
Gilmore, K., A., Affolter, M., Lewis-Swan, R., J., Barberena, D., Jordan, E., Rey, A., M., and Bolinger J., J., 2021. Quantum-enhanced sensing of displacements and electric fields with two-dimensional trapped-ion crystals. Science 373, 673-678. DOI: 10.1126/science.abi5226
Girardeau, M. 1960. Relationship between systems of impenetrable bosons and fermions in one dimension. J. Math. Phys. 1, 516–523. https://doi.org/10.1063/1.1703687
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T., W., and Bloch, I., 2002. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44. 10.1038/415039a
Hofstetter, W., Cirac, J., I., Zoller, P., Demler, E., and Lukin, M., D., 2002. High-temperature superfluidity of fermionic atoms in optical lattices. Phys. Rev. Lett. 89, 220407. https://doi.org/10.1103/PhysRevLett.89.220407
Jaksch, D., Bruder, C., Cirac, J., I., Gardiner, C., W., and Zoller, P., 1998. Cold bosonic atoms in optical lattices. Phys. Rev. Lett. 81, 3108–3111.https://doi.org/10.1103/PhysRevLett.81.3108
Josephson, B., D., 1962. Possible new effects in superconductive tunnelling. Phys. Lett. 1, 251–253. https://doi.org/10.1016/0031-9163(62)91369-0
Lembessis, V. E., 2020. Taming Atoms: The Renaissance of Atomic Physics. Bellingham, Washington USA: SPIE. https://spie.org/Publications/Book/2563827?SSO=1
Lye, J. E., Fallani, L., Modugno, M., Wiersma, D., S., Fort, C., and Inguscio, M., 2005. Bose–Einstein condensate in a random potential. Phys. Rev. Lett. 95, 070401. https://doi.org/10.1103/PhysRevLett.95.070401
O’Connell, A., D., Hofheinz, M., Ansmann, M., Bialczak, R., C., Lenander, M., Lucero, M., Neeley, M., Sank, D., Wang, H., Weides, M., Wenner, J., Martinis, J., M., and Cleland, A., N., 2010. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464(7289), 697–703. 10.1038/nature08967
Ringot, J., Szriftgiser, P., Garreau, J., C., and Delande, D., 2000. Experimental evidence of dynamical localization and delocalization in a quasiperiodic driven system. Phys. Rev. Lett. 85, 2741–2744. https://doi.org/10.1103/PhysRevLett.85.2741
Roati, G., de Mirandes, E., Ferlaino, F., Ott, H., Modugno, G., and Inguscio, M., Atom interferometry with trapped Fermi gases. Phys. Rev. Lett. 92, 230402. https://doi.org/10.1103/PhysRevLett.92.230402
Roth R., and Burnett, K., 2003. Ultracold bosonic atoms in two-colour superlattices. J. Opt. B 5, S50–S54. https://iopscience.iop.org/article/10.1088/1464-4266/5/2/358
Sanpera, A., Kantian, A., Sanchez-Palencia, L., Zakrzwewski, J., and Lewenstein, M., 2004. Atomic Fermi–Bose mixtures in inhomogeneous and random lattices: from Fermi glass to quantum spin glass and quantum percolation. Phys. Rev. Lett. 93, 040401. https://doi.org/10.1103/PhysRevLett.93.040401
Song, B., Dutta, S., Bhave, S., Yu, Jr.-C., Carter, E., Cooper., N., and Schneider, U., 2022. Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. Nature Physics, 259-264. https://doi.org/10.1038/s41567-021-01476-w
Sukhatme, K., Mukharsky, Y., Chui, T., and Pearson, D., 2001. Observation of the ideal Josephson effect in superfluid 4He. Nature 411, 280–283. https://doi.org/10.1038/35077024
Tonks, L., 1936. The complete equation of state of one, two and threedimensional gases of hard elastic spheres. Phys. Rev. 50, 955–963. https://doi.org/10.1103/PhysRev.50.955




