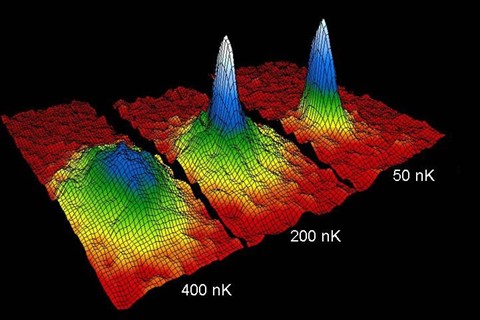
Απεικόνιση της κατανομής ταχυτήτων ενός δείγματος ατόμων. Αριστερά: σε θερμοκρασίες πάνω από την κρίσιμη, το ατομικό νέφος είναι σφαιρικό γεγονός που αποτελεί ένδειξη πως οι ταχύτητες των ατόμων κατανέμονται με βάση την κατανομή Boltzmann. Μέσον: κάτω από την κρίσιμη θερμοκρασία εμφανίζεται ένα μέγιστο σε ταχύτητα v=0, ένδειξη της συμπύκνωσης Bose-Einstein. Δεξιά: έπειτα από περαιτέρω ψύξη έχουμε ένα «καθαρό» συμπύκνωμα Bose-Einstein.( “Bose Einstein condensate” by NIST/JILA/CU-Boulder – NIST Image. Licensed under Public Domain via Wikimedia Commons)
Τα κβαντικά αέρια ατόμων αποτελούν εδώ και τρεις δεκαετίες μια πραγματικότητα που έχει αλλάξει ριζικά το τοπίο της ατομικής φυσικής και της φυσικής της συμπυκνωμένης ύλης. Η θεωρητική τους σύλληψη έγινε δυνατή πριν σχεδόν εκατό χρόνια. Τις τελευταίες δύο δεκαετίες τα κβαντικά αέρια άνοιξαν νέους ορίζοντες τόσο στη βασική φυσική όσο και σε μια σειρά εφαρμογές με κρίσιμο ρόλο στην ανάπτυξη των κβαντικών τεχνολογιών των επόμενων χρόνων. Σε αυτό το πρώτο μέρος παρουσιάζουμε μια σύντομη ιστορική ανασκόπηση των θεωρητικών και πειραματικών εργασιών πάνω στα κβαντικά αέρια καθώς και μια περίληψη των βασικών τους ιδιοτήτων.
Η ΘΕΩΡΗΤΙΚΗ ΣΥΛΛΗΨΗ
Τα κβαντικά αέρια είναι όχι μόνο άρρηκτα συνδεδεμένα με την κυματική φύση της ύλης, αλλά αποτελούν και μια από τις πιο θεαματικές επιβεβαιώσεις της. H περιπέτειά τους ξεκινά το 1924 όταν ο Ινδός φυσικός S. N. Bose, στο Πανεπιστήμιο της Dacca, πρότεινε μια εντελώς νέα απόδειξη του νόμου του Planck για την ακτινοβολία του μέλανος σώματος θεωρώντας τη θερμική ακτινοβολία ως ένα αέριο ταυτόσημων σωματιδίων (Bose, 1924). Στην απόδειξή του ο Bose βασίστηκε αποκλειστικά στη χρήση μεθόδων της στατιστικής φυσικής, αποφεύγοντας τις έννοιες και τα μεθοδολογικά/υπολογιστικά εργαλεία της ηλεκτροδυναμικής. Την ίδια χρονιά, ο Bose, έστειλε την εργασία με την πρότασή του για δημοσίευση αλλά, προς απογοήτευσή του, απορρίφθηκε. Αποφάσισε, τότε, να την ταχυδρομήσει στον Αϊνστάιν ζητώντας από αυτόν, εάν πίστευε πως είχε κάποια αξία, να μεσολαβήσει για τη δημοσίευσή της σε κάποιο γερμανικό περιοδικό. Πράγματι ο Αϊνστάιν, αφού πρώτα μελέτησε την εργασία προσεκτικά, την μετάφρασε στα γερμανικά και την προώθησε προς δημοσίευση χρησιμοποιώντας το αδιαμφισβήτητο κύρος του.
Ο Αϊνστάιν, σε δύο δημοσιεύσεις, το 1924 και το 1925, θα εφαρμόσει τις ιδέες του Bose στη μελέτη της κατάστασης ενός αερίου στο οποίο ο συνολικός αριθμός των μορίων (ή ατόμων) παραμένει σταθερός και θα αποδείξει πως σε εξαιρετικά χαμηλές θερμοκρασίες τα σωματίδια καταλαμβάνουν όλα μαζί την χαμηλότερη κβαντική ενεργειακή κατάσταση (Einstein 1924, 1925). Αυτή είναι η περίφημη συμπύκνωση Bose–Einstein, η οποία εμφανίζεται μόνο στα μποζόνια, δηλαδή σε σωμάτια στα οποία το σπιν είναι ακέραιο πολλαπλάσιο της ανηγμένης σταθεράς του Planck ħ (ħ = h/2π). Στη διεθνή βιβλιογραφία είναι γνωστή από το αγγλικό αρκτικόλεξο BEC (Bose-Einstein Condensation). Όπως έχει εύστοχα επισημανθεί, αυτή η θεαματική συνέπεια της κυματικής φύσης της ύλης διατυπώθηκε πριν ακόμη θεμελιωθούν οι γενικές αρχές της κβαντικής μηχανικής (Cohen-Tannoudji & Guéry-Odelin, 2011). Ο Bose δεν μπόρεσε να καταλήξει σε ένα τέτοιο συμπέρασμα επειδή μελέτησε την περίπτωση φωτονίων τα οποία, εφόσον έχουν μηδενική μάζα ηρεμίας, δεν χρειάζεται να οδηγηθούν σε συμπύκνωση καθώς όταν η ενέργεια του συστήματος ελαττώνεται αυτά εξαφανίζονται. Δύο χρόνια μετά τις δημοσιεύσεις του Αϊνστάιν ο E. Fermi και ο P. A. M. Dirac διαπίστωσαν πως η θεωρία των Βose-Einstein δεν μπορεί να εφαρμοστεί στην περίπτωση ηλεκτρονίων. Ο λόγος είναι πως το σπιν σωματιδίων όπως τα ηλεκτρόνια λαμβάνει τιμές που είναι ημιακέραια πολλαπλάσια της ανηγμένης σταθεράς του Planck (π.χ. ħ/2). Αυτά τα σωματίδια υπόκεινται στην Απαγορευτική Αρχή του Pauli και, όπως έχει αποδειχτεί, ακολουθούν μια διαφορετική στατιστική κατανομή γνωστή ως κατανομή Fermi–Dirac (Fermi, 1926), (Dirac, 1926) και γι’ αυτό το λόγο είναι γνωστά και ως φερμιόνια.
Για να εκδηλωθεί η συμπύκνωση Βose-Einstein θα πρέπει η θερμοκρασία των ατόμων να μειωθεί σε εξαιρετικά χαμηλά επίπεδα. Σε τέτοιες συνθήκες η μέση κινητική ενέργεια των ατόμων, άρα και η ορμή τους p, ελαττώνεται. Αυτό έχει ως συνέπεια το μήκος κύματος De Broglie (λdΒ =h/p) κάθε ατόμου να αυξάνει. Για να έχουμε μια εικόνα του προβλήματος αρκεί να αναφέρουμε πως σε ένα αέριο, σε συνήθη θερμοκρασία δωματίου, το μήκος κύματος de Broglie των ατόμων είναι περίπου δέκα χιλιάδες φορές μικρότερο από την μέση μεταξύ τους απόσταση. Σε μια τέτοια περίπτωση τα άτομα συμπεριφέρονται ως κλασικά σωμάτια και αλληλεπιδρούν μόνο κατά τη διάρκεια των μεταξύ τους κρούσεων. Καθώς η θερμοκρασία χαμηλώνει, τα άτομα αρχίζουν και συμπεριφέρονται σαν κύματα. Όταν η θερμοκρασία φτάσει σε μια κρίσιμη τιμή Tc, τα κύματα αυτά αρχίζουν να συμβάλουν και τα άτομα πλέον “χάνουν” την ταυτότητά τους. Σε αυτό το σημείο αναδύεται η κβαντική συμπεριφορά. Καθώς η θερμοκρασία συνεχίζει να ελαττώνεται τα άτομα μεταπίπτουν σε μια συλλογική κατάσταση, σαν πειθαρχημένα στρατιωτάκια, δημιουργώντας ένα “γιγάντιο” υλικό κύμα (Εικ. 1). Σε αυτήν την κατάσταση τα κύματα πιθανότητας που αντιστοιχούν σε κάθε σωμάτιο βρίσκονται σε απόλυτη συμφωνία φάσης.
Στην κλασική φυσική έχουμε πολλά παραδείγματα μεταβολών φάσης. Για παράδειγμα το λιώσιμο των πάγων ή η εξάτμιση ενός υγρού. Σε όλες αυτές τις περιπτώσεις παίζουν σημαντικό ρόλο οι αλληλεπιδράσεις μεταξύ των μορίων της ουσίας που υφίσταται την μεταβολή. Εδώ όμως τα πράγματα είναι αρκετά διαφορετικά. Ο ίδιος ο Αϊνστάιν περιέγραψε τη συμπύκνωση Βose-Einstein ως μια μεταβολή φάσης χωρίς τη μεσολάβηση κάποιας αλληλεπίδρασης. Πράγματι, κατά την εξέλιξη αυτού του φαινόμενου, το οποίο αποτελεί, πλέον, κλασικό παράδειγμα κβαντικής στατιστικής, τα άτομα μεταπίπτουν από μια κατάσταση που χαρακτηρίζεται από μια τεράστια ποικιλία ταχυτήτων σε μια κατάσταση με κοινή ταχύτητα. Αξίζει να σημειώσουμε πως η τιμή της κρίσιμης θερμοκρασίας, πέρα από την οποία αρχίζει η συμπύκνωση Βose-Einstein, είναι πολύ χαμηλή. Για παράδειγμα σε ένα αέριο από άτομα ρουβιδίου με πυκνότητα 1014 άτομα/cm3 η κρίσιμη θερμοκρασία είναι Tc = 350 nK. Σε αυτές τις θερμοκρασίες όλες οι ουσίες αναμένεται να βρίσκονται είτε στην υγρή είτε στην στερεά κατάσταση, οπότε η υπόθεση του Αϊνστάιν για ιδανικό αέριο δεν μπορεί να σταθεί. Αυτός ο λόγος σε συνδυασμό με το γεγονός πως δεν υπάρχει στην πράξη ένα ιδανικό αέριο ήταν η αιτία που όλοι οι επιστήμονες της εποχής, του Αϊνστάιν συμπεριλαμβανομένου, θεωρούσαν πως η προβλεπόμενη συμπύκνωση ήταν ένα καθαρά ακαδημαϊκό θέμα χωρίς πρακτική εφαρμογή.
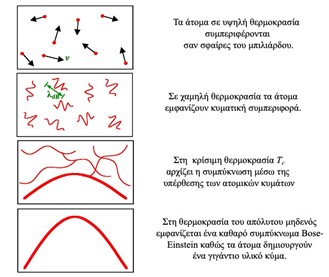
Εικόνα 1: Η φυσική συμπεριφορά των ατόμων καθώς ελαττώνεται η θερμοκρασία μέχρι την επίτευξη της συμπύκνωσης Bose-Einstein.
Η ΠΕΡΙΠΕΤΕΙΑ ΤΗΣ ΠΕΙΡΑΜΑΤΙΚΗΣ ΕΠΙΤΕΥΞΗΣ
Το πρώτο φυσικό σύστημα που σχετίστηκε με τη συμπύκνωση Βose-Einstein είναι το υγρό ήλιο 4He το οποίο παρουσιάζει μια «μυστηριώδη» συμπεριφορά σε πολύ χαμηλές θερμοκρασίες (κάτω των 2,17 Κ). Σε αυτή την περίπτωση το ήλιο μεταπίπτει από την υγρή φάση σε μια κατάσταση υπερρευστότητας όπου η ροή πραγματοποιείται χωρίς αντίσταση, σαν να μην ενεργούν εσωτερικές δυνάμεις τριβής στο υγρό. Τον Απρίλιο του 1938 ο F. London θα διατυπώσει την άποψη πως αυτή η μετάβαση θα μπορούσε να αποδοθεί, ή έστω να σχετίζεται, με την συμπύκνωση Βose-Einstein (London, 1938). Η παρατήρηση του London ενισχύθηκε από το γεγονός πως, σε αντίθεση με το 4He το οποίο είναι μποζόνιο, στο ισότοπο 3He, το οποίο παρουσιάζει φερμιονική συμπεριφορά (Σιμσερίδης, 2015) , δεν εμφανιζόταν το φαινόμενο της υπερρευστότητας.
Η πρώτη σημαντική θεωρητική ερμηνεία του φαινομένου της υπερρευστότητας δόθηκε από μια φαινομενολογική θεωρία που επινοήθηκε από τον L. D. Landau το 1941 και για την οποία, το 1962, τιμήθηκε με το Νόμπελ Φυσικής (Landau, 1941). Συνέχεια της εργασίας του Landau αποτέλεσε η ερευνητική εργασία του N. N. Bogoliubov το 1947 (Bogoliubov, 1947). Σε αυτήν την εργασία εισήγαγε τον μετασχηματισμό Bogoliubov, ο οποίος αργότερα αποδείχθηκε εξαιρετικά χρήσιμος στη μελέτη αρκετών φυσικών φαινομένων στην υπεραγωγιμότητα, στην πυρηνική φυσική και στα πιο πρόσφατα ατομικά συμπυκνώματα στα οποία θα αναφερθούμε στη συνέχεια. Στο ίδιο θέμα αξιόλογες ήταν και οι εργασίες που έγιναν από τον K. Huang και τους συνεργάτες του στη δεκαετία του 1950, οι οποίοι βασίστηκαν στη θεωρία των διαταραχών (Lee et al, 1957).
Το 1959 ο C. Hecht θα διατυπώσει την άποψη πως τα άτομα του υδρογόνου θα μπορούσαν να διατηρηθούν στην αέρια κατάσταση ακόμη και στη θερμοκρασία του απολύτου μηδενός στην περίπτωση που τα ηλεκτρόνιά τους έχουν καθορισμένο σπιν (Hecht, 1958). Το ενδιαφέρον σε αυτήν την περίπτωση είναι πως η κρίσιμη θερμοκρασία δεν είναι τόσο χαμηλή (συγκρινόμενη με αυτή για άτομα άλλων στοιχείων) εξαιτίας της μικρής μάζας του υδρογόνου. Η υπόδειξη του Hecht οδήγησε σε μια αναζωπύρωση της πειραματικής δραστηριότητας και η πρόβλεψή του επιβεβαιώθηκε πειραματικά το 1976 από τους W. Stwalley and L. Nosanow (Stwalley & Nosanow, 1976). Από τη στιγμή εκείνη αρχίζουν μια σειρά από πειράματα για την επίτευξη της συμπύκνωσης σε αέρια από άτομα υδρογόνου. Τα πειράματα αυτά αντιμετώπισαν αρκετές τεχνικές δυσκολίες. Στην προσπάθεια να ξεπεραστούν αυτά τα εμπόδια γεννήθηκαν μερικές από τις πιο σημαντικές ιδέες και τεχνικές που αργότερα θα ανοίξουν το δρόμο για τη συμπύκνωση Βose-Einstein σε αέρια από άλλα είδη ατόμων.
Λίγα χρόνια μετά θα αρχίσουν να εμφανίζονται τα θεαματικά επιτεύγματα πάνω στην επιβράδυνση και τον περιορισμό της ατομικής κίνησης σε αέρια ατόμων αλκαλίων (Lembessis, 2020). Οι τεχνικές αυτές άνοιξαν νέους δρόμους στην προσέγγιση πολύ χαμηλών θερμοκρασιών χωρίς την προσφυγή στις παραδοσιακές μεθόδους της κρυογενικής. Η βάση αυτών των επιτευγμάτων ήταν η αλληλεπίδραση του φωτός λέιζερ με τα άτομα για τα χαρακτηριστικά της οποίας έχουμε αναφερθεί σε προηγούμενο άρθρο μας στο InS. Με αυτές τις τεχνικές έγινε δυνατός ο περιορισμός των ατόμων σε μια περιοχή του χώρου χωρίς υλικά τοιχώματα που αποτελούσε πάντα έναν διακαή πόθο για τους πειραματικούς φυσικούς καθώς τα άτομα όταν προσεγγίζουν τα τοιχώματα ενός δοχείου μπορεί να προσκολληθούν σε αυτά και να εγκαταλείψουν την αέρια κατάσταση. Στη συγκεκριμένη περίπτωση οι ερευνητές ακολούθησαν μια μέθοδο παγίδευσης των ατόμων που στηρίζεται στη χρήση μαγνητικών πεδίων και είχε εισαχθεί από τον H. Hess τo 1986 για την παγίδευση ατόμων υδρογόνου (Hess 1986). Παρέμεναν όμως δύο ακόμη προβλήματα. Το πρώτο είχε να κάνει με το γεγονός πως η επιβράδυνση και η ταυτόχρονη παγίδευση των ατόμων μπορεί να οδηγήσει το δείγμα σε υψηλές πυκνότητες και κατά συνέπεια σε υγροποίηση και στερεοποίηση. Τα άτομα συνεπώς πρέπει να διατηρούνται διαρκώς στην αέρια φάση κάτι το οποίο μπορεί να εξασφαλιστεί μόνον όταν η πυκνότητα του δείγματος είναι αρκετά χαμηλή. Το δεύτερο είχε να κάνει με τη φυσική των τεχνικών επιβράδυνσης που βασίζεται στην ανταλλαγή φωτονίων μεταξύ της δέσμης λέιζερ και των ατόμων. Ακόμη και μια μεμονωμένη αυθόρμητη εκπομπή φωτονίου, λόγω διατήρησης της συνολικής ορμής, προσδίδει στο άτομο μια κινητική ενέργεια ίση με Ε = h2/(2Μλ), όπου Μ η μάζα του ατόμου και λ το μήκος κύματος του φωτονίου. Αυτό συνιστούσε ένα σοβαρό εμπόδιο στην προσπάθεια για την επίτευξη της επιθυμητής συμπύκνωσης καθώς αν και απειροελάχιστη σε μέγεθος (της τάξης των 10-29 Joule για ένα άτομο νατρίου) είναι ικανή να «θερμάνει» την ατομική κίνηση και να διαταράξει την όλη διαδικασία.
Η λύση σε αυτά τα προβλήματα ήλθε από την επιβράδυνση της ατομικής κίνησης μέσω εξάτμισης (evaporative cooling) που εφαρμόζεται σε άτομα που είναι ήδη παγιδευμένα (Masuhara et al, 1988). Η εξάτμιση, η οποία μας είναι ιδιαίτερα οικεία από τα σχολικά μας χρόνια, είναι ένας βασικός μηχανισμός ψύξης ενός υγρού όπου οι αλληλεπιδράσεις μεταξύ των μορίων διατηρούν τα μόρια στην υγρή φάση. Μέσω της εξάτμισης τα πιο γρήγορα μόρια μπορούν και υπερνικούν τη δυναμική ενέργεια αλληλεπίδρασης με τα υπόλοιπα μόρια και περνούν στην αέρια φάση, αφήνοντας πίσω στο υγρό τα πιο βραδυκίνητα μόρια. Αυτό οδηγεί στην ελάττωση της θερμοκρασίας και στην ψύξη του δείγματος. Μια ανάλογη εικόνα επαναλαμβάνεται στην περίπτωση των παγιδευμένων ατόμων. Όπως εξηγούμε στην Εικ. 2, μέσω των ελαστικών κρούσεων μεταξύ των ατόμων τα πιο ευκίνητα άτομα διαφεύγουν από την παγίδα αφήνοντας πίσω τα μόρια που έχουν χαμηλότερες ταχύτητες. Το τελικό αποτέλεσμα είναι πως η μέση κινητική ενέργεια του δείγματος ελαττώνεται και μαζί με αυτήν και η θερμοκρασία του.
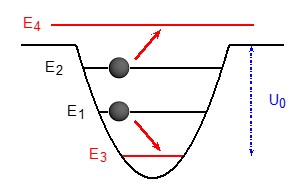
Εικόνα 2: Επιβράδυνση ατόμων μέσω εξάτμισης: Υποθέστε πως έχουμε δύο άτομα, με ενέργειες Ε1 και Ε2 αντίστοιχα, παγιδευμένα σε ένα δυναμικό με ενεργειακό βάθος U0. Σε κάποια στιγμή συμβαίνει μεταξύ τους μια ελαστική κρούση και τα άτομα αποκτούν ενέργειες Ε3 και Ε4 αντίστοιχα. Λόγω της ελαστικότητας της κρούσης η συνολική ενέργεια παραμένει σταθερή: Ε1+Ε2= Ε3+Ε4. Εάν Ε4> U0, τότε το άτομο με ενέργεια Ε4 διαφεύγει από την παγίδα και “εξατμίζεται”. Το άλλο άτομο, που παρέμεινε στην παγίδα, έχει πλέον μια ενέργεια Ε3 χαμηλότερη από την αρχική του Ε1. Με αυτόν το τρόπο το δείγμα των ατόμων που παραμένει στην παγίδα καταλήγει να είναι ψυχρότερο από το αρχικό.
Τα προβλήματα του συνδυασμού των διαφορετικών τεχνικών έλυσαν με τον βέλτιστο τρόπο οι ερευνητικές ομάδες των C. Wieman και E. Cornell στο Joint Institute for Laboratory Astrophysics (JILA) του Κολοράντο των ΗΠΑ και του W. Ketterle στο MIT το 1995 επιτυγχάνοντας τη συμπύκνωση Bose-Einstein χρησιμοποιώντας άτομα ρουβιδίου και νατρίου αντίστοιχα με διαφορά μόλις τεσσάρων μηνών (Anderson 1995), (Davis 1995). Για αυτές τις έρευνες οι εν λόγω επιστήμονες τιμήθηκαν με το βραβείο Νόμπελ φυσικής το 2001. Για να έχουμε μια πιο σαφή εικόνα της όλης διαδικασίας αξίζει να δούμε αναλυτικότερα τις λεπτομέρειες του πειράματος στο ΜΙΤ ώστε να καταλάβουμε το μέγεθος του επιτεύγματος. Οι ερευνητές χρησιμοποίησαν μια δέσμη από άτομα νατρίου που δημιουργήθηκε σε ένα φούρνο σε θερμοκρασία 600 Κ όπου η μέση ταχύτητα των ατόμων είναι γύρω στα 800 m/s. Η δέσμη των ατόμων είχε μια πυκνότητα της τάξης των 1014 ατόμων/cm3. Διανύοντας μια απόσταση μισού μέτρου τα άτομα επιβραδύνθηκαν, για πρώτη φορά, μέχρι η μέση ταχύτητά τους να φτάσει περίπου τα 30 m/s. Μετά την επιβράδυνση περίπου δέκα δισεκατομμύρια άτομα διοχετεύθηκαν σε μια Μαγνητο-Οπτική Παγίδα (Raab et al, 1987). Πρόκειται για μια διάταξη που συνδυάζει μαγνητικά πεδία και δέσμες λέιζερ για να επιτύχει ταυτόχρονα παγίδευση και επιβράδυνση της κίνησης των ατόμων. Με μια σειρά από περαιτέρω επιβραδύνσεις και παγιδεύσεις η κινητική θερμοκρασία του αερίου έπεσε στους 100 µK, που αντιστοιχεί σε μια μέση ταχύτητα 0,3 m/s. Η θερμοκρασία αυτή είναι υπεραρκετή ώστε τα άτομα να παγιδευτούν από μαγνητικά πεδία και να αρχίσει η ψύξη μέσω εξάτμισης η οποία υποβιβάζει την κινητική θερμοκρασία των ατόμων στους 2 µK (μέση ταχύτητα 0,4 mm/s) όπου αρχίζει η συμπύκνωση. Όλα αυτά σε χρόνο περίπου είκοσι δευτερολέπτων. Στο τελικό συμπύκνωμα παρέμειναν περίπου δέκα εκατομμύρια άτομα ενώ η διάμετρός του ήταν περίπου 0,3 χιλιοστά.
Θα πρέπει να σημειώσουμε πως η στροφή στην χρήση ατόμων από στοιχεία αλκαλίων δεν είναι διόλου τυχαία. Οι τεχνικές επιβράδυνσης και παγίδευσης με τη χρήση φωτός λέιζερ δεν μπορούσαν να εφαρμοστούν στο υδρογόνο. Επίσης, τα στοιχεία των αλκαλίων λόγω της ηλεκτρονικής τους δομής παρέχουν πληθώρα ισοτόπων με μποζονικό χαρακτήρα και μπορούν επίσης να διατηρηθούν στην αέρια κατάσταση για αρκετό χρόνο έτσι ώστε η συμπύκνωση να επιτευχθεί και να αναδυθεί ως μια μετασταθής κατάσταση πριν την υγροποίηση ή στερεοποίηση του δείγματος. Σημαντικό στοιχείο επίσης, από πειραματική άποψη, είναι η ύπαρξη πολύ αποτελεσματικών τεχνικών παρατήρησης του κβαντικού αερίου τόσο in situ όσο και εν κινήσει όταν αυτό αποτελείται από άτομα αλκαλίων. Αξίζει να σημειωθεί πως το 1998 θα επιτευχθεί τελικά και η συμπύκνωση του υδρογόνου με καθορισμένο σπιν από την ερευνητική ομάδα των T. Greytak και D. Kleppner στο MIT (Fried et al, 1998).
Η συμπύκνωση μας έδωσε τελικά ένα μακροσκοπικό κβαντικό αντικείμενο. Τα συμπυκνώματα Bose-Einstein αποτελούν, μαζί με το λέιζερ, τις δύο πιο σημαντικές μακροσκοπικές εκδηλώσεις της κβαντικής συμπεριφοράς. Θα πρέπει να σημειώσουμε πως το συμπύκνωμα που επιτεύχθηκε σε άτομα αλκαλίων απέχει αρκετά από την αρχική υπόθεση του Αϊνστάιν. Η πιο σημαντική διαφορά είναι πως ενώ πρόκειται για ένα μόρφωμα με πολύ χαμηλή πυκνότητα τα άτομα συνεχίζουν να αλληλεπιδρούν ισχυρά μεταξύ τους. Πράγματι η ενέργεια που αντιστοιχεί στην μεταξύ τους αλληλεπίδραση είναι ισχυρότερη κατά περίπου μιας τάξη μεγέθους σε σχέση με την δυναμική ενέργεια που έχουν εξαιτίας του δυναμικού της παγίδας μέσα στην οποία βρίσκονται. Αυτό δείχνει πως η τελική κατάσταση την οποία καταλαμβάνουν δεν είναι η θεμελιώδης ενεργειακή κατάσταση της παγίδας. Στο θεωρητικό μοντέλο του Αϊνστάιν τα άτομα δεν αλληλεπιδρούν μεταξύ τους οπότε μπορούν και καταλαμβάνουν αυστηρά την ίδια μονοσωματιδιακή κατάσταση που είναι η θεμελιώδης κατάσταση της παγίδας. Στην ουσία το φαινόμενο που παρατηρείται πειραματικά δεν είναι παρά μια κατανομή πληθυσμού όπως συμβαίνει και στην θερμική κατανομή των φωτονίων του μέλανος σώματος.
Οι αλληλεπιδράσεις μεταξύ των ατόμων διαδραματίζουν καθοριστικό ρόλο στον καθορισμό των ιδιοτήτων του συμπυκνώματος όπως το μέγεθός του και η ευστάθειά του. Οι διαφορές που παρατηρούνται, για παράδειγμα, σε συμπυκνώματα ατόμων διαφορετικών αλκαλίων οφείλονται τόσο στο διαφορετικό μέγεθος όσο και στον απωστικό ή ελκτικό χαρακτήρα των αλληλεπιδράσεων μεταξύ των ατόμων σε πολύ χαμηλές θερμοκρασίες. Ο συνδυασμός της παγίδευσης των ατόμων με τις μεταξύ τους αλληλεπιδράσεις τείνει να δημιουργεί συσχετίσεις μεγάλης κλίμακας ανάμεσα στα άτομα με τελικό αποτέλεσμα την εμφάνιση μιας συμφωνίας φάσης ανάμεσα σε αυτά παρόμοια με αυτήν που εμφανίζεται στα φωτόνια ενός λέιζερ. Τα συμπυκνώματα Βose-Einstein άνοιξαν το δρόμο για την κατασκευή του ατομικού λέιζερ (Mewes et al, 1997).
ΚΒΑΝΤΙΚΑ ΑΕΡΙΑ ΦΕΡΜΙΟΝΙΩΝ
Ένα ερώτημα που θα μπορούσε να προκύψει είναι κατά πόσο όλα τα παραπάνω επιτεύγματα μπορούν να επεκταθούν και σε φερμιόνια τα οποία έχουν μια ριζικά διαφορετική φυσική συμπεριφορά σε σχέση με τα μποζόνια. Τα φερμιόνια υπακούουν στην Απαγορευτική Αρχή του Pauli. Σύμφωνα με αυτήν την αρχή δεν είναι δυνατόν δύο όμοια φερμιόνια να καταλαμβάνουν την ίδια κβαντική κατάσταση ταυτόχρονα. Στα άτομα των φερμιονίων δεν εμφανίζεται κάποια «απότομη» μεταβολή φάσης όταν η θερμοκρασία ελαττώνεται. Αυτό συμβαίνει γιατί τα άτομα, στη θερμοκρασία του απόλυτου μηδενός, δεν μπορούν να εποικίσουν μια κοινή κατάσταση αλλά προοδευτικά καταλαμβάνουν ανώτερες ενεργειακά καταστάσεις με το πολύ ένα άτομο σε κάθε μια από αυτές (Εικ. 3). Η ανώτερη ενεργειακά κατειλημμένη κατάσταση ορίζει την λεγόμενη ενέργεια Fermi (περίπου 1μΚ ή 10-29 Joule για ένα αέριο φερμιονικών ατόμων). H Απαγορευτική Αρχή αποτελεί την αιτία της εμφάνισης της πίεσης Fermi. Όταν ένας μεγάλος αριθμός φερμιονίων περιοριστεί σε ορισμένο όγκο ασκεί πίεση όπως ακριβώς τα μόρια ενός αερίου ασκούν πίεση στα τοιχώματα ενός δοχείου. Η πίεση αυτή διαφέρει από την πίεση των αερίων που γνωρίζουμε από τα σχολικά μας χρόνια καθώς δεν απαιτείται συνεχής τροφοδοσία της ύλης με ενέργεια για να συντηρηθεί (Ξανθόπουλος, 1990). Εάν προσθέσουμε ένα παραπάνω φερμιόνιο σε ένα παγιδευμένο ιδανικό αέριο από Ν φερμιόνια, σε θερμοκρασία Τ = 0, αυτό θα τοποθετηθεί αναγκαστικά σε μια ενεργειακή στάθμη με ενέργεια μεγαλύτερη από την ενέργεια Fermi οδηγώντας σε αύξηση του μεγέθους του δείγματος. Οι χωρικές διαστάσεις ενός φερμιονικού αερίου συνεπώς σχετίζονται με την πίεση Fermi.
Η «ιδιόμορφη» κβαντική συμπεριφορά των φερμιονίων είναι η αιτία μιας σειράς φυσικών φαινομένων που ξεκινούν από την ποικιλία των ατόμων (οι δομικοί «λίθοι» των ατόμων, δηλαδή τα πρωτόνια, τα νετρόνια και τα ηλεκτρόνια είναι φερμιόνια) και φτάνουν μέχρι την ευστάθεια των λευκών νάνων και των αστέρων νετρονίων. Μια σημαντική ποιοτική διαφορά ανάμεσα στα φερμιονικά συστήματα που απαντώνται στη φύση και στα κβαντικά αέρια φερμιονικών ατόμων είναι πως τα δεύτερα χαρακτηρίζονται από χαμηλή πυκνότητα όπου οι αλληλεπιδράσεις μεταξύ των φερμιονίων είναι πολύ ασθενείς σε αντίθεση με τα πρώτα που δημιουργούνται σε συστήματα με πολύ υψηλές πυκνότητες φερμιονίων. Για παράδειγμα η πυκνότητα ενός αστέρα νετρονίων είναι της τάξης των 1017 kg/m3 ή περίπου 1038 νετρόνια/cm3.
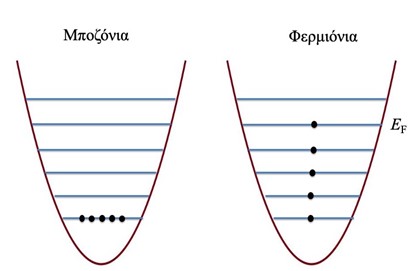
Εικόνα 3: Κβαντική στατιστική. Αριστερά: μποζόνια σε θερμοκρασία Τ=0. Όλα τα άτομα ενός ιδανικού συμπυκνώματος Bose-Einstein καταλαμβάνουν τη θεμελιώδη κατάσταση. Δεξιά: φερμιόνια ιδανικού αερίου. Όπως υπαγορεύει η Απαγορευτικής Αρχής του Pauli, κάθε ενεργειακό επίπεδο μπορεί να καταληφθεί από ένα, το πολύ, φερμιονικό άτομο. Σε θερμοκρασία Τ=0, η θεμελιώδης κατάσταση για ένα σύστημα από Ν φερμιόνια προκύπτει όταν καταληφθούν οι Ν χαμηλότερες ενεργειακά μονοσωματιδιακές καταστάσεις. H κατάσταση με την ανώτερη ενέργεια ορίζει την ονομαζόμενη ενέργεια Fermi ΕF.
Τα πρώτα πειράματα με άτομα του φερμιονικού δευτερίου (2H) ανάγονται στο 1980 (Silvera & Walraven, 1980) αλλά θα ξαναρχίσουν προς τα τέλη της δεκαετίας του 1990. Οι τεχνικές επιβράδυνσης και παγίδευσης φερμιονικών ατόμων είναι ίδιες με αυτές που εφαρμόζονται και σε αυτά με μποζονικό χαρακτήρα εκτός από την τελική επιβράδυνση μέσω εξάτμισης η οποία παρουσιάζει κάποιες διαφοροποιήσεις εξαιτίας της διαφορετικής φύσης των κρούσεων μεταξύ των ατόμων. Στα μποζονικά άτομα οι κρούσεις είναι ελαστικές «μετωπικές» (κρούση κύματος-s) στις οποίες δεν υπάρχει σχετική στροφορμή μεταξύ των ατόμων. Εξαιτίας της Απαγορευτικής Αρχής αυτές οι κρούσεις δεν μπορούν να συμβούν μεταξύ δύο φερμιονικών ατόμων που βρίσκονται στην ίδια εσωτερική κατάσταση (με ίδιο σπιν). Εντούτοις μπορούν να συμβούν εάν τα άτομα είναι σε διαφορετική εσωτερική κατάσταση. Το 1999 η ερευνητική ομάδα της D. Jinn στο JILA εκμεταλλευόμενη αυτό το γεγονός κατόρθωσε να δημιουργήσει το πρώτο αέριο φερμιονίων με άτομα καλίου (DeMarco, 1999). Στο πείραμα αυτό παρατήρησαν και ένα «παράξενο» φαινόμενο γνωστό ως αποκλεισμός Pauli (Pauli blocking) το οποίο παρουσιάζεται σε όλα τα φερμιονικά συστήματα. Εξαιτίας της Απαγορευτικής Αρχής ένα φερμιόνιο μπορεί να μεταβάλλει την ενέργειά του μόνο στην περίπτωση που η τελική κατάστασή στην οποία θα μεταβεί δεν είναι κατειλημμένη από κάποιο άλλο όμοιο φερμιόνιο. Σε ένα κβαντικό αέριο φερμιονίων οι χαμηλότερες καταστάσεις είναι σε μεγάλη πιθανότητα κατειλημμένες οπότε ο αποκλεισμός Pauli καταστέλλει κάθε διαδικασία στην οποία τα άτομα μεταβάλλουν την ενέργειά τους. Αυτό που είναι εξαιρετικά ενδιαφέρον σε αυτό το φαινόμενο είναι πως οι κρούσεις μεταξύ δύο ατόμων επηρεάζονται από την κατάσταση ατόμων που είναι πολύ μακριά μεταξύ τους. Το 2001 θα επαληθευτεί πειραματικά και η σχέση της μεταβολής του μεγέθους ενός αερίου Fermi με την πίεση Fermi (Trusscot et al, 2001).
ΕΠΙΛΟΓΟΣ
Τα κβαντικά αέρια αποτελούν κορυφαία επιτεύγματα της σύγχρονης ατομικής φυσικής. Σε επίπεδο βασικής επιστήμης αποτελούν πρότυπα συστήματα μελέτης της κβαντικής στατιστικής και της φυσικής της συμπυκνωμένης ύλης, ενώ σε επίπεδο εφαρμογών αναδεικνύονται σε έναν από τους βασικούς πυλώνες αυτού που αρκετοί ερευνητές αποκαλούν Δεύτερη Κβαντική Επανάσταση (Haroche & Raimond, 2006), εννοώντας την εμφάνιση και ραγδαία ανάπτυξη των νέων κβαντικών τεχνολογιών και τη μαζική τους χρήση στην βιομηχανία και την καθημερινότητα. Στο επόμενο σχετικό μας άρθρο θα αναφερθούμε στους νέους ορίζοντες που άνοιξαν στην επιστήμη της φυσικής καθώς και στις ποικίλες και συναρπαστικές εφαρμογές τους.
ΒΙΒΛΙΟΓΡΑΦΙΑ
Ξανθόπουλος, Β., 1990. Αστέρια: Η ζωή και ο θάνατός τους. Στο Ε. Ν. Οικονόμου, επιμ. Η ΦΥΣΙΚΗ ΣΗΜΕΡΑ ΙΙ. ΟΙ ΔΕΚΑ ΚΛΙΜΑΚΕΣ ΤΗΣ ΥΛΗΣ. Ηράκλειο: Πανεπιστημιακές Εκδόσεις Κρήτης, σ. 297. https://www.cup.gr/book/i-fisiki-simera-tomos-ii/
Σιμσερίδης, Κ., 2015. Καταστάσεις της Ύλης. Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών Βιβλιοθηκών, Εθνικό Μετσόβιο Πολυτεχνείο, σ. 36. https://repository.kallipos.gr/bitstream/11419/2117/3/Simseridis_Katastaseis_tis_ylis.pdf
Amico, A., Scazza, F., Valtolina, G., Tavares, P. E. S., Ketterle, W., Inguscio, M., Roati, G., and Zaccanti, M., 2018. Time-Resolved Observation of Competing Attractive and Repulsive Short-Range Correlations in Strongly Interacting Fermi Gases. Phys. Rev. Lett., 121, 253602. https://doi.org/10.1103/PhysRevLett.121.253602
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E., and Cornell, E. A., 1995. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science, 269, p. 198. DOI: 10.1126/science.269.5221.198
Bardeen, J., Cooper, L. N., and Schriefer, J. R., 1957. Microscopic Theory of Superconductivity. Physical Review, 106 (1), p. 162. https://doi.org/10.1103/PhysRev.106.162
Bardeen, J., Cooper, L. N., and Schriefer, J. R., 1957. Theory of Superconductivity. Physical Review, 108 (5), p. 1175. https://doi.org/10.1103/PhysRev.108.1175
Bogolyubov, N. N., 1947. A contribution to the theory of super-fluidity. (Russian) Bull. Acad. Sci. URSS. Sér. Phys. [Izvestia Akad. Nauk SSSR], 11, p. 77.
Bose, S. N., 1924. Plancks Gesetz und Lichtquantenhypothese (Planck’s Law and the Light Quantum Hypothesis). Z. Phys., 26, p. 178. http://dx.doi.org/10.1007/BF01327326
Cohen-Tannoudji C. and Guéry-Odelin D., 2011. ADVANCES IN ATOMIC PHYSICS: An overview. New Jersey, USA. World Scientific.
Davis, K. B., Mewes, M. -O., Andrews, M. R., van Druten, N. J., Durfee, D. S., Kurn, D. M., and Ketterle, W., 1995. Bose-Einstein condensation in a Gas of sodium Atoms. Phys. Rev. Lett., 75, p. 3969. https://doi.org/10.1103/PhysRevLett.75.3969
De Marco, B. and Jin, D. S., 1999. Onset of Fermi Degeneracy in a Trapped Atomic Gas. Science, 285, p. 1703. DOI: 10.1126/science.285.5434.1703
Dirac, P. A. M., 1926. On the Theory of Quantum Mechanics. Proc. Roy. Soc. A, 112, Issue 762, p. 661. https://doi.org/10.1098/rspa.1926.0133
Einstein, A., 1924. Quantentheorie des einatomigen idealen Gases (Quantum Theory of a Monoatomic Ideal Gas). Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, p. 261. https://doi.org/10.1002/3527608958.ch27
Einstein, A., 1925. On the Quantum Theory of a Monoatomic Ideal Gas. Sitzungsberichte der Preussischen Akademie der Wissenschaften, Berlin, Physikalisch-mathematische Klasse, 1, p. 18. https://einsteinpapers.press.princeton.edu/vol14-trans/448
Fermi, E., 1926. Sulla quantizzazione del gas perfetto monoatomico (On the quantization of an ideal monatomic gas). Rend. Lincei, 3, p. 145.https://sites.unimi.it/olivares/wp-content/uploads/2020/05/Fermi_gas_prefetto.pdf
Fried, D. G, Killian, T. C., Willmann, L., Landhuis, D., Moss, S. C., Kleppner, D., and Greytak, T. J., 1998. Phys. Rev. Lett., 81, p. 3811. https://doi.org/10.1103/PhysRevLett.81.3811
Haroche, S. and Raimond, 2006. Exploring the Quantum: Atoms, Cavities, and Photons, Oxford: Oxford University Press.https://oxford.universitypressscholarship.com/view/10.1093/acprof:oso/9780198509141.001.0001/acprof-9780198509141
Hecht, C. E., 1958. The possible superfluid behavior of hydrogen atom gases and liquids. Physica, 25, p. 1159. https://doi.org/10.1016/0031-8914(59)90035-7
Hess, H. F., 1986. Evaporative cooling of magnetically trapped atoms and compressed spin-polarized hydrogen. Phys. Rev. B, 34 (5), p. 3476. https://doi.org/10.1103/PhysRevB.34.3476
Jochim, S., Bartenstein, M., Altmeyer, A., Hendl, G., Riedl, S., Chin, C., Hecker-Denschlag, J., and Grimm, R., 2003. Bose-Einstein condensation of molecules. Science, 302, p. 2101. 10.1126/science.1093280
Ketterle, W. and Van Druten, N. J., 1996. Evaporative cooling of trapped atoms. Advances in atomic, molecular, and optical physics, 37, p. 181. https://doi.org/10.1016/S1049-250X(08)60101-9
Landau, L., 1941. Theory of the Superfluidity of Helium II. Phys. Rev., 60, p. 356.
https://doi.org/10.1103/PhysRev.60.356
Lee, T. D., Huang, K., and Yang, C. N., (1957). Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev., 106 (6), p. 1135. https://doi.org/10.1103/PhysRev.106.1135
Lembessis, V. E., 2020. Taming Atoms: The Renaissance of Atomic Physics. Bellingham, Washington USA: SPIE. https://spie.org/Publications/Book/2563827?SSO=1
Lett, P. D., Watts, R. N., Westbrook, C. I., Phillips, W. D., Gould, P. L., and Metcalf, H. J., 1988. Observation of Atoms Laser Cooled below the Doppler Limit. Phys. Rev. Lett., 61, p. 169. https://doi.org/10.1103/PhysRevLett.61.169
London, F., The λ-Phenomenon of Liquid Helium and the Bose-Einstein Degeneracy. Nature, 141, p. 643. https://doi.org/10.1038/141643a0
Masuhara, N., Doyle, J. M, Sandberg, J. C., Kleppner, D., Greytak, T. J., Hess, H. F., and Kochanski, G. P., 1988. Evaporative Cooling of Spin-Polarized Atomic Hydrogen, Phys. Rev. Lett., 61, p. 935. https://doi.org/10.1103/PhysRevLett.61.935
Mehboudi, M., Lampo, A., Charalambous, C., Correa L. A., García-March, M. Á., and Lewenstein, M., 2019. Using Polarons for sub-nK Quantum Nondemolition Thermometry in a Bose-Einstein Condensate. Phys. Rev. Lett., 122, 030403. https://doi.org/10.1103/PhysRevLett.122.030403
Mewes, M.-O., Andrews, M. P., Kurn, D. M., Durfee, D. S., Townsend, C. G., and Ketterle, W., (1997). Output coupler for Bose–Einstein condensed atoms. Physical Review Letters, 78, p. 582. https://doi.org/10.1103/PhysRevLett.78.582
Raab, E. L, Prentiss, M., Cable, A., Chu, S., and Pritchard, D. E., 1987. Trapping of Neutral Sodium Atoms with Radiation Pressure. Phys. Rev. Lett., 59, 2631. https://doi.org/10.1103/PhysRevLett.59.2631
Stwalley, W. C. and Nosanow, L. H., 1976. Possible “New” Quantum Systems. Phys. Rev. Lett., 36, p. 910. https://doi.org/10.1103/PhysRevLett.36.910
Silvera, I. F. and Walraven, J. T. M., 1980. Spin-Polarized Atomic Deuterium: Stabilization, Limitations on Density, and Adsorption Energy on Helium. Phys. Rev. Lett., 45, p. 1268. https://doi.org/10.1103/PhysRevLett.45.1268




