Στη μνήμη του Ευτύχη Μπιτσάκη
Βασίλης Λεμπέσης
Η κβαντική μηχανική είναι ίσως η πιο ενδιαφέρουσα και ταυτόχρονα αινιγματική θεωρία της σύγχρονης φυσικής καθώς οι νόμοι της φαίνονται συχνά παράδοξοι σε σχέση με την καθημερινή μας εμπειρία. Δύο από τις πιο γνωστές αλληγορίες που ενσαρκώνουν αυτή την κβαντική παραδοξότητα είναι η γάτα του Schrödinger και η γάτα του Cheshire. Η πρώτη σχετίζεται με την δυνατότητα ενός συστήματος να βρίσκεται σε δύο διαφορετικές καταστάσεις ταυτόχρονα. Η δεύτερη, που οφείλει το όνομά της σε έναν χαρακτήρα από το κλασικό βιβλίο “Η Αλίκη στη Χώρα των Θαυμάτων”, έχει γίνει σύμβολο ενός ακόμα πιο περίεργου κβαντικού φαινομένου: το διαχωρισμό ενός σωματιδίου από τις ιδιότητές του. Στο παρόν άρθρο, θα κάνουμε μια σύντομη αναφορά σε αυτές τις ιδέες και στους τρόπους με τους οποίους έχουν επιδειχθεί σε πειράματα, χρησιμοποιώντας παγιδευμένα ιόντα και φωτόνια σε οπτικές κοιλότητες. Το άρθρο ξεκινά με την παρουσίαση κάποιων βασικών αρχών που χρειάζονται στον αναγνώστη για να κατανοήσει το περιεχόμενο των θεμάτων που θα παρουσιάσουμε.
ΥΠΕΡΘΕΣΗ ΚΒΑΝΤΙΚΩΝ ΚΑΤΑΣΤΑΣΕΩΝ ΚΑΙ ΚΒΑΝΤΙΚΗ ΜΕΤΡΗΣΗ
Η κβαντική φυσική μίλησε εδώ και ένα αιώνα για την διπλή φύση της ύλης η οποία μας παρουσιάζεται πότε με το ένα πρόσωπό της ως σωματίδιο και πότε με το άλλο ως κύμα. Η παραδοχή αυτή άνοιξε τις πύλες ενός παράξενου κόσμου κυριαρχούμενου από φαινόμενα που ήταν εντελώς ανοίκεια στην αντίληψή μας. Ένα από αυτά ήταν η αρχή της υπέρθεσης των καταστάσεων (superposition principle) σύμφωνα με την οποία ένα σύστημα που έχει δύο ή περισσότερες δυνατές καταστάσεις (π.χ. ένας διακόπτης που μπορεί να είναι «ανοικτός» ή «κλειστός») συμπεριφέρεται εντελώς διαφορετικά στην κλασική και στην κβαντική του εκδοχή. Στη μεν κλασική εκδοχή μπορεί να βρίσκεται αποκλειστικά σε μια από τις δύο καταστάσεις, κάτι το οποίο πολύ εύκολα μπορούμε να το αποδεχτούμε. Ένας κβαντικός, όμως, διακόπτης μπορεί να βρίσκεται σε μια κατάσταση που αποτελεί ταυτόχρονα ένα συνδυασμό των δύο δυνατών καταστάσεων. Αν, για παράδειγμα, συμβολίσουμε την «ανοικτή» κατάσταση με |0⟩ και την «κλειστή» με |1⟩ τότε μια ισοπίθανη υπέρθεση αυτών των καταστάσεων συμβολίζεται από την κυματοσυνάρτηση[1] (wave function):
![Rendered by QuickLaTeX.com \[\( \Psi = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \).\]](https://inscience.gr/wp-content/ql-cache/quicklatex.com-987e461e854dba1719725bc009a88188_l3.png)
Η υπέρθεση των κβαντικών καταστάσεων, και κυρίως η διατήρησή της, προϋποθέτει μια «απομόνωση» του κβαντικού συστήματος. Αν προσπαθήσουμε να διαταράξουμε αυτήν την «απομόνωση», για παράδειγμα, εκτελώντας μια μέτρηση στο σωματίδιο, αυτό υπονοεί απαραίτητα μια αλληλεπίδραση με τη συσκευή μέτρησης. Ως αποτέλεσμα, το σωματίδιο καταρρέει σε μία από τις δύο πιθανές καταστάσεις του και παραμένει σε αυτήν. Αυτό οφείλεται στο ότι η μέτρηση, στην κβαντομηχανική, είναι μια μη αναστρέψιμη και εντελώς τυχαία διαδικασία. Ένα κβαντικό σύστημα έχει ένα σύνολο αποτελεσμάτων που προβλέπονται από την κατανομή πιθανότητας της κυματοσυνάρτησης. Τα αποτελέσματα είναι ντετερμινιστικά[2] αλλά όχι προβλέψιμα. Ακόμη πιο ενδιαφέρον είναι πως μετά από μια μέτρηση, ένα κβαντικό σύστημα παραμένει στην μετρούμενη κατάσταση καθώς σύμφωνα με το μετρητικό αξίωμα: οποιαδήποτε και αν είναι η κατάσταση ενός κβαντικού συστήματος πριν από μια μέτρηση ενός φυσικού μεγέθους, η κατάσταση μετά τη μέτρηση θα περιγραφεί από την ιδιοσυνάρτηση που αντιστοιχεί στην ιδιοτιμή του μεγέθους που μετρήθηκε (Τραχανάς, 2009). Στην κβαντομηχανική αυτό είναι γνωστό με τον όρο κατάρρευση της κυματοσυνάρτησης (collapse of wavefunction).
Η κατανόηση και η επεξήγηση της υπέρθεσης καταστάσεων είναι αρκετά δύσκολη, ακόμη και για καταξιωμένους φυσικούς, επειδή τα κβαντομηχανικά φαινόμενα έρχονται σε αντίθεση με την καθημερινή μας διαίσθηση. Ένα πολύ επιτυχημένο ανάλογο αυτής της έννοιας παρουσιάστηκε από τον C. R. Monroe και τον βραβευμένο με βραβείο Νόμπελ D. J. Wineland , και απεικονίζεται στην Εικ.1 (Monroe & Wineland, 2008). Στο παράδειγμά τους, οι Monroe και Wineland χρησιμοποιούν ένα φαινόμενο που μας είναι οικείο όταν προσπαθούμε να σχεδιάσουμε έναν κύβο σε ένα κομμάτι χαρτί. Το μάτι μας συνήθως «ξεγελιέται» και δεν μπορεί να ξεχωρίσει ποια πλευρά είναι στο προσκήνιο και ποια πίσω από αυτό. Αυτό είναι ένα ανάλογο της υπέρθεσης δύο κβαντικών καταστάσεων – ο κύβος είναι «αιωρούμενος» μεταξύ δύο διαφορετικών καταστάσεων. Όταν, όμως, προσπαθήσουμε να εστιάσουμε σε μία από τις δύο πλευρές, αυτή η πλευρά «μετακινείται» στο προσκήνιο, αφήνοντας την άλλη στο παρασκήνιο. Αυτό ισοδυναμεί με την εκτέλεση μιας μέτρησης σε ένα κβαντικό σύστημα.
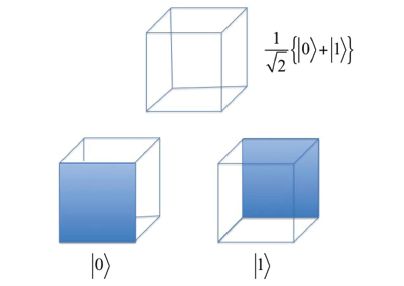
Εικ. 1. Όταν σχεδιάζουμε έναν κύβο σε ένα κομμάτι χαρτί, δημιουργείται μια ψευδαίσθηση η οποία μας εμποδίζει να διακρίνουμε αμέσως ποια πλευρά είναι η μπροστινή (|0⟩) και ποια η πίσω (|1⟩). Ο κύβος σε αυτή την περίπτωση (πάνω) βρίσκεται σε υπέρθεση δύο διαφορετικών καταστάσεων 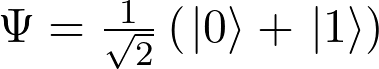 .(κάτω) Αν προσπαθήσουμε να εστιάσουμε σε μία από τις πλευρές, βλέπουμε |0> μπροστά ή |1> πίσω. Αυτό «ισοδυναμεί» με την εκτέλεση μιας κβαντομηχανικής μέτρησης (Lembessis, 2020).
.(κάτω) Αν προσπαθήσουμε να εστιάσουμε σε μία από τις πλευρές, βλέπουμε |0> μπροστά ή |1> πίσω. Αυτό «ισοδυναμεί» με την εκτέλεση μιας κβαντομηχανικής μέτρησης (Lembessis, 2020).
Η ΚΒΑΝΤΙΚΗ ΣΥΜΠΛΕΞΗ
Το άλλο κβαντικό φαινόμενο που φτάνει τη διαίσθηση και φαντασία μας στα όριά τους είναι η περίφημη κβαντική σύμπλεξη (quantum entanglement). Πρόκειται για ένα φυσικό φαινόμενο που εμφανίζεται όταν δημιουργούνται ή αλληλεπιδρούν μεταξύ τους κβαντικά σωματίδια ή σύνολα κβαντικών σωματιδίων με τέτοιο τρόπο ώστε η κβαντική κατάσταση κάθε σωματιδίου να μην μπορεί να περιγραφεί ανεξάρτητα από την κατάσταση των άλλων σωματιδίων, ακόμη και όταν τα δύο σωματίδια χωρίζονται από πολύ μεγάλες αποστάσεις. Η κατάσταση των σωματιδίων μπορεί να περιγραφεί μόνο ως κατάσταση ενός ενιαίου συστήματος. Αν, για παράδειγμα, έχουμε ένα σύστημα δύο σωματιδίων που μπορούν να βρίσκονται σε δύο δυνατές καταστάσεις, όπως στην προηγούμενη παράγραφο, τότε μια σύμπλεκτη κατάσταση περιγράφεται από την κυματοσυνάρτηση:
![Rendered by QuickLaTeX.com \[\( \Psi = \frac{1}{\sqrt{2}} (|0\rangle |0\rangle + |1\rangle |1\rangle) \).\]](https://inscience.gr/wp-content/ql-cache/quicklatex.com-77df6c0a625ff71919748213fcb22c1f_l3.png)
Ακολουθώντας ξανά τους Monroe και Wineland μπορούμε να πούμε πως η περίπτωση της κβαντικής σύμπλεξης είναι ανάλογη με το σχέδιο δύο πανομοιότυπων κύβων (Εικ. 2). Σε αυτή την περίπτωση, τα μάτια μας βλέπουν τους δύο κύβους άλλες φορές με τη μια πλευρά σε πρώτο πλάνο και άλλες φορές με την άλλη πλευρά σε πρώτο πλάνο. Οποιαδήποτε προσπάθεια εστίασης στο σχέδιο «αναγκάζει» τους κύβους να βρίσκονται στην ίδια κατάσταση, ανεξάρτητα από το αν υπάρχει κάποια «φυσική» σύνδεση μεταξύ τους.
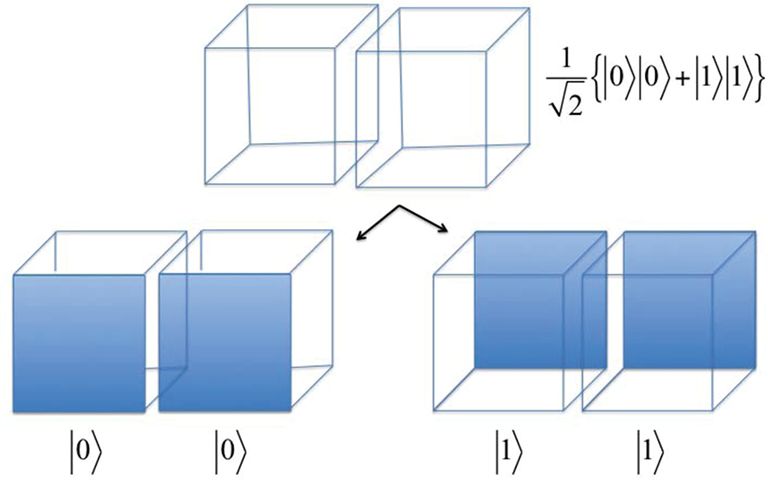
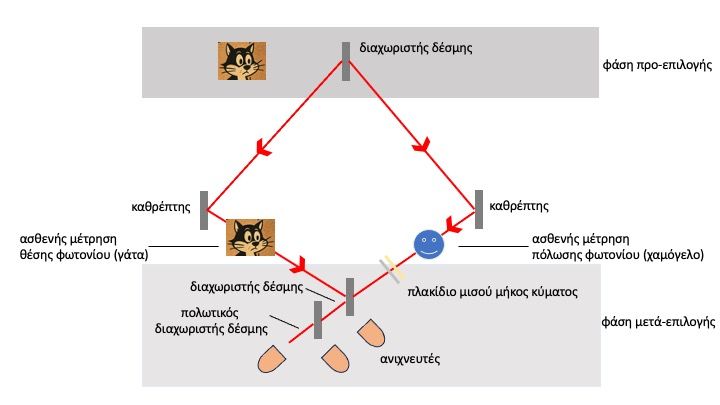
Εικ. 2. Σε αυτή την περίπτωση, βλέπουμε μια σύμπλεκτη κατάσταση που περιγράφεται από μια κυματοσυνάρτηση 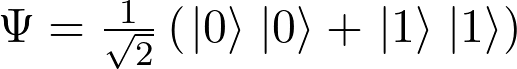 (πάνω). Μερικές φορές τα μάτια μας βλέπουν τους δύο κύβους με τη μία πλευρά μπροστά, και άλλες φορές με την άλλη πλευρά μπροστά. (κάτω μέρος). Οποιαδήποτε προσπάθεια εστίασης στο σχήμα κάνει τους κύβους να βρίσκονται στην ίδια κατάσταση, ανεξάρτητα από το αν υπάρχει φυσική σύνδεση μεταξύ τους. (Lembessis, 2021).
(πάνω). Μερικές φορές τα μάτια μας βλέπουν τους δύο κύβους με τη μία πλευρά μπροστά, και άλλες φορές με την άλλη πλευρά μπροστά. (κάτω μέρος). Οποιαδήποτε προσπάθεια εστίασης στο σχήμα κάνει τους κύβους να βρίσκονται στην ίδια κατάσταση, ανεξάρτητα από το αν υπάρχει φυσική σύνδεση μεταξύ τους. (Lembessis, 2021).
Η κβαντική σύμπλεξη χαρακτηρίστηκε το 1935 από τον E. Schrödinger ως η καρδιά και η ουσία της κβαντικής φυσικής—το φαινόμενο που διαχωρίζει ριζικά την κβαντική φυσική από την κλασική (Schrödinger, 1935). Η κβαντική σύμπλεξη σχετίζεται άμεσα με όλες τις περίφημες «ιδιοτροπίες» της κβαντικής φυσικής, όπως η αρχή του μη διαχωρίσιμου[3] (principle of inseparability) και η αρχή της συμπληρωματικότητας[4] (principle of complementarity) ενώ αποτελεί μαζί με την αρχή της υπέρθεσης τους πυλώνες του κβαντικού υπολογισμού και ως εκ τούτου της λειτουργίας των κβαντικών υπολογιστών.
Όπως έχει γραφτεί, η κβαντική σύμπλεξη μπορεί να θεωρηθεί ως ένας «αόρατος αγωγός» μεταξύ σωματιδίων που δεν έχει κλασικό ανάλογο (Monroe & Wineland, 2008). Είναι εξαιρετικά ενδιαφέρον, από την άποψη του Υπολογισμού, πως μια σύμπλεκτη κατάσταση μπορεί να περιέχει περισσότερες πληροφορίες από όσες είναι πιθανό να περιέχονται σε οποιαδήποτε κλασική κατάσταση με τον ίδιο αριθμό σωματιδίων. Το μείζον πρόβλημα με αυτές τις καταστάσεις είναι η ταχεία απώλεια της σύμπλεξης ως αποτέλεσμα κάθε λογής αλληλεπίδρασης με το περιβάλλον. Πολλοί πιστεύουν ότι αυτό και μόνο το γεγονός θέτει όρια στον κβαντικό υπολογισμό. Αυτό γιατί, με απλά λόγια, η συμφωνία είναι η αιτία που επιτρέπει σε ένα κβαντικό σύστημα να βρίσκεται ταυτόχρονα σε πολλαπλές καταστάσεις — κάτι σαν ένα τέλεια συγχρονισμένο πολυφωνικό τραγούδι. Όταν χάνεται αυτή η συμφωνία (quantum coherence) , το κβαντικό σύστημα «ξεχνά» τις εξαιρετικά λεπτές συσχετίσεις του και αρχίζει να συμπεριφέρεται σαν ένα κλασικό σύστημα, χάνοντας έτσι το κβαντικό του πλεονέκτημα. Χωρίς συμφωνία, οι κβαντικοί υπολογισμοί καταρρέουν — όπως μια μουσική συμφωνία που μετατρέπεται ξαφνικά σε θόρυβο. Για τον λόγο αυτό, η διατήρηση της συμφωνίας όσο το δυνατόν περισσότερο είναι θεμελιώδης προϋπόθεση για κάθε κβαντική τεχνολογία.
ΙΔΙΟΜΟΡΦΙΕΣ ΤΗΣ ΚΒΑΝΤΙΚΗΣ ΜΕΤΡΗΣΗΣ
Η εκτίμηση του φάσματος των δυνατών αποτελεσμάτων μιας μέτρησης ενός φυσικού μεγέθους σε ένα κβαντικό σύστημα και η εξαγωγή της αντίστοιχης κατανομής πιθανότητας προϋποθέτει την επανάληψη της μέτρησης στο σύστημα εκκινώντας κάθε φορά από τις ίδιες αρχικές συνθήκες. Όμως ανάμεσα στη θεωρία και την πράξη παρεμβάλλονται και οι εκάστοτε πειραματικές δυνατότητες που καθορίζονται σε μεγάλο βαθμό από το τεχνολογικό κεκτημένο κάθε εποχής.
Θα πρέπει να σημειώσουμε πως ήδη από τη δεκαετία του 1930 μεμονωμένα σωματίδια μπορούσαν να ανιχνευθούν και να μελετηθούν, για παράδειγμα σε θαλάμους με φυσαλίδες παρατηρώντας τα ίχνη τους ή τα υπολείμματά τους μετά τον θρυμματισμό τους εξαιτίας των μεταξύ τους ισχυρών συγκρούσεων. Σε αυτά τα πειράματα, η ύπαρξη των σωματιδίων και οι ιδιότητές τους συνήχθησαν, θα λέγαμε, «μεταθανάτια». Όπως έγραψε ο Schrödinger το 1952 αυτές οι μελέτες μοιάζουν με την εξονυχιστική ανάλυση αρχείων σχετικά με γεγονότα που έχουν συμβεί αρκετά πιο πριν (Schrödinger, 1952). Ο φυσικός σε αυτήν την περίπτωση μοιάζει με έναν αρχαιολόγο που προσπαθεί μέσα από ευρήματα να ανασκευάσει την ιστορία του παρελθόντος.
Οι πειραματικές προσπάθειες στις οποίες εμπλέκονται άτομα και φωτόνια δεν περιορίζονται μόνο στην ευαίσθητη ανίχνευση. Πρέπει να μπορούν όχι μόνο να ανιχνεύουν μεμονωμένα σωματίδια, αλλά να το κάνουν χωρίς να τα καταστρέφουν. Ο χειρισμός των σωματιδίων θα πρέπει να γίνεται με «χειρουργική» ακρίβεια ώστε να εξασφαλίζεται η επαναλαμβανόμενη παρατήρησή τους, σε αντίθεση με τις «στατικές» παρατηρήσεις που αναφέρθηκαν προηγουμένως. Η επανάληψη των μετρήσεων παρέχει πρόσβαση σε συσχετισμούς διαφόρων ειδών. Η κβαντική φυσική, στην ουσία της, περιγράφει και εξηγεί συσχετισμούς μεταξύ γεγονότων. Είναι επομένως απαραίτητο τα πειράματα που αφορούν στη διερεύνηση των αρχών της κβαντομηχανικής να μπορούν να εκτελούν επαναλαμβανόμενες μετρήσεις σε μεμονωμένα σωματίδια. Σε αυτή την περίπτωση, ο φυσικός δεν θα πρέπει να συγκρίνεται με τον παλαιοντολόγο, αλλά μάλλον με έναν βιολόγο που εργάζεται in vivo.
Η δραστική επίδραση μιας μέτρησης στη δυναμική ενός κβαντικού συστήματος ώθησε τους ερευνητές στην αναζήτηση τρόπων υπέρβασης αυτού του φαινομένου. Η μια λύση αναζητήθηκε στις λεγόμενες ασθενείς κβαντικές μετρήσεις (quantum weak measurements). Όπως δηλώνει και ο όρος πρόκειται για «απαλές» μετρήσεις οι οποίες δεν διαταράσσουν αρκετά την κατάσταση του κβαντικού συστήματος ούτως ώστε να αποφεύγεται η «ανεπιθύμητη» κατάρρευση της κυματοσυνάρτησης. Τα βασικά χαρακτηριστικά αυτής της πειραματικής μεθόδου είναι: η ελάχιστη διαταραχή στο σύστημα που εξασφαλίζει αποφυγή της κατάρρευσης της κυματοσυνάρτησης, ο περιορισμένος όγκος πληροφορίας που μπορεί να εξαχθεί σε μια μέτρηση επιβάλλοντας τον στατιστικό συνδυασμό πολλαπλών ασθενών μετρήσεων και, τέλος, η συχνή χρήση εκ των προτέρων (pre-selection) και εκ των υστέρων επιλογής (post selection) μιας κβαντικής κατάστασης για την αποκάλυψη πληροφοριών σχετικά με τα κβαντικά συστήματα μεταξύ των μετρήσεων. Κάτι που έχει ιδαίτερη σημασία είναι πως το αποτέλεσμα μιας μέτρησης μπορεί να βρίσκεται εκτός του φάσματος ιδιοτιμών («ασθενείς τιμές»). Θα πρέπει, επίσης, να τονιστεί πως ενώ η ιδέα της ασθενούς μέτρησης από μόνη της δεν φαίνεται να αποτελεί ριζική απόκλιση από τον κβαντικό φορμαλισμό, κατά την εκτέλεση των πειραμάτων ξεδιπλώθηκε ένας ολόκληρος νέος κόσμος από φαινόμενα που διέλαθαν της προσοχής των πειραματικών. Ανάμεσα σε αυτά και η τυχαία ανακάλυψη της γάτας του Cheshire που θα μας απασχολήσει στη συνέχεια.
Η άλλη μέθοδος είναι η λεγόμενη μη καταστροφική κβαντική μέτρηση (Quantum Non-Demolition Measurement) και είχε προταθεί από τον V. Braginsky και τους συνεργάτες του τη δεκαετία του 1970, στο πλαίσιο της ανίχνευσης βαρυτικών κυμάτων (Braginsky & Khalili, 1996). Βασικό χαρακτηριστικό αυτής της μεθόδου είναι η εκτέλεση μετρήσεων, μετά το πέρας των οποίων το κβαντικό σύστημα παραμένει άθικτο, επιτρέποντας την συνεχόμενη επανάληψη της μέτρησης σε αυτό. Τα βασικά της χαρακτηριστικά αυτής της πειραματικής μεθόδου είναι: α) Η ισχυρή αλλά προσεκτικά σχεδιασμένη μέτρηση ώστε να μην διαταράσσει το προς μέτρηση παρατηρήσιμο φυσικό μέγεθος, β) Το αποτέλεσμα της μέτρησης ανήκει στο φάσμα ιδιοτιμών, γ) Η διατήρηση του υπό παρατήρηση φυσικού μεγέθους ακόμη και σε διαδοχικές μετρήσεις. Η μη καταστροφική κβαντική μέτρηση χρησιμοποιείται συχνά για την παρακολούθηση συστημάτων με την πάροδο του χρόνου χωρίς να καταστρέφεται η κατάσταση τους (π.χ., στην κβαντική οπτική ή στην ανίχνευση βαρυτικών κυμάτων).
Η ΓΑΤΑ ΤΟΥ SCHRÖDINGER
Στην προσπάθειά τους να ερευνήσουν τα όρια και τις πιθανές αντιφάσεις των φυσικών θεωριών οι επιστήμονες κατέφυγαν από πολύ νωρίς στα περίφημα νοητικά πειράματα τα οποία στη διεθνή βιβλιογραφία είναι γνωστά με τον όρο gedankenexperiment. Πρόκειται για θεωρητικά σχήματα που, κατά κύριο λόγο, η σύλληψή τους γίνεται σε μια συγκεκριμένη ιστορική περίοδο, όταν οι πειραματικές και τεχνολογικές δυνατότητες ενός συγκεκριμένου τομέα έρευνας δεν είναι αρκετά ώριμες για την πραγματοποίησή τους. Αυτά τα πειράματα βοήθησαν, είτε στην ανάπτυξη επιστημονικών θεωριών, όπως οι θεωρίες της ειδικής και γενικής σχετικότητας, είτε στη διερεύνηση των ορίων εγκυρότητας μιας θεωρίας, όπως στην περίπτωση της κβαντικής μηχανικής.
Το 1935, ο Αυστριακός φυσικός Erwin Schrödinger πρότεινε ένα νοητικό πείραμα ως κριτική της ερμηνείας της Σχολής της Κοπεγχάγης για την κβαντομηχανική, ιδιαίτερα της ιδέας της κβαντικής υπέρθεσης και μέτρησης (Schrödinger, 1935). Στόχος του ήταν να δείξει αυτό που θεωρούσε παράδοξο ή παραλογισμό όταν οι κβαντικές αρχές εφαρμόζονται σε μακροσκοπικά αντικείμενα. Αν αποδεχτούμε την ερμηνεία της Κοπεγχάγης κυριολεκτικά, τότε θα καταλήξουμε στο ότι μια γάτα σε ένα κουτί θα μπορούσε να είναι ταυτόχρονα νεκρή και ζωντανή μέχρι κάποιος να ανοίξει το κουτί και να κοιτάξει – ένα σαφώς παράλογο συμπέρασμα. To νοητικό πείραμα του Schrödinger δίνει έμφαση στο πρόβλημα του πού και πώς συμβαίνει η κατάρρευση της κυματοσυνάρτησης. Είναι κατά τη διάρκεια της μέτρησης; Οφείλεται στην αλληλεπίδραση με το περιβάλλον; Ή μήπως συνδέεται με τη συνείδηση; Ο στόχος του Schrödinger δεν ήταν να υπονοήσει ότι οι γάτες βρίσκονται στην πραγματικότητα σε υπερθέσεις ζωής και θανάτου, αλλά να αναγκάσει τους φυσικούς και τους φιλοσόφους να αντιμετωπίσουν τις παράξενες επιπτώσεις της κβαντομηχανικής και να αμφισβητήσουν την πληρότητα ή τη συνέπεια της θεωρίας. Στην ουσία, ο Schrödinger χρησιμοποίησε τη γάτα για να αμφισβητήσει τα όρια μεταξύ κβαντικού και κλασικού κόσμου και να προκαλέσει συζήτηση σχετικά με την ερμηνεία της κβαντομηχανικής – μια συζήτηση που συνεχίζεται μέχρι σήμερα.
Φανταστείτε μια γάτα μέσα σε ένα κουτί, μαζί με μια μηχανή που μπορεί να σκοτώσει την γάτα με βάση την αποδιέγερση ενός ραδιενεργού ατόμου το οποίο μπορεί να εκπέμψει ένα φωτόνιο ή ένα ραδιενεργό σωματίδιο. Το άτομο αρχικά είναι διεγερμένο. Αν εκπέμψει, ο μηχανισμός ενεργοποιείται και σκοτώνει τη γάτα, αν όχι, τότε η γάτα παραμένει ζωντανή. Προϊόντος του χρόνου παραμονής στη διεγερμένη κατάσταση, το άτομο έχει εξελιχθεί σε μια υπέρθεση δύο καταστάσεων (αποδιέγερση ή μη), η μία από τις οποίες θα συνδεόταν με τη καταγραφή μιας νεκρής γάτας και η άλλη με την καταγραφή μιας ζωντανής γάτας. Σε αυτή την περίπτωση, το άτομο, ένα μικροσκοπικό σωματίδιο και η γάτα, ένα μακροσκοπικό σώμα, θα βρίσκονται σε μια σύμπλεκτη κατάσταση. Σύμφωνα με την καθιερωμένη ερμηνεία της κβαντικής μηχανικής, μέχρι να ανοίξουμε το κουτί, το άτομο βρίσκεται σε μια υπέρθεση καταστάσεων – δηλαδή, ταυτόχρονα έχει και δεν έχει αποδιεγερθεί. Και επειδή η ζωή της γάτας εξαρτάται από αυτό, η ίδια η γάτα βρίσκεται σε μια υπέρθεση ζωντανής και νεκρής κατάσταστασης ταυτόχρονα! Στην γλώσσα της κβαντικής μηχανικής η κατάσταση του συστήματος «μηχανισμός + γάτα» περιγράφεται από την παρακάτω σχέση:
![Rendered by QuickLaTeX.com \[|\Psi\rangle = \frac{1}{\sqrt{2}} \{|\zeta\omega\nu\tau\alpha\nu\eta\rangle|\mu\eta \ \alpha\pi\omicron\delta\iota\epsilon\gamma\epsilon\rho\sigma\eta\rangle + |\nu\epsilon\kappa\rho\eta\rangle|\alpha\pi\omicron\delta\iota\epsilon\gamma\epsilon\rho\sigma\eta\rangle\}\]](https://inscience.gr/wp-content/ql-cache/quicklatex.com-647a5e638c01993fa08c9868b7604a00_l3.png)
Πρόκειται για μια σύμπλεκτη κατάσταση όπου η κατάσταση της γάτας είναι συσχετισμένη με αυτήν του ατόμου.
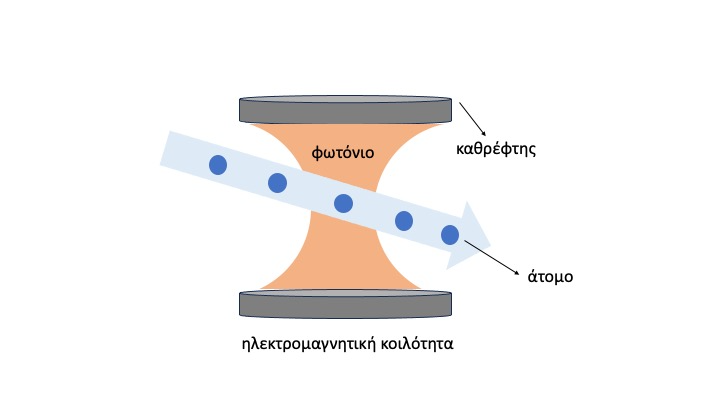
Το ερώτημα που τέθηκε ήταν αν κάτι τέτοιο μπορούσε να παρατηρηθεί στην πραγματικότητα. Η πειραματική υλοποίηση έγινε δυνατή τις τελευταίες δεκαετίες χάρις την αλματώδη ανάπτυξη νέων πειραματικών τεχνικών με ψυχρά άτομα και ιόντα καθώς και υψηλής ευαισθησίας φωτονικών κοιλοτήτων. Οι δύο διαφορετικές εκδοχές αυτών των πειραμάτων αποτελούν επί της ουσίας τις δύο πλευρές του ίδιου νομίσματος. Στην πρώτη περίπτωση στα πειράματα της École Normale Supérieure (ENS) στο Παρίσι, υπό την καθοδήγηση του Serge Haroche (βραβείο Νόμπελ 2012), χρησιμοποίησαν παγιδευμένα φωτόνια σε μια ηλεκτρομαγνητική κοιλότητα φτιαγμένη από καθρέφτες υψηλής ανακλαστικότητας και αξιοποίησαν δέσμες ατόμων για να ανιχνεύσουν και να χειριστούν αυτά τα φωτόνια και να μελετήσουν την εξέλιξή τους (Deleglise, 2008). Στην δεύτερη περίπτωση, υπό την καθοδήγηση του D. Wineland, στο National Institute of Standards and Technology (NIST) στο Boulder του Κολοράντο, έκαναν ακριβώς το αντίθετο: παγίδευσαν μεμονωμένα ιόντα, με τη βοήθεια ηλεκτρομαγνητικών πεδίων που παράγονται από ηλεκτρόδια και χρησιμοποιήσαν δέσμες λέιζερ για να χειριστούν και να ανιχνεύσουν τη συμπεριφορά αυτών των σωματιδίων.
I) ΟΙ ΓΑΤΕΣ ΤΗΣ ENS
Στα πειράματα της ENS βασικό ρόλο έπαιξε η χρήση ατόμων Rydberg, καθώς και η τεχνολογική πρόοδος στην κατασκευή ηλεκτρομαγνητικών κοιλοτήτων υψηλής πιστότητας. Μέχρι τις αρχές της δεκαετίας του 1970, στην έρευνα πάνω στα φάσματα των ατόμων υπήρχε μια terra incognita, όπως πολύ γλαφυρά έχει αναφέρει ο Haroche στην διάλεξη για την απονομή του βραβείου Νόμπελ (Haroche, 2013). Πρόκειται για μια περιοχή δέσμιων καταστάσεων των ηλεκτρονίων πολύ κοντά στο όριο ιονισμού. Οι καταστάσεις αυτές είναι γνωστές ως καταστάσεις Rydberg (Rydberg states). Το βασικό χαρακτηριστικό τους είναι η πολύ μεγάλη απόσταση των ηλεκτρονίων από τον πυρήνα[5], γεγονός που δίνει σε αυτές τις καταστάσεις πολύ μεγάλες διπολικές ροπές και καθιστά αυτά τα άτομα εξαιρετικά ευαίσθητα στις αλληλεπιδράσεις τους με την ακτινοβολία μικροκυμάτων. Μια άλλη σημαντική ιδιότητα αυτών των καταστάσεων είναι ο μεγάλος χρόνος (για την κλίμακα των κβαντικών φαινομένων) που επιβιώνει το ηλεκτρόνιο όταν διεγερθεί και μεταβεί σε μια τέτοια διεγερμένη κατάσταση, που μπορεί να φτάσει τα 30 ms, και είναι της ίδιας τάξης μεγέθους με το χρόνο ζωής των φωτονίων μέσα στην κοιλότητα.
Μια σειρά από πειραματικά επιτεύγματα στην αλληλεπίδραση των ατόμων Rydberg με εξελιγμένες «εκδόσεις» των ηλεκτρομαγνητικών κοιλοτήτων οδήγησαν αφενός, στην δημιουργία ενός ερευνητικού πεδίου γνωστού ως Κβαντική Ηλεκτροδυναμική Κοιλότητας[6](Cavity Quantum Electrodynamics, CQED) αφετέρου στη δημιουργία του βασικού εργαλείου με το οποίο θα αποκαλύπτονταν τα μυστικά των κβαντικών ιδιοτήτων των ηλεκτρομαγνητικών πεδίων[7]. Η εξέλιξη των πειραμάτων οδήγησε στην ανάπτυξη διατάξεων όπου τα άτομα Rydberg αλληλεπιδρούσαν πλέον με ηλεκτρομαγνητικά πεδία μέσα στην κοιλότητα, τα μήκη κύματος των οποίων ήταν πλέον στην περιοχή του ορατού ηλεκτρομαγνητικού φάσματος (Jhe et al, 1987)[8]. Το άλλο σημαντικό εμπόδιο που έπρεπε να υπερβληθεί ήταν η εκτέλεση μετρήσεων μετά το πέρας των οποίων το φωτόνιο θα έμενε άθικτο επιτρέποντας την συνεχή επανάληψη της μέτρησης στο ίδιο φωτόνιο. Οι ερευνητές στην ENS χρειάστηκε να προσαρμόσουν τις τεχνικές μη καταστροφικής μέτρησης στην ανίχνευση κβάντων φωτός για να μπορέσουν να το επιτύχουν.
Εικ. 3. Σχηματική αναπαράσταση της διάταξης που χρησιμοποιήθηκε στα πειράματα στην ENS για την παρατήρηση της Γάτας του Schrödinger
Σε αυτά τα πειράματα τον ρόλο της «δολοφονικής συσκευής» έπαιξε ένα μόνο άτομο σε μια υπέρθεση δύο εσωτερικών καταστάσεων Rydberg. To ρόλο της «γάτας» έπρεπε να παίζει ένα σύστημα το οποίο με κάποιο τρόπο θα μπορεί να αποκτήσει μια κλασική συμπεριφορά. Κάτι τέτοιο μπορούν να μας προσφέρουν οι λεγόμενες σύμφωνες καταστάσεις (coherent states). Πρόκειται για κβαντικές καταστάσεις στις οποίες ελαχιστοποιείται η τιμή της σχέσης αβεβαιότητας[9] και των οποίων οι μέσες τιμές ακολουθούν κλασικές εξισώσεις κίνησης[10].
Το άτομο μέσω της υπέρθεσης των καταστάσεων κατά την αλληλεπίδρασή του με το σύμφωνο πεδίο της κοιλότητας «ελέγχει» την φάση του πεδίου η οποία μπορεί να λαμβάνει δύο διαφορετικές τιμές ταυτόχρονα, τη μία εξ’ αυτών μπορούμε να ονομάσουμε «ζωντανή» και την άλλη «νεκρή». Ο προσεκτικός αναγνώστης θα μπορούσε να αναρωτηθεί πως είναι δυνατόν ένα και μόνο άτομο να επηρεάζει τη φάση ενός πεδίου που αποτελείται από πλήθος φωτονίων. Η απάντηση βρίσκεται αποκλειστικά στην πανίσχυρη αλληλεπίδραση ενός ατόμου Rydberg με το πεδίο. Το άτομο μετατρέπεται σε ένα μέσο με πολύ μεγάλο δείκτη διάθλασης ικανό να επηρεάζει μακροσκοπικά την κατάσταση ενός πεδίου.
II) ΟΙ ΓΑΤΕΣ ΤOΥ NIST
Η επόμενη οικογένεια πειραμάτων στα οποία υλοποιήθηκε η ιδέα της Γάτας του Schrödinger έλαβε χώρα στο εργαστήριο του NIST υπό την επίβλεψη του David Wineland. Για να φτάσουν στο επίτευγμα αυτό έπρεπε να προηγηθούν μια σειρά πειράματα. Τα πρώτα από αυτά αφορούσαν στην απομόνωση μεμονωμένων ιόντων η οποία μπορεί να γίνει εφικτή μέσω της αλληλεπίδρασής τους με κατάλληλα ηλεκτρομαγνητικά πεδία. Αξιοσημείωτα ήταν τα πειράματα με ιόντα Ba+ στα οποία, εκτός των άλλων, με τη βοήθεια ενός μεγεθυντικού φακού, περισυνελλέγει και κατέστη ορατό από το ανθρώπινο μάτι το φως από τον φθορισμό ενός και μόνο ιόντος (Neuhauser et al. 1980). Στα πειράματα στο NIST επικεντρώθηκαν αρχικά σε ιόντα Hg+ εξαιτίας μιας σειράς πειραματικών πλεονεκτημάτων στην χρήση τους . Στην καταγραφή του φθορισμού των ιόντων έγινε χρήση τεχνικών μη καταστροφικής κβαντικής μέτρησης[11].
Το επόμενο βήμα ήταν ο έλεγχος της εξωτερικής (μεταφορικής) κίνησης των ιόντων και ακόμη περισσότερο η συσχέτιση της με την εσωτερική κατάσταση του ιόντος. Η μεταφορική κίνηση επιβραδύνθηκε σε πολύ μεγάλο βαθμό με τη χρήση φωτός λέιζερ και σε συνδυασμό με την επίδραση των πεδίων της παγίδας μετατράπηκε, επί της ουσίας, σε μια απλή αρμονική κίνηση γύρω από μια θέση ισορροπίας. Με απλά λόγια η κίνηση του ιόντος ήταν παρόμοια με αυτήν ενός σωματιδίου προσκολλημένου σε ένα ελατήριο. Ο λόγος που οι επιστήμονες επιδίωξαν τον ακριβή έλεγχο της ιοντικής κίνησης ήταν για να μπορέσουν αρχικά να τοποθετήσουν το ιόν στην θεμελιώδη ενεργειακή κατάσταση της παγίδας. Αυτό ήταν προαπαιτούμενο ώστε να είναι σε θέση να κατασκευάσουν πιο σύνθετες καταστάσεις της μεταφορικής κίνησης του ιόντος με τελικό στόχο να επιτύχουν την κατασκευή μιας σύμφωνης κατάστασης.
Η βασική φυσική διαφορά ανάμεσα στα πειράματα στην ENS και σε αυτά στο NIST είναι ο χαρακτήρας και ο ρόλος του «αρμονικού ταλαντωτή» που χρειαζόμαστε ώστε να κατασκευάσουμε σύμφωνες καταστάσεις. Στη μεν πρώτη περίπτωση αυτόν τον ρόλο τον είχε το ηλεκτρομαγνητικό πεδίο της κοιλότητας ενώ στη δεύτερη περίπτωση η παγιδευμένη μεταφορική κίνηση του ιόντος. Με την πάροδο των ετών, αυτή η αντιστοιχία έχει οδηγήσει σε μερικά ενδιαφέροντα και συμπληρωματικά πειράματα μεταξύ των δύο τύπων πειραμάτων (Haroche & Raimond, 2006).
Για να φτάσουν στην υλοποίηση του στόχου τους στο NIST χρειάζονταν έναν μηχανισμό που θα έπαιζε το ρόλο της «δολοφονικής διάταξης» (του ραδιενεργού σωματιδίου στο νοητικό πείραμα του Schrödinger). Στη συγκεκριμένη περίπτωση χρειάζονταν κάτι που να συμπλέκει την μεταφορική κίνηση του ιόντος με την εσωτερική του κατάσταση (Wineland, 2013). Aυτό μπορεί να συμβεί όταν το ιόν αλληλεπιδράσει με το φως του λέιζερ το οποίο έχει σχεδόν αυστηρά καθορισμένη συχνότητα και πόλωση. Με αυτόν τον τρόπο επάγει μεταβάσεις ενός ηλεκτρονίου μεταξύ δύο μόνο συγκεκριμένων ενεργειακών σταθμών του ιόντος η χαμηλότερη (ενεργειακά) εκ των οποίων ονομάζεται θεμελιώδης και η ανώτερη διεγερμένη. Με την κατάλληλη εφαρμογή ενός παλμού λέιζερ ασκήθηκε στο ιόν, μια δύναμη, γνωστή ως οπτική διπολική δύναμη (optical dipole force), η οποία εξαρτάται από την εσωτερική κατάσταση του ιόντος (Monroe et al. 1996). Σαν αποτέλεσμα, όταν το ηλεκτρόνιο είναι στην διεγερμένη κατάσταση (αποδιέγερση στο νοητικό πείραμα) το ιόν κινείται προς μια συγκεκριμένη κατεύθυνση (νεκρή γάτα) ενώ αν το ηλεκτρόνιο βρεθεί στην θεμελιώδη κατάσταση (μη αποδιέγερση) το ιόν θα κινηθεί προς αντίθετη κατεύθυνση (ζωντανή γάτα).
Εικ. 4. Σχηματική αναπαράσταση της διάταξης που χρησιμοποιήθηκε στα πειράματα στο NIST για την παρατήρηση στους Γάτας του Schrödinger.
H πιο βασική ένσταση που υπάρχει σε αυτά τα πειράματα που προαναφέραμε έχει να κάνει με το «μέγεθος» στους «γάτας». Στο νοητικό πείραμα του Schrödinger η γάτα επιλέχτηκε γιατί αντιπροσωπεύει ένα «μακροσκοπικό αντικείμενο» η συμπεριφορά του οποίου καθορίζεται από την κλασική φυσική. Σε αυτά τα πειράματα τίθεται αμέσως το ερώτημα: πως μπορούν φωτόνια και ιόντα να αποκτήσουν μια «μακροσκοπική δυναμική» ώστε να προσομοιώνουν τη συμπεριφορά ενός κλασικού αντικειμένου; Η απάντηση βρίσκεται στους σύμφωνες καταστάσεις που δεν έχουν επιλεγεί τυχαία καθώς είναι οι κβαντικές καταστάσεις που, όπως προαναφέραμε, προσεγγίζουν πιο πολύ μια κλασική κατάσταση. Αυτό επιτρέπει στα μεν πειράματα του Haroche τον εποικισμό αυτών των καταστάσεων με περισσότερα φωτόνια, στα δε πειράματα του Wineland την εκτέλεση ταλαντώσεων με όλο και μεγαλύτερο πλάτος στους δύο διαφορετικές κατευθύνσεις[12]. Το μεγάλο τίμημα σε αυτές τις περιπτώσεις είναι πως τα συστήματα γίνονται ευάλωτα ακόμη και σε ασθενέστατες αλληλεπιδράσεις με το περιβάλλον (διακυμάνσεις στην ένταση και την φάση των λέιζερ, μηχανικές ταλαντώσεις κλπ.) με αποτέλεσμα την απώλεια της πολύτιμης συμφωνίας (Myatt et al., 2000a,b; Turchette et al., 2000). Ωστόσο, οι επιστήμονες θεωρούν πως αυτό το πρόβλημα είναι απλά τεχνικής φύσεως και όχι ένας βαθύτερος θεμελιώδης περιορισμός, και πως τελικά θα πρέπει να είμαστε σε θέση να φτιάξουμε μια «γάτα» αρκετά «μεγάλη» ώστε τα κυματοπακέτα που περιγράφουν τις δύο διαφορετικές καταστάσεις της γάτας να διαχωρίζονται από μακροσκοπικές αποστάσεις[13].
Η ΓΑΤΑ ΤΟΥ CHESHIRE
H Γάτα του Cheshire έγινε παγκοσμίως γνωστή από το διάσημο έργο του Lewis Caroll Η Αλίκη στη χώρα των θαυμάτων. Αυτό το φανταστικό ον χαρακτηριζόταν από ένα αεικίνητο χαμόγελο που μπορούσε να αποσπασθεί από το σώμα της γάτας και να παραμένει κάπου στον χώρο ενώ η γάτα είχε εξαφανισθεί. Oι κβαντικές Γάτες του Cheshire προτάθηκαν για πρώτη φορά το 2013 από τους Yakir Aharonov, Sandu Popescu, Daniel Rohrlich και Paul Skrzypczyk σε ένα άρθρο που δημοσιεύτηκε το 2013 (Aharonov et al, 2013). Πρόκειται για ένα εντελώς αντιδιαισθητικό φαινόμενο στο οποίο μια φυσική ιδιότητα του σωματιδίου μπορεί να βρεθεί σε εντελώς διαφορετικό σημείο του χώρου από το σωματίδιο! Στη βάση αυτού του φαινομένου βρίσκονται οι ασθενείς κβαντικές μετρήσεις, στις οποίες αναφερθήκαμε στην αρχή του άρθρου, και οι οποίες άνοιξαν την πόρτα ενός εντελώς νέου κόσμου από κβαντικά φαινόμενα στους ερευνητές.
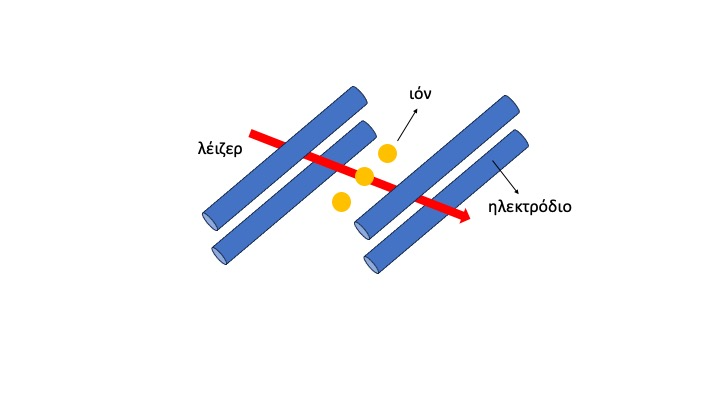
Στο άρθρο του 2013, ο Aharonov και συνεργάτες φαντάστηκαν μια απλή διάταξη οπτικού συμβολόμετρου, στην οποία η «γάτα» είναι ένα φωτόνιο που μπορεί να βρίσκεται είτε στο αριστερό είτε στο δεξί σκέλος, ενώ το «χαμόγελο» είναι η κυκλική του πόλωση (Εικ.5). Η γάτα (το φωτόνιο) προετοιμάζεται πρώτα σε μια υπέρθεση δύο δυνατών διαφορετικών καταστάσεων: ή να ταξιδέψει προς τα αριστερά είτε προς τα δεξιά. Η πειραματική αυτή φάση είναι γνωστή ως προ-επιλογή (pre-selection). Από εκεί και πέρα αναλαμβάνουν οι ασθενείς μετρήσεις. Αντί για μια απευθείας μέτρηση στο φωτόνιο, η οποία θα κατέστρεφε την πολύτιμη υπέρθεση που επιτεύχθηκε στην πρώτη φάση, εκτελούνται στο σύστημα μια σειρά ασθενείς μετρήσεις. Στο τέλος γίνεται χρήση της λεγόμενης μετα-επιλογής (post-selection) όπου επιλέγονται μόνο οι περιπτώσεις που το φωτόνιο καταλήγει σε μια συγκεκριμένη κατάσταση. Αυτό επιτρέπει στους ερευνητές την ακόλουθη συνεπαγωγή: όταν το φωτόνιο περνάει μέσα από την συμβολομετρική διάταξη αυτό αποτελεί ένδειξη πως το φωτόνιο έχει καταγραφεί στα αριστερά και η πόλωσή του στα δεξιά. Αν δεν γίνει αυτή η μετά-επιλογή θα πρέπει να γίνει ένας μέσος όρος σε όλα τα πιθανά αποτελέσματα και το παράδοξο φαινόμενο εξαφανίζεται. Ο λόγος που αυτό συμβαίνει είναι η ίδια η φύση των ασθενών μετρήσεων που δεν δίνουν ρητές απαντήσεις όπως μια συνήθης κβαντική μέτρηση αλλά οδηγούν το σύστημα να αφήνει τα «ίχνη» του, από την στατιστική επεξεργασία των οποίων οι ερευνητές καταλήγουν στην συγκρότηση της εικόνας για την κατάσταση του συστήματος.
Εικ. 5. Σχηματική αναπαράσταση της διάταξης που χρησιμοποιήθηκε από τον Aharonov και τους συνεργάτες του (Aharonov et al, 2013).
Η μαθηματική περιγραφή αυτής της παράξενης κατάστασης πραγμάτων ήταν ξεκάθαρη, αλλά η ερμηνεία φάνηκε εξωφρενική και το αρχικό άρθρο πέρασε πάνω από έναν χρόνο σε αξιολόγηση, με τη δημοσίευσή του να προκαλεί ακόμη κριτικές. Λίγο αργότερα, πειράματα με πολωμένα νετρόνια (Denkmayr, et al, 2014) και φωτόνια (Ashby, et al, 2016) δοκίμασαν και επιβεβαίωσαν τα αποτελέσματα του πρώτου πειράματος. Ωστόσο, τα πειράματα αυτά και οι επόμενες δοκιμές, παρά την επιβεβαίωση των θεωρητικών προβλέψεων, δεν έκλεισαν τη συζήτηση – τελικά, το ζήτημα ήταν στην ερμηνεία.
Εικ. 6. Συστήματα και αντίστοιχες ιδιότητες που μπορούν να χρησιμοποιηθούν ως Γάτες του Cheshire και «χαμόγελα».
Για να κατανοήσει κανείς αυτή την παράξενη κατάσταση θα πρέπει να καταφύγει σε ένα δημοφιλές παιγνίδι της Ιαπωνίας, το pachinko, που η λειτουργία του είναι αρκετά κοντά στις έννοιες της προ- και μετα-επιλογής. Πρόκειται για μια μηχανή, κάτι σαν ένα κατακόρυφο φλίπερ, όπου μια μπίλια ξεκινά από την κορυφή σε ένα επιλεγμένο σημείο (προ-επιλογή) και πέφτει μέσω εμποδίων καταλήγοντας σε μια συγκεκριμένη έξοδο (jackpot, μετα-επιλογή) την οποία πρέπει να προβλέψεις και να στοιχηματίσεις. Μετρώντας πόσες μπίλιες καταλήγουν σε όλες τις εξόδους/jackpot, μπορείς να υπολογίσεις την κατανομή πιθανότητας. Στον κλασικό κόσμο, η μέτρηση της θέσης και των ιδιοτήτων της μπίλιας σε διάφορα σημεία είναι δυνατή χωρίς να επηρεάζεται η πορεία της. Σε μια κβαντική εκδοχή της μηχανής, η προ- και μετα-επιλογή λειτουργούν παρόμοια, εκτός του ότι μπορείς να τροφοδοτήσεις το σύστημα με καταστάσεις υπέρθεσης. Μια ασθενής μέτρηση δεν διαταράσσει το σύστημα, οπότε μπορεί να γίνει επανειλημμένα για να εξαχθούν πιθανότητες συγκεκριμένων αποτελεσμάτων. Το αποτέλεσμα της μέτρησης δεν θα είναι ιδιοτιμή – δηλαδή πραγματική ιδιότητα του συστήματος αλλά ασθενής τιμή, η οποία δεν έχει ξεκάθαρη ερμηνεία.
Από την αρχική ανακάλυψη και μετά, οι Aharonov, Popescu και συνεργάτες έχουν συναντήσει και άλλες εκπλήξεις. Το 2021 γενίκευσαν το φαινόμενο της κβαντικής Γάτας του Cheshire σε ένα δυναμικό πλαίσιο στο οποίο η «διαχωρισμένη» ιδιότητα μπορεί να διαδίδεται στον χώρο (Duprey, et al, 2021). Για παράδειγμα, μπορεί να υπάρξει ροή στροφορμής χωρίς τίποτα να τη μεταφέρει (Atherton et al, 2016). Σε μια άλλη γενίκευση, ο Aharonov φαντάστηκε ένα σωματίδιο με μάζα που μπορεί να μετρηθεί σε ένα σημείο χωρίς ορμή, ενώ η ορμή του μετριέται αλλού χωρίς τη μάζα του (Waegell, et al, 2024).
Η κατανόηση αυτού του φαινομένου έχει σηκώσει μεγάλη συζήτηση στην επιστημονική κοινότητα ενώ ήδη έχουν εμφανιστεί οι πρώτες αντιρρήσεις σχετικά με την ερμηνεία των αποτελεσμάτων των πειραμάτων που έχουν διεξαχθεί. Μια πρόσφατη έρευνα δείχνει ότι αυτά τα πειράματα δεν δείχνουν στην πραγματικότητα σωματίδια που αποσπώνται από τις ιδιότητές τους, αλλά αντιθέτως εμφανίζουν ένα άλλο αντιφατικό χαρακτηριστικό της κβαντομηχανικής – την πλαισιακή (contextual) φύση της (Hance et al, 2023). Δηλαδή το γεγονός πως τα κβαντικά συστήματα μεταβάλλονται ανάλογα με τις μετρήσεις που εκτελούμε σε αυτά[14]. Μια ακολουθία μετρήσεων σε ένα κβαντικό σύστημα θα παράγει διαφορετικά αποτελέσματα ανάλογα με τη σειρά με την οποία εκτελούνται οι μετρήσεις. Για παράδειγμα, αν μετρήσουμε πού βρίσκεται ένα σωματίδιο και στη συνέχεια πόσο γρήγορα ταξιδεύει, αυτό θα δώσει διαφορετικά αποτελέσματα από το να μετρήσουμε πρώτα πόσο γρήγορα ταξιδεύει και στη συνέχεια πού βρίσκεται. Λόγω αυτού του πλαισιακού χαρακτήρα, τα κβαντικά συστήματα μπορούν να μετρηθούν ως έχοντα ιδιότητες που θα περιμέναμε να είναι αμοιβαία ασύμβατες.
Η ομάδα που δημοσίευσε την εργασία σημειώνει ότι το πρόβλημα με το κβαντικό παράδοξο της Γάτας του Cheshire είναι ότι ο αρχικός ισχυρισμός του, ότι το σωματίδιο και η ιδιότητά του, όπως το σπιν ή η πόλωση, διαχωρίζονται και ταξιδεύουν σε διαφορετικές διαδρομές, αποτελεί, ίσως, μια παραπλανητική αναπαράσταση της πραγματικής φυσικής της κατάστασης. Οι ερευνητές πιστεύουν πως διαφορετικά αποτελέσματα λαμβάνονται εάν ένα κβαντικό σύστημα μετρηθεί με διαφορετικούς τρόπους και ότι η αρχική ερμηνεία της κβαντικής γάτας του Cheshire προκύπτει μόνο εάν συνδυάσουμε τα αποτελέσματα αυτών των διαφορετικών μετρήσεων με έναν πολύ συγκεκριμένο τρόπο και αγνοήσουμε αυτήν την αλλαγή που σχετίζεται με τη μέτρηση. Θεωρούν επίσης πως η συνέχιση της έρευνας πάνω στο ζήτημα της πλαισίωσης πέρα από την επίλυση θεωρητικών προβλημάτων θα μπορεί να αξιοποιηθεί και για πρακτικούς σκοπούς καθώς θα οδηγήσει σε πληρέστερη αξιοποίηση των δυνατοτήτων της κβαντικής υπολογιστικής.
ΣΥΜΠΕΡΑΣΜΑΤΑ
Οι Γάτες της κβαντομηχανικής δεν εξάπτουν μόνο την περιέργεια και την φαντασία αλλά αποτελούν πλέον, μαζί με άλλα νοητικά πειράματα, μια πραγματικότητα που έχει αναδειχθεί από πλήθος πειραμάτων στα ανά τον κόσμο εργαστήρια. Σήμερα έχουμε τη δυνατότητα να πειραματιστούμε με μεμονωμένα ή ολιγάριθμα κβαντικά συστήματα, προετοιμάζοντας ντετερμινιστικά υπερθέσεις και σύμπλεκτες υπερθέσεις των καταστάσεων τους. Σίγουρα ο έλεγχός μας είναι καλύτερος όταν έχουμε να κάνουμε με πολύ μικρό αριθμό σωματιδίων, κάτι που μας επιτρέπει να πραγματοποιήσουμε πολλά από τα νοητικά πειράματα που παρείχαν τη βάση για τις συζητήσεις/αντιπαραθέσεις μεταξύ του Schrödinger και των άλλων θεμελιωτών της κβαντομηχανικής. Και φυσικά είμαστε σε θέση να φτιάξουμε «μικρές» εκδοχές της Γάτας του Schrödinger ή αυτής του Cheshire, οι οποίες δεν είναι σε καμία περίπτωση μακροσκοπικές αλλά έχουν τα ίδια βασικά χαρακτηριστικά. Μέχρι στιγμής, φαίνεται ότι η αδυναμία μας να δημιουργήσουμε μακροσκοπικές «γάτες» οφείλεται μόνο σε τεχνικούς και όχι σε θεμελιώδεις περιορισμούς. Ομολογουμένως, αυτοί οι τεχνικοί περιορισμοί είναι αρκετά ισχυροί, αλλά μπορεί κανείς να είναι αισιόδοξος για την αύξηση του μεγέθους αυτών των καταστάσεων καθώς η τεχνολογία συνεχίζει να βελτιώνεται. Παρεπιπτόντως, πρέπει να σημειώσουμε πως η διαρκής αύξηση του μεγέθους μιας κβαντικής «γάτας» πέρα από το ζήτημα της φύσης της κβαντικής μέτρησης συνδέεται οργανικά και με ένα άλλο «ιερό δισκοπότηρο» της σημερινής έρευνας: την ανάδυση του κλασικού κόσμου μέσα από τον κβαντικό. Με άλλα λόγια, τη διαύγαση του ορίου πέρα από το οποίο η συμπεριφορά ενός συστήματος παύει να περιγράφεται από τους νόμους της κβαντομηχανικής και βρίσκεται πλέον στην επικράτεια της κλασικής φυσικής (Arndt et al., 1999).
Αυτό που αρκετοί ερευνητές θεωρούν ως το πιο πολύτιμο παράγωγο αυτών των πειραματικών προσπαθειών είναι η ώθηση που σου δίνουν να σκέφτεσαι διαρκώς «εκτός πλαισίου» (out of the box) ακόμη και αν οι άμεσες εφαρμογές δεν είναι προφανείς. Όπως έχει τονίσει ο φυσικός Jonte Hance, ερευνητής στα θεμέλια της κβαντικής θεωρίας στο Πανεπιστήμιο του Νιούκαστλ, οι ερευνητές «τείνουν να ξεχνούν πόσο παράξενη είναι η κβαντική μηχανική, και για εμένα είναι απαραίτητο να κρατήσουμε αυτή τη διαίσθηση της παραξενιάς της» ενώ ο εκ των πρωταγωνιστών του χώρου Popescu θα συμπληρώσει, «Οι περισσότεροι συμφωνούν ότι, αν και γνωρίζουμε τους βασικούς νόμους της κβαντικής μηχανικής, δεν καταλαβαίνουμε πραγματικά περί τίνος πρόκειται».
Κλείνοντας το άρθρο αξίζει να αναφέρουμε πως το ενδιαφέρον των ερευνητών για την πειραματική διερεύνηση των θεμελίων της κβαντομηχανικής δεν ήταν πάντα δεδομένο[15]. Οι επιστήμονες ήταν συνήθως και κατά κύριο λόγο απασχολημένοι με τις εφαρμογές της κβαντομηχανικής και αυτή η τάση είναι ακόμη πιο ισχυρή στις ημέρες μας με την διαφαινόμενη εμπορική εκμετάλλευση των νέων κβαντικών τεχνολογιών, όπως οι κβαντικοί υπολογιστές και η κβαντική κρυπτογραφία. Στα πλαίσια αυτού του «πυρετού» έχει αναγεννηθεί το ενδιαφέρον για έρευνα στα θεμέλια της κβαντομηχανικής.
ΣΗΜΕΙΩΣΕΙΣ
[1] Πρόκειται για τη συνάρτηση που μας παρέχει την μέγιστη δυνατή πληροφορία που μπορεί να εξαχθεί πειραματικά για τη φυσική κατάσταση του συστήματος. ↩
[2] Με την έννοια πως το σύνολο των πιθανών αποτελεσμάτων είναι δεδομένο (όχι όμως το αποτέλεσμα μιας μεμονωμένης μέτρησης) και αλλάζει εάν μεταβληθούν με κάποιο τρόπο τα χαρακτηριστικά του συστήματος. ↩
[3] Πρόκειται για την αρχή της κβαντομηχανικής η οποία προβλέπει πως δύο σύμπλεκτα συστήματα δεν μπορούν να αποσυμπλεχθούν (δηλαδή, δεν μπορούν να χάσουν όλες τις συσχετίσεις που προκύπτουν από την κβαντική σύμπλεξη) εκτός εάν υπόκεινται σε εξωτερική αλληλεπίδραση. Σύμφωνα με αυτή την κβαντομηχανική αρχή, δύο ή περισσότερα σωματίδια που είναι εμπλεκόμενα συμπεριφέρονται ως ένα ενιαίο φυσικό αντικείμενο, ανεξάρτητα από την απόσταση μεταξύ τους. ↩
[4] Πρόκειται για την αρχή της κβαντομηχανικής η οποία προβλέπει πως τα φυσικά συστήματα χαρακτηρίζονται από φυσικά μεγέθη τα οποία δεν μπορούν να μετρηθούν ταυτόχρονα, όπως για παράδειγμα η θέση και η ορμή ενός σωματιδίου. ↩
[5] Για παράδειγμα, στο άτομο του ρουβιδίου (Rb), ένα ηλεκτρόνιο ευρισκόμενο στην κατάσταση Rydberg με κύριο κβαντικό αριθμό 𝑛=50 βρίσκεται σε απόσταση περίπου 132 nm από τον πυρήνα. Αντίθετα, το ηλεκτρόνιο σθένους της θεμελιώδους κατάστασης που καταλαμβάνει το τροχιακό 5s βρίσκεται σε απόσταση περίπου 1.32 nm από τον πυρήνα ↩
[6] Ο όρος καθιερώθηκε από τον D. Kleppner στις αρχές της δεκαετίας του 1980. ↩
[7] Ιδαίτερη αναφορά αξίζει στην κατασκευή του λεγόμενου μικρομέιζερ (micromaser) από την ερευνητική ομάδα του H. Walther στο Max Planck Institut στο Garching της Δ. Γερμανίας. Στέλνοντας άτομα Rydberg, ένα κάθε φορά, μέσα από μια ηλεκτρομαγνητική κοιλότητα, δημιούργησαν ένα μέιζερ στο οποίο το πεδίο έφτανε σε σταθερή κατάσταση μέσα από μια σειρά από διαδοχικές δράσεις μεμονωμένων ατόμων που διέσχιζαν τη κοιλότητα ένα προς ένα [31] ↩
[8] O αναγνώστης που επιθυμεί να γνωρίσει όλη την πορεία από τα πρώιμα πειράματα σε ηλεκτρομαγνητικές κοιλότητες μπορεί να διαβάσει το Haroche, S. and Kleppner, D., 1989. Cavity quantum electrodynamics. Physics Today, 42(1), pp.24-30, https://pubs.aip.org/physicstoday/article-abstract/42/1/24/405477/Cavity-Quantum-ElectrodynamicsA-new-generation-of. ↩
[9] Στην κβαντική μηχανική εάν έχουμε δύο συμπληρωματικά φυσικά μεγέθη (όπως το ζεύγος θέση-ορμή) 𝛢 και 𝛣, το γινόμενο των τυπικών αποκλίσεών τους Δ𝛢𝛢και Δ𝛣 ικανοποιεί την ανισότητα Δ𝛢∙Δ𝛣≥ℎ/2𝜋𝜋, όπου ℎ η σταθερά του Planck. ↩
[10] Το φως του λέιζερ πάνω από το κατώφλι λειτουργίας είναι ένα παράδειγμα μιας σύμφωνης κατάστασης. Εν γένει αν ένα κβαντικό σύστημα διεγερθεί από ένα εξωτερικό κλασικό πεδίο μεταπίπτει από τη θεμελιώδη κατάστασή του σε μια σύμφωνη κατάσταση. Για παράδειγμα αν στείλουμε φως λέιζερ σε μια ηλεκτρομαγνητική κοιλότητα το πεδίο της μεταπίπτει σε μια σύμφωνη κατάσταση ή αν ασκήσουμε μια δύναμη σε έναν αρμονικό κβαντικό ταλαντωτή. ↩
[11] Στα πειράματα αυτά και στο φάσμα του φθορισμού παρατηρήθηκαν για άλλη μια φορά τα περίφημα κβαντικά άλματα (quantum jumps). ↩
[12] Σε μια πιο αυστηρή επιστημονικά γλώσσα κάτι τέτοιο το επιτρέπει ο μποζονικός χαρακτήρας των καταστάσεων του κβαντωμένου ηλεκτρομαγνητικού πεδίου όσο και του κβαντικού αρμονικού ταλαντωτή. ↩
[13] Η θεωρητική ανάλυση δείχνει ότι η αλληλεπίδραση με το περιβάλλον επιφέρει ταχύτατη απώλεια του σύμφωνου χαρακτήρα της δυναμικής της «γάτας». Ο W. Zurek έχει παίξει σημαντικό ρόλο στη διαλεύκανση του ρόλου του περιβάλλοντος σε αυτή τη διαδικασία, η οποία συμβαίνει όλο και πιο γρήγορα καθώς το «μέγεθος» της «γάτας» αυξάνεται (Zurek, 1991). ↩
[14] Πιο αυστηρά, το αποτέλεσμα μιας μέτρησης (υποτιθέμενο ως προϋπάρχον) ενός κβαντικού παρατηρήσιμου εξαρτάται από το ποια άλλα μετατιθέμενα με αυτό παρατηρήσιμα μεγέθη βρίσκονται εντός του ίδιου συνόλου μετρήσεων (Kochen & Specker, 1990). ↩
[15] Η έλλειψη ενδιαφέροντος για τα θεμέλια της κβαντικής θεωρίας αποτυπώνεται χαρακτηριστικά σε δύο ανέκδοτα. Το πρώτο με πρωταγωνιστή τον ίδιο τον Aharonov. Όταν σπούδαζε φυσική στο Τεχνολογικό Ινστιτούτο του Ισραήλ (Technion) τη δεκαετία του 1950, ρώτησε τον Nathan Rosen (το R του περίφημου παράδοξου EPR, στο Einstein et al. 1935) αν μπορούσε να εργαστεί στα θεμέλια της κβαντικής μηχανικής. Το θέμα θεωρήθηκε τόσο μη δημοφιλές, που ο Rosen τον συμβούλεψε να επικεντρωθεί στις εφαρμογές (Berry, 1997). Ευτυχώς, ο Aharonov αγνόησε τη συμβουλή και συνεργάστηκε με τον Αμερικανό θεωρητικό David Bohm. Η άλλη ιστορία αφορά τον Alain Aspect, ο οποίος το 1975 επισκέφθηκε τον φυσικό του CERN John Bell για να ζητήσει συμβουλές σχετικά με τα σχέδιά του να πραγματοποιήσει πείραμα για τις ανισότητες του Bell ώστε να ελέγξει το παράδοξο EPR. Η πρώτη ερώτηση του Bell δεν αφορούσε τις λεπτομέρειες του πειράματος – αλλά το αν ο Aspect είχε μόνιμη θέση εργασίας (Nature 18, 961, 2002). Ευτυχώς, είχε, και έτσι εκτέλεσε το πείραμα, το οποίο του χάρισε μέρος του Νόμπελ Φυσικής το 2022 (Aspect et al., 1982; Aspect, 2007). ↩
ΕΥΧΑΡΙΣΤΙΕΣ
Ευχαριστώ πολύ τον Κωνσταντίνο Ταμπάκη,κύριο ερευνητή στην Ιστορία των Επιστημών και της Τεχνολογίας στο Ινστιτούτο Ιστορικών Ερευνών του Εθνικού Ιδρύματος Ερευνών και τον Θόδωρο Αραμπατζή,καθηγητή ιστορίας και φιλοσοφίας της επιστήμης στο Πανεπιστήμιο της Αθήνας, για τις πολύτιμες παρατηρήσεις τους πάνω στο αρχικό κείμενο.
ΒΙΒΛΙΟΓΡΑΦΙΑ
ΕΛΛΗΝΙΚΗ
Τραχανάς, Σ. (2009). ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ ΙΙ. Θεμελιώδεις Αρχές και Μέθοδοι – Κβαντικοί Υπολογιστές. Ηράκλειο: ΠΕΚ.
ΞΕΝΟΓΛΩΣΣΗ
Aharonov, Y., Popescu, S., Rohrlich, D. & Skrzypczyk, P., 2013. Quantum Cheshire Cats. New Journal of Physics, 15, 113015. https://doi.org/10.1088/1367-2630/15/11/113015
Ashby, J. M., Schwarz, P. D. and Schlosshauer, M., 2016. Observation of the quantum paradox of separation of a single photon from one of its properties. Physical Review A, 94(1), p.012102. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.94.012102
Aspect, A., Grangier, P. and Roger, G., 1982. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: a new violation of Bell’s inequalities. Physical Review Letters, 49(2), p.91. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.49.91
Aspect, A. (2007). Bell’s inequality test: more ideal than ever. Nature Physics, 3, 674–675. https://doi.org/10.1038/nphys722
Atherton, D. P. et al. (2016). Observation of the quantum Cheshire Cat effect with polarization-entangled photons. Physical Review A, 94(1), 012102. https://doi.org/10.1103/PhysRevA.94.012102
Arndt, M., Nairz, O., Vos-Andreae, J., Keller, C., Van der Zouw, G. and Zeilinger, A., 1999. Wave–particle duality of C60 molecules. Nature, 401(6754), pp.680-682. https://doi.org/10.1038/44348
Berry, M., 1997. Oration delivered by Michael Berry for Yakir Aharonov. https://michaelberryphysics.wordpress.com/wp-content/uploads/2013/06/u11.pdf
Braginsky, V. B. and Khalili, F. Y., 1996. Quantum nondemolition measurements: the route from toys to tools. Reviews of Modern Physics, 68(1), p.1. https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.68.1
Deleglise, S., Dotsenko, I., Sayrin, C., Bernu, J., Brune, M., Raimond, J. M., & Haroche, S., (2008). Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature, 455(7212), 510-514. https://pubmed.ncbi.nlm.nih.gov/18818653/
Denkmayr, T., Geppert, H., Sponar, S., Lemmel H., Matzkin A., Tollaksen, J., and Hasegawa., J., (2014). Observation of a quantum Cheshire Cat in a matter-wave interferometer experiment’, Nature Communications, 5, p. 4492. 10.1038/ncomms5492
Duprey, Q., Aharonov, Y., Popescu, S., & Tollaksen, J., 2021. Dynamical Quantum Cheshire Cats. Nature Communications, 12, 4770. https://doi.org/10.1038/s41467-021-25053-8
Einstein, A., Podolsky, B., & Rosen, N., 1935. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47, 777. https://doi.org/10.1103/PhysRev.47.777
Hance, J. R., Ji, M. and Hofmann, H. F., 2023. Contextuality, coherences, and quantum cheshire cats. New Journal of Physics, 25(11), p.113028. https://iopscience.iop.org/article/10.1088/1367-2630/ad0bd4
Haroche, S. & Raimond, J. M. (2006) Exploring the Quantum: Atoms, Cavities, and Photons. Oxford: Oxford University Press.
Haroche, S., 2013. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Reviews of Modern Physics, 85(3), pp.1083-1102. https://doi.org/10.1103/RevModPhys.85.1083
Jhe, W., Anderson, A., Hinds, E. A., Meschede, D., Moi, L. and Haroche, S., 1987. Suppression of spontaneous decay at optical frequencies: Test of vacuum-field anisotropy in confined space. Physical Review Letters, 58(7), p.666. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.58.666
Kochen, S. and Specker, E. P., 1990. The problem of hidden variables in quantum mechanics. Ernst Specker Selecta, pp.235-263. https://doi.org/10.1007/978-3-0348-9259-9_21
Lembessis, V. E., 2020. Taming Atoms: The Renaissance of Atomic Physics. Bellingham, Washington USA: SPIE. https://spie.org/Publications/Book/2563827?SSO=1
Monroe, C., Meekhof, D.M., King, B.E. and Wineland, D.J., 1996. A “Schrödinger cat” superposition state of an atom. science, 272(5265), pp.1131-1136. https://www.
Monroe, C. R. and Wineland, D. J., 2008. Quantum computing with ions. Scientific American, 299(2), pp.64-71. https://www.jstor.org/stable/26000763
Myatt, C. J., King, B. E., Turchette, Q. A., Sackett, C. A., Kielpinski, D., Itano, W. M., Monroe, C. and Wineland, D. J., 2000. Decoherence of motional states of trapped ions. Journal of Modern Optics, 47(12), pp.2181-2186. https://doi.org/10.1080/09500340008235140
Myatt, C. J., King, B. E., Turchette, Q. A., Sackett, C. A., Kielpinski, D., Itano, W. M., Monroe, C. W. D. J. and Wineland, D. J., 2000. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature, 403(6767), pp.269-273. https://www.nature.com/articles/35002001
Neuhauser, W., Hohenstatt, M., Toschek, P.E. and Dehmelt, H., 1980. Localized visible Ba+ mono-ion oscillator. Physical Review A, 22(3), p.1137. https://journals.aps.
Saffman, M. (2016) ‘Quantum computing with atomic qubits and Rydberg interactions’, Journal of Physics B: Atomic, Molecular and Optical Physics, 49(20), p. 202001. 10.1088/0953-4075/49/20/202001
Schrödinger, Ε., 1935. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 844. https://link.springer.com/article/10.1007/BF01491891
Schrödinger, E., 1952. Are there quantum jumps? Part I. The British Journal for the Philosophy of science, 3(10), pp.109-123. https://www.journals.uchicago.edu/doi/abs/10.1093/bjps/III.10.109?journalCode=bjps
Turchette, Q. A., Myatt, C. J., King, B. E., Sackett, C. A., Kielpinski, D., Itano, W. M., Monroe, C. and Wineland, D. J., 2000. Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs. Physical Review A, 62(5), p.053807. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.62.053807
Waegell, M., Tollaksen, J. and Aharonov, Y., 2024. Separating a particle’s mass from its momentum. Quantum, 8, p.1536. https://quantum-journal.org/papers/q-2024-11-26-1536/
Wineland, D. J., 2013. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Reviews of Modern Physics, 85(3), pp.1103-1114. https://doi.org/10.1103/RevModPhys.85.1103
Zurek, W. H., 1991. Decoherence and the transition from quantum to classical. Physics Today, 44(10), pp.36-44. https://pubs.aip.org/physicstoday/article-abstract/44/10/36/406457/Decoherence-and-the-Transition-from-Quantum-to