Ο δρόμος προς τα σύγχρονα θαύματα της μηχανικής μάθησης στρώθηκε με ιδέες από τη στατιστική μηχανική και τα συλλογικά φαινόμενα.
Johanna L. Miller
Μετάφραση: Δημήτρης Κούλος
Επιμέλεια μετάφρασης: Νικόλ Σαρλά, Βασίλης Λεμπέσης
Επιστημονική επιμέλεια: Βασίλης Λεμπέσης

«Ό,τι δίνεις παίρνεις».[1] Σύμφωνα με το παλιό ρητό της επιστήμης των υπολογιστών, αυτό που λαμβάνεις από έναν υπολογιστή δεν είναι καλύτερο από αυτό που του δίνεις. Και φαίνεται να υπονοεί ότι καθώς οι υπολογιστές δεν μπορούν να σκεφτούν μόνοι τους, δεν μπορούν ποτέ να κάνουν κάτι πιο εξεζητημένο από αυτό για το οποίο ρητώς τους έχει δοθεί εντολή.
Όμως, το τελευταίο φαίνεται να μην είναι πλέον αληθές. Τα νευρωνικά δίκτυα –αρχιτεκτονικές των υπολογιστών εμπνευσμένες από τον ανθρώπινο εγκέφαλο, στις οποίες τα σήματα διέρχονται μέσα από κόμβους που ονομάζονται τεχνητοί νευρώνες– έχουν παράγει τα τελευταία χρόνια κύματα εκπληκτικών αποτελεσμάτων. (Βλ. για παράδειγμα σελ. 17 αυτού του τεύχους.) Οι μεμονωμένοι νευρώνες εκτελούν μονάχα τους πλέον στοιχειώδεις υπολογισμούς. Όμως, όταν συγκεντρώνονται σε αρκετά μεγάλους αριθμούς και όταν τροφοδοτούνται με αρκετά δεδομένα προς εκπαίδευση, αποκτούν δυνατότητες που, φαινομενικά από το πουθενά, θυμίζουν απροσδόκητα την ανθρώπινη νοημοσύνη.
Οι φυσικοί δεν είναι ανοίκειοι με την ιδέα της ανάδυσης απροσδόκητων φαινομένων μέσα από απλούστερα δομικά στοιχεία. Μερικά στοιχειώδη σωματίδια και οι κανόνες των αλληλεπιδράσεών τους συνδυάζονται για να δώσουν σχεδόν το σύνολο του ορατού κόσμου: υπεραγωγοί, πλάσματα και όλα τα ενδιάμεσα. Γιατί κάποια προσέγγιση της φυσικής στην αναδυόμενη πολυπλοκότητα να μην εφαρμοστεί και στα νευρωνικά δίκτυα;
Πράγματι εφαρμοζόταν –και συνεχίζει να εφαρμόζεται– όπως αποδεικνύεται από το φετινό (2024) βραβείο Νόμπελ Φυσικής, το οποίο απονέμεται στον John Hopfield του Πανεπιστημίου του Πρίνστον και στον Geoffrey Hinton του Πανεπιστημίου του Τορόντο. Ξεκινώντας στις αρχές της δεκαετίας του 1980, ο Hopfield έθεσε τα εννοιολογικά θεμέλια για μια θεώρηση που να βασίζεται στη φυσική του ζητήματος της επεξεργασίας πληροφοριών η οποία εμπνέεται από την λειτουργία του εγκέφαλου· ο Hinton ήταν στην πρώτη γραμμή της προσπάθειας δεκαετιών για την αξιοποίηση αυτών των ιδεών για να αναπτύξει αλγορίθμους που χρησιμοποιούνται σήμερα από τα μοντέλα νευρωνικών δικτύων.
ΥΑΛΩΔΗΣ ΜΝΗΜΗ
Στην αρχή δεν ήταν καθόλου προφανές ότι τα νευρωνικά δίκτυα θα γίνονταν τόσο ισχυρά. Μόλις το 2011, τα πιο εντυπωσιακά επιτεύγματα στην τεχνητή νοημοσύνη επιτυγχάνονταν από μια εντελώς διαφορετική προσέγγιση. Ο υπολογιστής Watson της IBM, που νίκησε τον Ken Jennings και τον Brad Rutter στο Jeopardy!,[2] δεν ήταν ένα νευρωνικό δίκτυο καθώς είχε προγραμματιστεί ρητώς με κανόνες για την επεξεργασία της γλώσσας, την ανάκτηση πληροφοριών και τη λογική σκέψη. Και πολλοί ερευνητές πίστεψαν ότι αυτός ήταν ο δρόμος για να δημιουργήσουν χρήσιμες μηχανές τεχνητής νοημοσύνης.
Αντίθετα, η πρώιμη εργασία για τα νευρωνικά δίκτυα ήταν μια έρευνα που καθοδηγούνταν από την περιέργεια, εμπνευσμένη περισσότερο από πραγματικούς εγκεφάλους παρά από τους υπολογιστές και τις εφαρμογές τους. Αλλά η φύση της διεπιστημονικής σύνδεσης ήταν δυσδιάκριτη. «Τα ερωτήματα που διατύπωσε ο Hopfield δεν είναι άσχετα με πράγματα που απασχολούσαν τους νευροεπιστήμονες», λέει ο William Bialek από το Πανεπιστήμιο του Πρίνστον. «Όμως δεν πρόκειται για “εφαρμογή της φυσικής στο τάδε ζήτημα’’· μάλλον πρόκειται για την εισαγωγή μιας ολόκληρης θεώρησης που απλώς δεν υπήρχε προηγουμένως».
Μέχρι τη δεκαετία του 1980, οι νευροεπιστήμονες γνώριζαν ότι ο εγκέφαλος αποτελείται από νευρώνες, οι οποίοι συνδέονται μεταξύ τους μέσω συνάψεων και εναλλάσσονται μεταξύ περιόδων υψηλής και χαμηλής ηλεκτρικής δραστηριότητας (στην καθομιλουμένη, “πυροδότηση” και “μη πυροδότηση”), και μελετούσαν συστήματα λίγων νευρώνων για να κατανοήσουν πώς η πυροδότηση ενός νευρώνα επηρέαζε εκείνους με τους οποίους συνδεόταν. «Κάποιοι αντιμετώπιζαν τους νευρώνες με όρους λογικών πυλών, όπως στην ηλεκτρονική», λέει ο Jay McClelland του Πανεπιστημίου του Στάνφορντ.
Σε μια εργασία-ορόσημο του 1982, ο Hopfield υιοθέτησε μια διαφορετική προσέγγιση.[3] Στη φυσική, υποστήριξε, πολλές σημαντικές ιδιότητες συστημάτων μεγάλης κλίμακας είναι ανεξάρτητες από τις λεπτομέρειες μικρής κλίμακας. Σε όλα τα υλικά μπορούν να διαδοθούν ηχητικά κύματα, για παράδειγμα, ανεξάρτητα από το πώς ακριβώς αλληλεπιδρούν τα άτομα ή τα μόριά τους. Οι μικροσκοπικές δυνάμεις μπορεί να επηρεάζουν την ταχύτητα του ήχου ή άλλες ακουστικές ιδιότητες, αλλά η μελέτη των δυνάμεων μεταξύ τριών ή τεσσάρων ατόμων αποκαλύπτει ελάχιστα για το πώς αναδύεται η έννοια των ηχητικών κυμάτων.
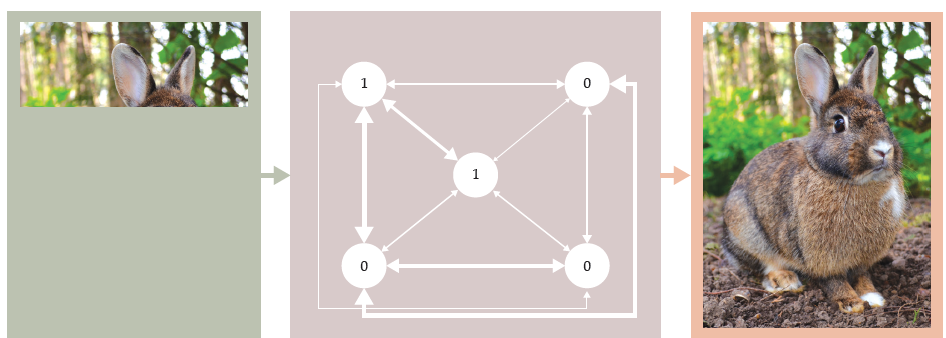
Με αυτόν τον τρόπο, δημιούργησε ένα μοντέλο ενός δικτύου νευρώνων, με γνώμονα περισσότερο την υπολογιστική και μαθηματική απλότητα παρά τον νευροβιολογικό ρεαλισμό. Το μοντέλο, γνωστό σήμερα ως δίκτυο Hopfield, αναπαρίσταται στο Εικ. 1. (Το σχήμα δείχνει ένα δίκτυο πέντε νευρώνων για την ευκολία της απεικόνισης· ο Hopfield προσομοίωνε δίκτυα 30 έως 100 νευρώνων). Κάθε νευρώνας μπορεί να βρίσκεται στην κατάσταση 1 ( πυροδότηση), ή στην κατάσταση 0 (μη πυροδότηση).
Η σύνδεση κάθε νευρώνα με όλους τους άλλους προσομοιωνόταν μέσω σταθερών σύζευξης που θα μπορούσαν να έχουν οποιαδήποτε θετική ή αρνητική τιμή, ανάλογα με το αν κάθε σύναψη ευνοεί ή όχι τους νευρώνες να πυροδοτούν ταυτόχρονα.
Αυτή είναι ακριβώς η ίδια μορφή με εκείνη ενός υαλώδους σπιν (spin glass), ένα γνωστό <<ακανθώδες>> σύστημα από τη φυσική συμπυκνωμένης ύλης. (Βλέπε Physics Today, Δεκέμβριος 2021, σ. 17.) Σε αντίθεση με ένα σιδηρομαγνήτη, στον οποίο οι σταθερές σύζευξης είναι όλες θετικές και το σύστημα έχει μια σαφή θεμελιώδη κατάσταση με όλα του τα σπιν ευθυγραμμισμένα, ένα υαλώδες σπιν δεν έχει σχεδόν ποτέ μια κατάσταση που να ικανοποιεί όλες τις ενεργειακές προτιμήσεις των σπιν του ταυτόχρονα. Το ενεργειακό του τοπίο είναι πολύπλοκο, με πολλά τοπικά ενεργειακά ελάχιστα.
Εικ. 1. Ένα δίκτυο Hopfield, τυπικά ισοδύναμο με ένα υαλώδες σπιν, λειτουργεί ως συνειρμική μνήμη: Όταν παρουσιάζεται μια κατάσταση που ανακαλείται μερικώς, χρησιμοποιεί έναν αλγόριθμο μείωσης της ενέργειας για να συμπληρώσει τα κενά. Οι αναμνήσεις αποθηκεύονται στην ισχύ των συζεύξεων μεταξύ των κόμβων. Όταν ο John Hopfield έδειξε ότι με τον κατάλληλο στατιστικό συνδυασμό στην ισχύ συζεύξεων το δίκτυο μπορούσε να αποθηκεύσει πολλές αναμνήσεις ταυτόχρονα, έθεσε τις βάσεις για τη σκέψη των νευρωνικών δικτύων με βάση τη φυσική. (Σχήμα από τον Freddie Pagani· φωτογραφία λαγού από τον JM Ligero Loarte/Wikimedia Commons/CC BY 3.0.)
Ο Hopfield υποστήριξε ότι το τοπίο θα μπορούσε να χρησιμεύσει ως μνήμη, με κάθε μια από τις διατάξεις που ελαχιστοποιούν την ενέργεια να χρησιμεύει ως μια κατάσταση που πρέπει να κρατηθεί στη μνήμη. Και παρουσίασε έναν κομψό τρόπο ρύθμισης των τιμών των σταθερών σύζευξης –εμπνευσμένο από αυτό που συμβαίνει στις πραγματικές συνάψεις– έτσι ώστε η μνήμη να αποθηκεύει οποιαδήποτε επιθυμητή συλλογή καταστάσεων.
Αλλά το δίκτυο Hopfield είναι θεμελιωδώς διαφορετικό από μια συνηθισμένη μνήμη υπολογιστή. Σε έναν υπολογιστή, κάθε στοιχείο των δεδομένων που πρόκειται να αποθηκευτεί κωδικοποιείται ως συμβολοσειρά από άσους και μηδενικά σε ένα συγκεκριμένο σημείο και ανακαλείται πηγαίνοντας πίσω σε αυτό το σημείο και διαβάζοντας τη συμβολοσειρά. Σε ένα δίκτυο Hopfield, όλα τα στοιχεία αποθηκεύονται ταυτόχρονα στις τιμές των σταθερών της σύζευξης ολόκληρου του δικτύου. Και μπορούν να ανακληθούν συνειρμικά, δίνοντας στο δίκτυο ένα σημείο εκκίνησης που μοιράζεται μόνο μερικά χαρακτηριστικά με μία από τις καταστάσεις που θυμάται και επιτρέποντάς του να «ηρεμήσει» στο πλησιέστερο ενεργειακό ελάχιστο. Τις περισσότερες φορές, θα ανακαλέσει την επιθυμητή μνήμη. (Βλέπε επίσης τα άρθρα του Haim Sompolinsky, Physics Today, Δεκέμβριος 1988, σ. 70, και του John Hopfield, PHYSICS Today, Φεβρουάριος 1994, σ. 40).
Και τα δύο αυτά είναι γεγονότα που συμβαίνουν στους πραγματικούς εγκεφάλους. « Ήταν πειραματικά γνωστό ότι σε ανώτερα ζώα η εγκεφαλική δραστηριότητα ήταν καλά διασκορπισμένη και ενέπλεκε πολλούς νευρώνες», λέει ο Hopfield. Και η συνειρμική μνήμη είναι κάτι που έχετε βιώσει άμεσα, αν έχετε θυμηθεί ποτέ ένα τραγούδι που έχετε ξανακούσει, αφού ακούσατε ένα τυχαίο απόσπασμά του.
Το μοντέλο του Hopfield ήταν μια τεράστια απλοποίηση ενός πραγματικού εγκεφάλου. Οι πραγματικοί νευρώνες είναι ουσιαστικά δυναμικοί, δεν χαρακτηρίζονται από στατικές καταστάσεις και οι πραγματικές συζεύξεις των νευρώνων δεν είναι συμμετρικές. Αλλά, κατά κάποιον τρόπο, αυτές οι διαφορές ήταν χαρακτηριστικά, όχι σφάλματα: έδειξαν ότι η συλλογική, συνειρμική μνήμη ήταν ένα αναδυόμενο φαινόμενο μεγάλης κλίμακας, ανθεκτικό σε λεπτομέρειες μικρής κλίμακας.
ΜΑΘΑΙΝΟΝΤΑΣ ΠΩΣ ΝΑ ΜΑΘΑΙΝΕΙΣ
«Όχι μόνο ο Hopfield είναι ένας πολύ καλός φυσικός, αλλά και το μοντέλο Hopfield είναι από μόνο του εξαιρετική φυσική”, λέει ο Leo van Hemmen, από το Τεχνικό Πανεπιστήμιο του Μονάχου. Παρ΄όλα αυτά, η διατύπωσή του το 1982 άφησε πολλά ενδιαφέροντα ανοιχτά ερωτήματα. Ο Hopfield είχε επικεντρωθεί σε προσομοιώσεις για να δείξει πώς το σύστημα «ηρεμεί» σε ένα ενεργειακό ελάχιστο· θα μπορούσε το μοντέλο να δεχθεί μια πιο στιβαρή αναλυτική αντιμετώπιση; Πόσες καταστάσεις θα μπορούσε να θυμάται το μοντέλο και τι θα συνέβαινε αν υπερφορτωνόταν; Υπήρχαν καλύτεροι τρόποι καθορισμού του μεγέθους των σταθερών σύζευξης από αυτόν που πρότεινε ο Hopfield;
Αυτές τις ερωτήσεις, και άλλες, ανέλαβε μια πληθώρα ερευνητών με σπουδές στη φυσική, οι οποίοι εμπνεύστηκαν από το έργο του Hopfield και εισήλθαν στον τομέα των νευρωνικών δικτύων κατά τη δεκαετία του 1980. «Οι φυσικοί είναι ευπροσάρμοστοι, περίεργοι και αλαζόνες –με θετικό τρόπο», λέει ο Eytan Domany, του Ινστιτούτου Επιστημών Weizmann στο Ισραήλ. «Είναι πρόθυμοι να μελετήσουν διεξοδικά και στη συνέχεια να καταπιαστούν με ένα πρόβλημα που δεν έχουν ξαναδεί, αν είναι ενδιαφέρον. Και όλοι είναι ενθουσιασμένοι με την κατανόηση του εγκεφάλου».
Ένα άλλο μέρος της γοητείας ήταν ο τρόπος με τον οποίο ο Hopfield είχε πάρει ένα παραδοσιακό πρόβλημα φυσικής και το είχε αντιστρέψει. «Στα περισσότερα προβλήματα ενεργειακού τοπίου, σας δίνονται οι μικροσκοπικές αλληλεπιδράσεις και ρωτάτε: Ποια είναι η βασική κατάσταση; Ποια είναι τα τοπικά ελάχιστα; Ποιο είναι ολόκληρο το τοπίο;», λέει ο Haim Sompolinsky, του Εβραϊκού Πανεπιστημίου της Ιερουσαλήμ. «Η εργασία του 1982 έκανε το αντίθετο. Ξεκινάμε με τις βασικές καταστάσεις που θέλουμε: τις αναμνήσεις. Και ρωτάμε: Ποιες είναι οι μικροσκοπικές αλληλεπιδράσεις που θα τις υποστηρίξουν ως βασικές καταστάσεις;»
Από εκεί και πέρα, ήταν ένα μικρό εννοιολογικό άλμα το να ρωτήσουμε: τι γίνεται αν οι ίδιες οι τιμές των σταθερών σύζευξης μπορούν να εξελιχθούν στο δικό τους ενεργειακό τοπίο; Δηλαδή, αντί το σύστημα να είναι προγραμματισμένο εκ των προτέρων με παραμέτρους για την κωδικοποίηση συγκεκριμένων μνημών, να μπορεί να αυτοβελτιώνεται με τη μάθηση;
Η μηχανική μάθηση σε νευρωνικά δίκτυα είχε δοκιμαστεί και στο παρελθόν. Το perceptron –μια συσκευή που μοιάζει με νευρωνικό δίκτυο και ταξινομεί εικόνες σε απλές κατηγορίες, όπως κύκλους και τετράγωνα– χρονολογείται από τη δεκαετία του 1950. Όταν του δόθηκε μια σειρά από εικόνες για εκπαίδευση και ένας απλός αλγόριθμος για την επικαιροποίηση των συνδέσεων μεταξύ των νευρώνων του, μπορούσε τελικά να μάθει να ταξινομεί σωστά ακόμη και εικόνες που δεν είχε ξαναδεί.
Αλλά το perceptron δεν λειτουργούσε πάντα καθώς με τον τρόπο που ήταν δομημένο το δίκτυο, μερικές φορές δεν υπήρχε κανένας τρόπος να ρυθμιστούν οι τιμές των σταθερών σύζευξης για να εκτελέσει την επιθυμητή ταξινόμηση. «Όταν συνέβαινε αυτό, θα μπορούσατε να επαναλαμβάνετε (την λειτουργία) για πάντα και ο αλγόριθμος δεν θα συνέκλινε ποτέ», λέει ο van Hemmen. «Αυτό ήταν ένα μεγάλο σοκ». Χωρίς μια κατευθυντήρια αρχή για την χάραξη μιας πορείας προς τα εμπρός, το πεδίο είχε βαλτώσει.
ΒΡΙΣΚΟΝΤΑΣ ΚΟΙΝΟ ΤΟΠΟ
Ο Hinton δεν ήρθε στα νευρωνικά δίκτυα έχοντας υπόβαθρο στη φυσική. Αλλά ο συνεργάτης του, Terrence Sejnowski –ο οποίος είχε πάρει το διδακτορικό του από τον Hopfield το 1978– είχε τέτοιο υπόβαθρο. Μαζί, επέκτειναν το δίκτυο Hopfield σε κάτι που ονόμασαν μηχανή Boltzmann, η οποία επέκτεινε σημαντικά τις δυνατότητες του μοντέλου χρησιμοποιώντας ξεκάθαρα έννοιες της στατικής φυσικής.[4]
Στις προσομοιώσεις του ο Hopfield το 1982, είχε ουσιαστικά διερευνήσει το καθαρό έργο του υαλώδους σπιν σε μηδενική θερμοκρασία επιτρέποντας στο σύστημα να εξελίξει την κατάστασή του μόνο με τρόπους που θα μείωναν τη συνολική του ενέργεια. Με αυτόν τον τρόπο, όποια κι αν ήταν η αρχική κατάσταση, κατέληγε σε ένα κοντινό τοπικό ενεργειακό ελάχιστο και παρέμενε εκεί.
«Ο Τέρι και εγώ αρχίσαμε αμέσως να σκεφτόμαστε τη στοχαστική εκδοχή, με μη μηδενική θερμοκρασία», λέει ο Hinton. Αντί για έναν ντετερμινιστικό κανόνα μείωσης της ενέργειας, χρησιμοποίησαν έναν αλγόριθμο Monte Carlo που επέτρεπε στο σύστημα να μεταπηδά περιστασιακά σε μια κατάσταση υψηλότερης ενέργειας. Δοθέντος αρκετού χρόνου, μια στοχαστική προσομοίωση του δικτύου θα εξερευνούσε ολόκληρο το ενεργειακό τοπίο και θα κατέληγε σε μια κατανομή πιθανοτήτων Boltzmann, με όλες τις καταστάσεις χαμηλής ενέργειας –ανεξάρτητα από το αν είναι τοπικά ενεργειακά ελάχιστα– να αντιπροσωπεύονται με υψηλή πιθανότητα.
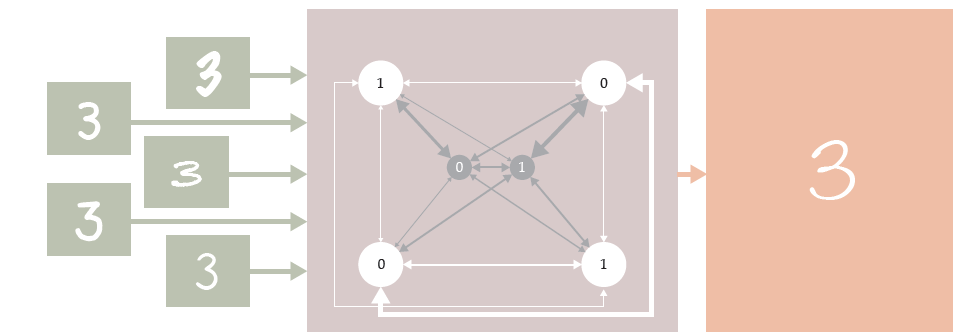
«Και το 1983, ανακαλύψαμε έναν πολύ όμορφο τρόπο για τη μάθηση», λέει ο Hinton. Όταν το δίκτυο τροφοδοτούνταν με δεδομένα για εκπαίδευση αυτά αναβάθμιζαν επαναληπτικά την τιμή των σταθερών σύζευξης, έτσι ώστε οι καταστάσεις των δεδομένων να έχουν υψηλή πιθανότητα στην κατανομή Boltzmann.[5] Επιπλέον, όταν τα εισερχόμενα δεδομένα είχαν κάτι κοινό –όπως οι εικόνες με τον αριθμόν 3 στην Εικ. 2– τότε άλλες καταστάσεις υψηλής πιθανότητας θα μοιράζονταν τα ίδια κοινά χαρακτηριστικά.
Εικόνα 2. Η ΜΗΧΑΝΗ BOLTZMANN επεκτείνει το δίκτυο Hopfield με δύο τρόπους: Επαυξάνει το δίκτυο για να συμπεριλάβει και κρυμμένους κόμβους (φαίνονται στο κέντρο του δικτύου με γκρι χρώμα) που δεν εμπλέκονται στην κωδικοποίηση δεδομένων και λειτουργεί σε μη μηδενική πραγματική θερμοκρασία, έτσι ώστε ολόκληρος ο χώρος των διατάξεων να μπορεί να χαρακτηριστεί από μια κατανομή πιθανοτήτων Boltzmann. Ο Geoffrey Hinton και οι συνεργάτες του ανέπτυξαν έναν τρόπο εκπαίδευσης της μηχανής Boltzmann ως γενετικού μοντέλου: Όταν της παρουσιάζονταν ως εισροές διάφορα στοιχεία που είχαν όλα ένα κοινό χαρακτηριστικό, παρήγαγε περισσότερα στοιχεία του ίδιου τύπου. (Σχήμα από τον Freddie Pagani.)
Το βασικό συστατικό για την εύρεση αυτού του είδους κοινών στοιχείων ήταν η επαύξηση του δικτύου, ώστε να περιλαμβάνει περισσότερους κόμβους από αυτούς που κωδικοποιούν τα δεδομένα. Αυτοί οι κρυφοί κόμβοι, που απεικονίζονται με γκρι χρώμα στην Εικ.2, επιτρέπουν στο σύστημα να καταγράφει συσχετίσεις υψηλότερου επιπέδου μεταξύ των δεδομένων.
Κατ’ αρχήν, η μηχανή Boltzmann θα μπορούσε να χρησιμοποιηθεί για τη μηχανική αναγνώριση ενός χειρόγραφου ή για τη διάκριση μεταξύ κανονικών και έκτακτων συνθηκών σε μια εγκατάσταση όπως ένας σταθμός παραγωγής ενέργειας. Δυστυχώς, ο αλγόριθμος μάθησης της μηχανής Boltzmann είναι απαγορευτικά αργός για τις περισσότερες πρακτικές εφαρμογές. Παρέμεινε θέμα ακαδημαϊκής έρευνας, αλλά δεν βρήκε μεγάλη χρήση στον πραγματικό κόσμο –μέχρι που έκανε μια εκπληκτική επανεμφάνιση αρκετά χρόνια αργότερα.
ΠΩΣ ΔΟΥΛΕΥΟΥΝ ΤΑ ΔΙΚΤΥΑ
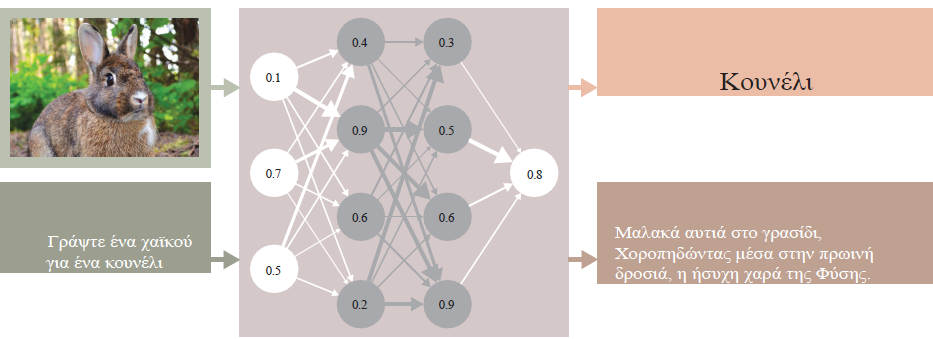
Περίπου την ίδια εποχή, ο Hinton εργαζόταν με τον γνωστικό επιστήμονα David Rumelhart πάνω σε έναν άλλο αλγόριθμο μάθησης, ο οποίος θα γινόταν το μυστικό της επιτυχίας σχεδόν όλων των σημερινών νευρωνικών δικτύων: οπισθοδιάδοση (backpropagation).[6] Ο αλγόριθμος αναπτύχθηκε για ένα διαφορετικό είδος αρχιτεκτονικής δικτύου, που ονομάζεται δίκτυο πρόσθιας τροφοδότησης (feedforward network), όπως φαίνεται στην Εικ.3. Σε αντίθεση με το δίκτυο Hopfield και τη μηχανή Boltzmann, με τις αμφίδρομες συνδέσεις μεταξύ των κόμβων, τα σήματα σε ένα δίκτυο πρόσθιας τροφοδότησης ρέουν προς μία μόνο κατεύθυνση: από ένα επίπεδο νευρώνων εισόδου, μέσω κάποιου αριθμού κρυφών επιπέδων, στην έξοδο. Μια παρόμοια αρχιτεκτονική είχε χρησιμοποιηθεί στο πολυεπίπεδο perceptron.
Ας υποθέσουμε ότι θέλετε να εκπαιδεύσετε ένα δίκτυο πρόσθιας τροφοδότησης για την ταξινόμηση εικόνων. Του δίνετε μια εικόνα ενός κουνελιού και θέλετε να παράγει το μήνυμα εξόδου «Αυτό είναι ένα κουνέλι». Αλλά κάτι δεν πάει καλά και αντ’ αυτού λαμβάνετε το μήνυμα εξόδου «Αυτό είναι χελώνα». Πώς μπορείτε να επαναφέρετε τα πράγματα στη σωστή πορεία; Το δίκτυο μπορεί να έχει δεκάδες ή εκατοντάδες –ή σήμερα, τρισεκατομμύρια– συνδέσεις μεταξύ κόμβων που συμβάλλουν στην έξοδο, η καθεμία με το δικό της αριθμητικό βάρος. Συνεπώς ο αριθμός των τρόπων που υπάρχουν για να τους ρυθμίσετε όλους, ώστε να προσπαθήσετε να πάρετε την έξοδο που θέλετε, είναι ασύλληπτος.
Η οπισθοδιάδοση λύνει αυτό το πρόβλημα μέσω του αλγόριθμου καθοδικής πορείας κατά μήκος της κλίσης (gradient descent): Πρώτα, ορίζετε μια συνάρτηση σφάλματος που προσδιορίζει πόσο απέχει η έξοδος που πήρατε από την έξοδο που θέλετε. Στη συνέχεια, υπολογίζετε τις μερικές παραγώγους της συνάρτησης σφάλματος με κριτήριο κάθε ένα από τα ενδοκομβικά βάρη –ένα απλό θέμα επανειλημμένης εφαρμογής του αλυσιδωτού κανόνα του λογισμού. Τέλος, χρησιμοποιείτε αυτές τις παραγώγους για να προσαρμόσετε τα βάρη με τρόπο που να μειώνει το σφάλμα.
Εικ. 3. Ένα δίκτυο πρόσθιας τροφοδότησης, εκπαιδευμένο με οπισθοδιάδοση, είναι η βασική δομή των νευρωνικών δικτύων που χρησιμοποιούνται σήμερα. Περνώντας αριθμητικά σήματα από ένα επίπεδο εισόδου μέσω κρυφών επιπέδων σε ένα επίπεδο εξόδου, τα δίκτυα πρόσθιας τροφοδότησης εκτελούν λειτουργίες που περιλαμβάνουν την ταξινόμηση εικόνων και την παραγωγή κειμένου. (Εικόνα από τον Freddie Pagani· φωτογραφία κουνελιού από τον JM Ligero Loarte/Wikimedia Commons/CC BY 3.0· χαϊκού[i] που δημιουργήθηκε από τον GPT-4, OpenAI, 22 Οκτωβρίου 2024).
Μπορεί να χρειαστούν πολλές επαναλήψεις για να περιοριστεί το σφάλμα αρκετά κοντά στο μηδέν –και θα θέλετε να βεβαιωθείτε ότι το δίκτυο δίνει το σωστό αποτέλεσμα για πολλά εισερχόμενα δεδομένα, όχι μόνο για ένα. Αλλά αυτά τα βασικά βήματα χρησιμοποιούνται για την εκπαίδευση όλων των ειδών των δικτύων, συμπεριλαμβανομένων των ταξινομητών εικόνων βάσει επαλήθευσης-της-γενικής-ιδέας και των μεγάλων γλωσσικών μοντέλων, όπως το ChatGPT.
Η μέθοδος του αλγόριθμου καθοδικής πορείας κατά μήκος της κλίσης είναι διαισθητικά κομψή και δεν ήταν καινούρια εννοιολογικά. «Αλλά έπρεπε να συγκεντρωθούν πολλά στοιχεία για να λειτουργήσει η ιδέα της οπισθοδιάδοσης», λέει ο McClelland. «Δεν μπορείτε να πάρετε την παράγωγο κάποιου πράγματος αν αυτό δεν είναι παραγωγίσιμο». Οι πραγματικοί νευρώνες λειτουργούν λίγο-πολύ σε διακριτές καταστάσεις ενεργοποίησης και απενεργοποίησης, και το αρχικό δίκτυο Hopfield, η μηχανή Boltzmann και το perceptron ήταν όλα διακριτά μοντέλα. Για να λειτουργήσει η οπισθοδιάδοση, ήταν απαραίτητο να μεταβούμε σε ένα μοντέλο στο οποίο οι καταστάσεις των κόμβων μπορούν να πάρουν ένα συνεχές φάσμα τιμών. Αλλά αυτά τα δίκτυα συνεχών τιμών είχαν ήδη εισαχθεί, μεταξύ άλλων σε μια εργασία του Hopfield το 1984.[7]
Μια δεύτερη καινοτομία έπρεπε να περιμένει για καιρό. Η οπισθοδιάδοση λειτούργησε καλά για δίκτυα με μερικά μόνο επίπεδα. Αλλά όταν ο αριθμός των επιπέδων πλησίαζε τα πέντε ή και περισσότερα –ένας ασήμαντος αριθμός για τα δεδομένα της εποχής– ορισμένες από τις επιμέρους παραγώγους ήταν τόσο μικρές που η εκπαίδευση διαρκούσε πολύ ώστε πρακτικά να ήταν ανέφικτη.
Στις αρχές της δεκαετίας του 2000, ο Hinton βρήκε μια λύση, η οποία περιλάμβανε την παλιά του μηχανή Boltzmann –ή μάλλον μια λεγόμενη περιορισμένη εκδοχή της, στην οποία οι μόνες συνδέσεις είναι αυτές μεταξύ ενός κρυμμένου νευρώνα και ενός ορατού (μη κρυμμένου) νευρώνα.[8] Οι περιορισμένες μηχανές Boltzmann (Restricted Boltzmann Machines, RBM) είναι εύκολο να μοντελοποιηθούν υπολογιστικά, επειδή κάθε ομάδα νευρώνων –ορατών και κρυφών– θα μπορούσε να επικαιροποιηθεί ταυτόχρονα και τα αριθμητικά βάρη σύνδεσης θα μπορούσαν να ρυθμιστούν όλα μαζί σε ένα μόνο βήμα. Η ιδέα του Hinton ήταν να απομονώσει ζεύγη διαδοχικών επιπέδων σε ένα δίκτυο πρόσθιας τροφοδότησης, να τα εκπαιδεύσει σαν να επρόκειτο για RBM για να προσεγγίσει τα αριθμητικά βάρη και, στη συνέχεια, να συντονίσει το σύνολο του δικτύου χρησιμοποιώντας οπισθοδιάδοση.
«Ήταν κάπως άκομψο, αλλά δούλεψε και ο κόσμος ενθουσιάστηκε», λέει ο Graham Taylor, του Πανεπιστημίου του Guelph στον Καναδά, ο οποίος πήρε το διδακτορικό του υπό την επίβλεψη του Hinton το 2009. «Ήταν πλέον δυνατό να εκπαιδεύσουμε δίκτυα με πέντε, έξι, επτά επίπεδα. Οι άνθρωποι τα αποκαλούσαν «βαθιά» δίκτυα και άρχισαν να χρησιμοποιούν τον όρο βαθεία μάθηση (deep learning).
Το τέχνασμα με τις RBM δεν χρησιμοποιήθηκε για πολύ. Η υπολογιστική ισχύς εξελισσόταν τόσο γρήγορα –ιδιαίτερα με τη συνειδητοποίηση ότι οι μονάδες επεξεργασίας γραφικών (GPU) ήταν ιδανικά κατάλληλες για τους υπολογισμούς που απαιτούνταν για τα νευρωνικά δίκτυα– ώστε μέσα σε λίγα χρόνια, ήταν δυνατό να επιτευχθεί οπισθοδιάδοση σε ακόμη μεγαλύτερα δίκτυα από την αρχή, χωρίς να απαιτούνται RBM.
«Αν η μάθηση μέσω RBM δεν είχε συμβεί, θα είχαν εμφανιστεί οι GPU ούτως ή άλλως;» αναρωτιέται ο Taylor. «Αυτό είναι συζητήσιμο. Αλλά ο ενθουσιασμός γύρω από τις RBM άλλαξε το τοπίο: οδήγησε στην επιστράτευση και εκπαίδευση νέων φοιτητών και σε νέους τρόπους σκέψης. Νομίζω πως, τουλάχιστον, δεν θα είχε συμβεί με τον ίδιο τρόπο».
O, ΤΙ ΕΙΝΑΙ ΚΑΙΝΟΥΡΙΟ ΕΙΝΑΙ ΠΑΛΙΟ
Τα σημερινά δίκτυα χρησιμοποιούν εκατοντάδες ή χιλιάδες επίπεδα, αλλά η μορφή τους είναι ελάχιστα διαφορετική από εκείνη που περιέγραψε ο Hinton. «Έμαθα για τα νευρωνικά δίκτυα από βιβλία της δεκαετίας του 1980», λέει ο Bernhard Mehlig, του Πανεπιστημίου του Γκέτεμποργκ στη Σουηδία. «Όταν άρχισα να τα διδάσκω, συνειδητοποίησα ότι τα περισσότερα δεν είναι καινούργια. Είναι, επί της ουσίας, παλιά πράγματα». Ο Mehlig σημειώνει ότι σε ένα εγχειρίδιο που έγραψε, το οποίο εκδόθηκε το 2021, το πρώτο από τα τρία μέρη αφορά στον Hopfield και το δεύτερο στον Hinton.
Τα νευρωνικά δίκτυα επηρεάζουν πλέον έναν τεράστιο αριθμό ανθρώπινων προσπαθειών, εμπλέκονται στην ανάλυση δεδομένων, στις αναζητήσεις στο διαδίκτυο και στη δημιουργία γραφικών. Είναι ευφυή; Είναι εύκολο να απορρίψει κανείς το ερώτημα αυτό χωρίς πολύ σκέψη. «Πάντα υπήρχαν πολλά πράγματα που οι μηχανές μπορούσαν να κάνουν καλύτερα από τους ανθρώπους», λέει ο Sankar Das Sarma του Πανεπιστημίου του Μέριλαντ. «Αυτό δεν έχει καμία σχέση με το να γίνουνε άνθρωποι. Το ChatGPT είναι εντυπωσιακά καλό σε ορισμένα πράγματα, αλλά σε πολλά άλλα δεν πλησιάζει καν ένα μωρό δύο ετών».
Μια ενδεικτική σύγκριση είναι το τεράστιο χάσμα δεδομένων μεταξύ των σημερινών νευρωνικών δικτύων και των ανθρώπων.[9] Ένας εγγράμματος 20 ετών μπορεί να έχει διαβάσει και ακούσει μερικές εκατοντάδες εκατομμύρια λέξεις στη ζωή του μέχρι τώρα. Αντίθετα, τα μεγάλα γλωσσικά μοντέλα εκπαιδεύονται σε εκατοντάδες δισεκατομμύρια λέξεις, αριθμός που αυξάνεται με κάθε νέα έκδοση. Όταν συνυπολογίσετε το γεγονός ότι το ChatGPT έχει το πλεονέκτημα μιας εμπειρίας ζωής χίλιες φορές μεγαλύτερης από εσάς, οι ικανότητές του μπορεί να φαίνονται λιγότερο σαν νοημοσύνη. Ίσως όμως να μην έχει σημασία αν η τεχνητή νοημοσύνη αποτυγχάνει σε κάποιες εργασίες, αν είναι καλή στον σωστό συνδυασμό άλλων.
Οι Hinton και Hopfield έχουν και οι δύο αναφερθεί στους κινδύνους της ανεξέλεγκτης τεχνητής νοημοσύνης. Ανάμεσα στα επιχειρήματά τους είναι η ιδέα ότι μόλις οι μηχανές γίνουν ικανές να αναλύουν τους στόχους σε επιμέρους στόχους, θα συμπεράνουν γρήγορα ότι μπορούν να κάνουν σχεδόν κάθε εργασία ευκολότερη για τον εαυτό τους, εδραιώνοντας τη δική τους δύναμη. Και επειδή τα νευρωνικά δίκτυα είναι συχνά επιφορτισμένα με τη συγγραφή κώδικα για άλλους υπολογιστές, το να σταματήσει η ζημιά δεν είναι τόσο απλό όσο το να τραβήξει κανείς την πρίζα από μια μεμονωμένη μηχανή.
«Υπάρχουν επίσης άμεσοι κίνδυνοι που αντιμετωπίζουμε αυτή τη στιγμή», λέει ο Mehlig. «Υπάρχουν κείμενα γραμμένα από υπολογιστή και ψεύτικες εικόνες που χρησιμοποιούνται για να ξεγελάσουν τους ανθρώπους και να επηρεάσουν τις εκλογές. Νομίζω ότι μιλώντας για την κατάκτηση του κόσμου από τους υπολογιστές, οι άνθρωποι παίρνουν λιγότερο σοβαρά τους άμεσους κινδύνους».
ΤΙ ΜΠΟΡΟΥΝ ΝΑ ΚΑΝΟΥΝ ΟΙ ΦΥΣΙΚΟΙ;
Μεγάλο μέρος της ανησυχίας προέρχεται από το γεγονός ότι είναι πολύ λίγα γνωστά για το τι πραγματικά κάνουν τα νευρωνικά δίκτυα: Πώς μέσα από δισεκατομμύρια πολλαπλασιασμούς πινάκων καταλήγουμε να είμαστε σε θέση να βρίσκουμε πρωτεϊνικές δομές ή να γράφουμε ποίηση; «Οι άνθρωποι στις μεγάλες εταιρείες ενδιαφέρονται περισσότερο για την παραγωγή εσόδων, παρά για την κατανόηση», λέει ο Das Sarma. «Η κατανόηση απαιτεί περισσότερο χρόνο. Η δουλειά των θεωρητικών είναι να κατανοούν τα φαινόμενα, και αυτό είναι ένα τεράστιο φυσικό φαινόμενο που εκκρεμεί να κατανοηθεί από εμάς. Οι φυσικοί πρέπει να ενδιαφέρονται γι’ αυτό».
«Είναι δύσκολο να μην είσαι ενθουσιασμένος με αυτό που συμβαίνει και είναι δύσκολο να μην
παρατηρήσουμε πως δεν καταλαβαίνουμε», λέει ο Bialek. «Αν θέλετε να πείτε ότι τα πράγματα είναι αναδυόμενα, ποια είναι η παράμετρος τάξης και τι είναι αυτό που έχει αναδυθεί; Η φυσική έχει έναν τρόπο να κάνει αυτό το ερώτημα πιο συγκεκριμένο. Θα αποφέρει αυτή η προσέγγιση γνώση; Θα το δούμε».
Προς το παρόν, τα μεγαλύτερα ερωτήματα εξακολουθούν να είναι κατακλυσμιαία. «Αν υπήρχε κάτι προφανές που θα ερχόταν στο μυαλό μας, θα υπήρχε μια ορδή ανθρώπων που θα προσπαθούσαν να το λύσουν», λέει ο Hopfield. «Αλλά κάτι τέτοιο δεν συμβαίνει επειδή κανείς δεν ξέρει από πού να ξεκινήσει».
Ωστόσο, μερικά ερωτήματα μικρότερης κλίμακας είναι πιο εύκολα αντιμετωπίσιμα. Για παράδειγμα, γιατί η οπισθοδιάδοση μειώνει το σφάλμα του δικτύου κοντά στο μηδέν με τέτοια αξιοπιστία, αντί να «κολλάει» σε υψηλά τοπικά ελάχιστα, όπως κάνει το δίκτυο Hopefield; «Υπήρξε μια πολύ καλή εργασία πάνω σε αυτό πριν από μερικά χρόνια από τον Surya Ganguli στο Στάνφορντ», λέει η Sara Solla του Πανεπιστημίου Nortwestern. «Διαπίστωσε ότι τα περισσότερα υψηλά ελάχιστα είναι στην πραγματικότητα σαγματικά σημεία[10]: Είναι ένα ελάχιστο σε πολλές διαστάσεις, αλλά υπάρχει πάντα μία στην οποία δεν είναι. Έτσι, αν συνεχίσετε να προσπαθείτε, τελικά θα βρείτε τη διέξοδο».
Όταν οι ερευνητές με εκπαίδευση φυσικού εργάζονται σε τέτοια προβλήματα, εξακολουθούν να ασχολούνται με τη φυσική; Ή έχουν αφήσει τη φυσική πίσω τους για κάτι άλλο; Αν η «φυσική» ορίζεται ως η μελέτη του φυσικού, υλικού κόσμου, αυτό αναμφισβήτητα θα απέκλειε τα τεχνητά νευρωνικά δίκτυα, τα οποία μέχρι τώρα είναι εξ ολοκλήρου αφηρημένες, ανθρώπινες κατασκευές με ελάχιστη ομοιότητα με τους βιολογικούς νευρώνες. «Δεν φτιάχνουμε αεροπλάνα που κουνάνε τα φτερά τους», λέει η Solla. «Και η οπισθοδιάδοση είναι ένας εντελώς μη ρεαλιστικός μηχανισμός σε έναν πραγματικό εγκέφαλο. Ο κατασκευαστικός στόχος είναι να φτιάξουμε μια μηχανή που να λειτουργεί. Η φύση μας δίνει κάποια εικόνα, αλλά η καλύτερη λύση δεν είναι απαραίτητα να την αντιγράψουμε».
Πρέπει, όμως, η φυσική να ορίζεται αποκλειστικά από το αντικείμενό της; «Στα διεπιστημονικά πεδία, αυτό που κάνει τη διαφορά μεταξύ των επιστημονικών κλάδων –μαθηματικών, πληροφορικής και φυσικής– είναι οι μέθοδοι και οι νοοτροπίες τους», λέει η Francesca Mignacco από το Πρίνστον. «Είναι συμπληρωματικές, αλλά διαφορετικές. Τα μοντέλα των νευρωνικών δικτύων είναι τόσο πολύπλοκα που είναι δύσκολο να επιτευχθούν αυστηρές μαθηματικές περιγραφές. Αλλά η στατιστική φυσική διαθέτει ακριβώς τα εργαλεία για να αντιμετωπίσει την πολυπλοκότητα των συστημάτων υψηλής διάστασης. Προσωπικά, ποτέ δεν σταμάτησα να θέτω ερωτήματα μόνο και μόνο επειδή μπορεί να είναι ή να μην είναι φυσική».
«Η φυσική περιορίζεται μόνο από την επινοητικότητα των ανθρώπων που εφαρμόζουν μεθόδους της φυσικής σε συστήματα στον πραγματικό κόσμο», λέει ο Hopfield. «Μπορείτε να είστε προκατειλημμένοι με αυτό ή μπορείτε να υποδεχθείτε την εφαρμοσμένη φυσική. Εγώ είμαι ένας από τους φιλόξενους».
ΕΥΧΑΡΙΣΤΙΕΣ
Reproduced from Nobel Prize highlights neural networks’ physics roots. The road to the modern machine-learning marvels was paved with ideas from statistical mechanics and collective phenomena. Physics Today 77 (12), 12–16 (2024); (https://doi.org/10.1063/pt.qjmx.snxw) with the permission of the American Institute of Physics.
ΣΗΜΕΙΩΣΕΙΣ
[1] Μετάφραση του ρητού στην αγγλική «Garbage in, garbage out» [ΣτΕ].
[2] Τηλεπαιχνίδι γνώσεων [ΣτΜ].
[3] Hopfield, J., J., 1982. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 79, 2554, 1982. https://www.pnas.org/doi/pdf/10.1073/pnas.79.8.2554
[4] Fahlman, S., Ε., Hinton, G., E., and Sejnowski, T. J., 1983. Massively Parallel Architectures for Al: NETL, Thistle, and Boltzmann Machines, in Proceedings of the AAAI Conference on Artificial Intelligence, 3, Association for the Advancement of Artificial Intelligence, 1983, p. 109. https://aaai.org/papers/00109-aaai83-087-massively-parallel-architectures-for-al-netl-thistle-and-boltzmann-machines/
[5] Ackley, D., H., Hinton, G., E., Sejnowski, T., J., 1985. A learning algorithm for Boltzmann machines. Cogn. Sci. 9, 147. https://www.sciencedirect.com/science/article/pii/S0364021385800124
[6] Rumelhart, D., E., Hinton, G., E., and Williams, R. J., 1986. Learning representations by back-propagating errors. Nature 323, 533. https://www.nature.com/articles/323533a0
[7] Hopfield, J., J., 1984. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 81, 3088. https://www.pnas.org/doi/10.1073/pnas.81.10.3088
[8] Hinton, G., E., 2002. Training Products of Experts by Minimizing Contrastive Divergence. Neural Comput. 14, 1771. https://direct.mit.edu/neco/article-abstract/14/8/1771/6687/Training-Products-of-Experts-by-Minimizing?redirectedFrom=fulltext; Hinton, G., E., Osindero, S., Teh, Y.,-W., 2006. A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527. https://pubmed.ncbi.nlm.nih.gov/16764513/
[9] Frank, M., C., 2023. Bridging the data gap between children and large language models. Trends Cogn. Sci. 27, 990. https://www.sciencedirect.com/science/article/abs/pii/S1364661323002036
[10] Κρίσιμα σημεία στην επιφάνεια της γραφικής παράστασης μιας συνάρτησης, όπου οι μερικές παράγωγοι προς όλες τις κατευθύνσεις έχουν την τιμή μηδέν, τα οποία δεν είναι τοπικά ακρότατα (μέγιστα ή ελάχιστα) [ΣτΜ].
[i] Ιαπωνική ποιητική φόρμα [ΣτΕ].