Διάλεξη Νόμπελ, 12 Δεκεμβρίου, 1933
Μετάφραση: Βαρβάρα Πετανίδου
Επιμέλεια Μετάφρασης: Κέλη Σπυροπούλου, Βασίλης Λεμπέσης
«…για την ανακάλυψη νέων παραγωγικών μορφών της ατομικής θεωρίας». (Από την προσφώνηση στην τελετή απονομής του βραβείου Nobel, 11 Δεκεμβρίου 1933)
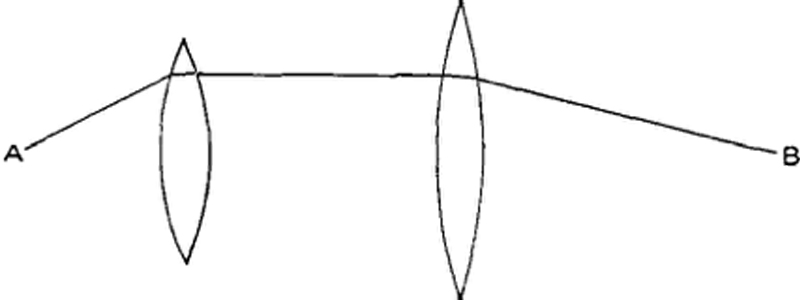
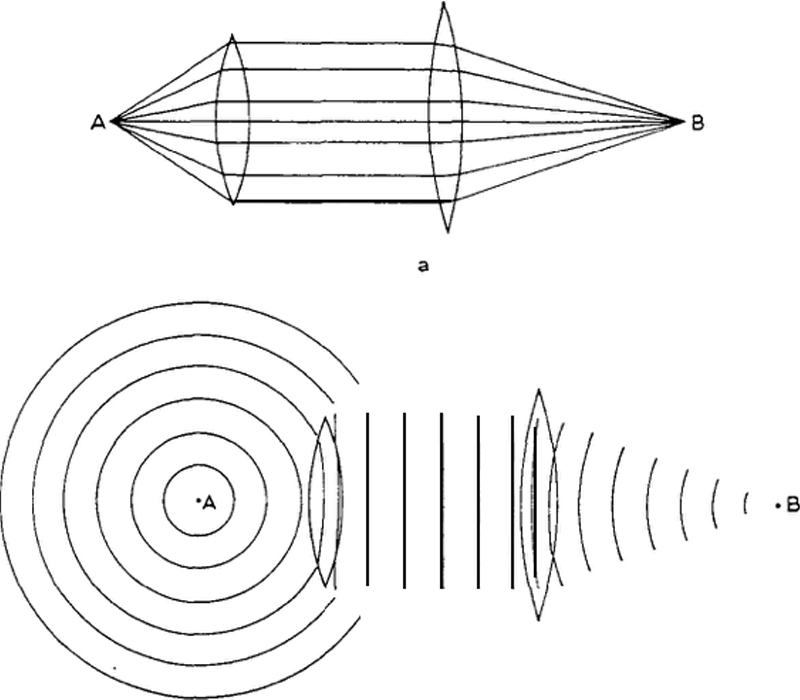
Κατά τη διαδρομή μιας ακτίνας φωτός μέσα από ένα οπτικό όργανο, όπως ένα τηλεσκόπιο ή έναν φακό φωτογραφικής μηχανής, αυτή υφίσταται αλλαγή κατεύθυνσης σε κάθε διαθλαστική ή ανακλαστική επιφάνεια. Η πορεία των ακτίνων μπορεί να ανακατασκευαστεί, αν γνωρίζουμε τους δύο απλούς νόμους που διέπουν τις αλλαγές στην κατεύθυνση: τον νόμο της διάθλασης που ανακαλύφθηκε από τον Snellius πριν από μερικές εκατοντάδες χρόνια και τον νόμο της ανάκλασης, με τον οποίο ο Αρχιμήδης ήταν εξοικειωμένος πάνω από 2.000 χρόνια πριν. Ως απλό παράδειγμα, το Σχ. 1 δείχνει μια ακτίνα Α-Β, η οποία υπόκειται σε διάθλαση σε καθεμία από τις τέσσερις συνοριακές επιφάνειες δύο φακών σύμφωνα με τον νόμο του Snellius.
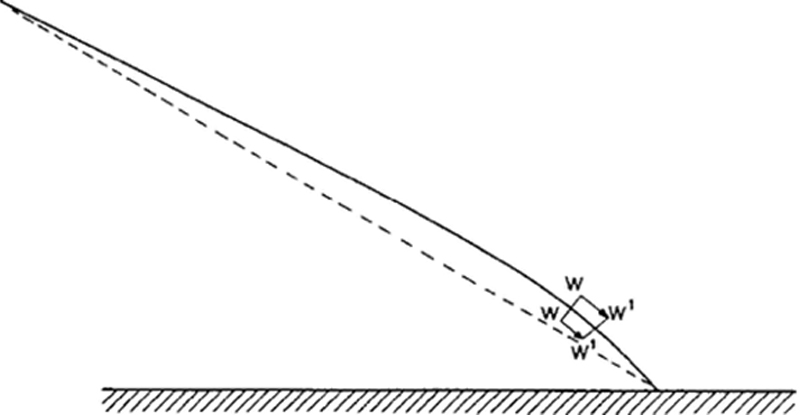
Ο Φερμά (Fermat) όρισε τη συνολική διαδρομή μιας ακτίνας φωτός από μια πιο γενική άποψη. Σε διαφορετικά μέσα το φως διαδίδεται με διαφορετικές ταχύτητες και η διαδρομή της ακτινοβολίας δίνει την εντύπωση ότι το φως πρέπει να φτάσει στον προορισμό του όσο το δυνατόν γρηγορότερα. Παρεμπιπτόντως, εδώ επιτρέπεται να θεωρήσουμε δύο οποιαδήποτε σημεία κατά μήκος της ακτίνας ως σημεία εκκίνησης και τερματισμού. Η ελάχιστη απόκλιση από τη διαδρομή που ακολουθείται πραγματικά θα σήμαινε καθυστέρηση. Αυτή είναι η περίφημη αρχή του ελαχίστου χρόνου για το φως του Φερμά, η οποία με θαυμαστό τρόπο καθορίζει την τύχη μιας ακτίνας φωτός με μια μόνο δήλωση και περιλαμβάνει επίσης τη γενικότερη περίπτωση, όταν η φύση του μέσου μεταβάλλεται όχι απότομα όπως σε μεμονωμένες επιφάνειες αλλά σταδιακά από σημείο σε σημείο. Η ατμόσφαιρα της γης παρέχει ένα παράδειγμα. Όσο πιο βαθιά διεισδύει σε αυτήν μια ακτίνα φωτός από το διάστημα, τόσο πιο αργά προχωρά μέσα σε έναν όλο και πιο πυκνό αέρα. Παρόλο που οι διαφορές στην ταχύτητα διάδοσης είναι απειροελάχιστες, η αρχή του Φερμά υπό αυτές τις συνθήκες απαιτεί η ακτίνα φωτός να καμπυλώνει προς τη γη (βλ. Σχ. 2), έτσι ώστε να παραμείνει λίγο περισσότερο στα υψηλότερα «ταχύτερα» στρώματα και να φτάσει στον προορισμό της πιο γρήγορα σε σχέση με τη συντομότερη ευθεία διαδρομή (διακεκομμένη γραμμή στο σχήμα- αγνοήστε το τετράγωνο, WWW1W1 προς το παρόν).
Νομίζω ότι σχεδόν κανένας από εσάς δε θα έχει παραλείψει να παρατηρήσει ότι ο ήλιος όταν είναι χαμηλά στον ορίζοντα δε φαίνεται να είναι κυκλικός αλλά πεπλατυσμένος: η κατακόρυφη διάμετρός του φαίνεται να είναι μειωμένη. Αυτό είναι ένα αποτέλεσμα της καμπυλότητας των ακτίνων.
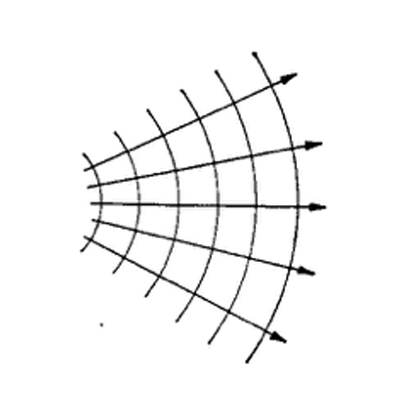
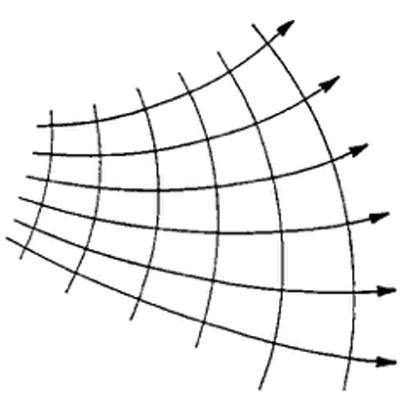
Σύμφωνα με την κυματική θεωρία, οι ακτίνες του φωτός, αυστηρά μιλώντας, έχουν μόνο πλασματική σημασία. Δεν είναι οι φυσικές τροχιές κάποιων σωματιδίων του φωτός αλλά μια μαθηματική κατασκευή, οι λεγόμενες ορθογώνιες τροχιές των κυματικών επιφανειών, φανταστικές γραμμές-οδηγοί κατά κάποιον τρόπο, οι οποίες δείχνουν προς την κατεύθυνση που είναι κάθετη προς την κυματική επιφάνεια στην οποία η τελευταία προχωρά (βλ. το Σχ. 3 που δείχνει την απλούστερη περίπτωση ομόκεντρων σφαιρικών κυματικών επιφανειών και αντίστοιχα ευθύγραμμων ακτίνων, ενώ το Σχ. 4 απεικονίζει την περίπτωση των καμπύλων ακτίνων).
Είναι εκπληκτικό το γεγονός ότι μια γενική αρχή τόσο σημαντική όσο αυτή του Φερμά σχετίζεται άμεσα με αυτές τις μαθηματικές κατευθυντήριες γραμμές και όχι με τις κυματικές επιφάνειες, και για τον λόγο αυτό θα μπορούσε κανείς να τη θεωρήσει ως ένα απλό μαθηματικό αξιοπερίεργο. Κάθε άλλο. Γίνεται ορθώς κατανοητή μόνο από τη σκοπιά της κυματικής θεωρίας και παύει να είναι ένα θεϊκό θαύμα. Από την άποψη των κυμάτων, η λεγόμενη καμπυλότητα της φωτεινής ακτίνας είναι πιο εύκολα κατανοητή ως μια εκτροπή της κυματικής επιφάνειας, η οποία πρέπει προφανώς να συμβαίνει όταν γειτονικά τμήματα μιας κυματικής επιφάνειας προχωρούν με διαφορετικές ταχύτητες- με τον ίδιο ακριβώς τρόπο που ένα άγημα στρατιωτών βαδίζοντας προς τα εμπρός θα εκτελέσει τη διαταγή «κλίνατ’ επί δεξιά» κάνοντας βήματα διαφορετικού μήκους, ο άντρας της δεξιάς πτέρυγας το μικρότερο και ο άντρας της αριστερής πτέρυγας το μεγαλύτερο. Στην ατμοσφαιρική διάθλαση της ακτινοβολίας για παράδειγμα (Σχ. 2), το τμήμα της κυματικής επιφάνειας WW πρέπει αναγκαστικά να στραφεί προς τα δεξιά προς το W1W1, επειδή το αριστερό του μισό βρίσκεται σε ελαφρώς υψηλότερο, μικρότερης πυκνότητας αέρα, και έτσι προχωράει ταχύτερα από το δεξιό τμήμα που βρίσκεται σε χαμηλότερο σημείο. Παρεμπιπτόντως, θα ήθελα να αναφερθώ σε ένα σημείο στο οποίο η αρχή του Snellius αποτυγχάνει: μια οριζόντια εκπεμπόμενη φωτεινή ακτίνα θα πρέπει να παραμένει οριζόντια, επειδή, ο δείκτης διάθλασης δε μεταβάλλεται στην οριζόντια κατεύθυνση. Στην πραγματικότητα, μια οριζόντια ακτίνα καμπυλώνεται πιο έντονα από οποιαδήποτε άλλη, πράγμα που αποτελεί προφανή συνέπεια της θεωρίας του εκτρεπόμενου μετώπου κύματος. Κατά τη λεπτομερή εξέταση της αρχής του Φερμά διαπιστώνεται ότι ισοδυναμεί πλήρως με την τετριμμένη και προφανή δήλωση ότι – δεδομένης της τοπικής κατανομής των ταχυτήτων του φωτός – το μέτωπο του κύματος πρέπει να εκτρέπεται με τον τρόπο που υποδεικνύεται. Δεν μπορώ να το αποδείξω αυτό εδώ, αλλά θα προσπαθήσω να δώσω μια εύλογη εξήγηση. Θα σας ζητούσα και πάλι να φανταστείτε μια σειρά στρατιωτών που βαδίζουν προς τα εμπρός. Για να εξασφαλιστεί ότι η γραμμή παραμένει αδιάσπαστη, οι άνδρες συνδέονται με μια μακριά ράβδο που ο καθένας κρατάει σταθερά στο χέρι του. Δε δίνεται καμία εντολή ως προς την κατεύθυνση- η μόνη εντολή είναι: ο κάθε άνδρας να βαδίζει ή να τρέχει όσο πιο γρήγορα μπορεί. Εάν η φύση του εδάφους ποικίλλει αργά από τόπο σε τόπο, θα είναι πότε η δεξιά πτέρυγα πότε η αριστερή που θα προχωρήσει πιο γρήγορα, και οι αλλαγές στην κατεύθυνση θα συμβούν αυθόρμητα. Αφού περάσει κάποιο χρονικό διάστημα, θα φανεί ότι ολόκληρη η διαδρομή που διανύεται δεν είναι ευθύγραμμη αλλά, κατά κάποιο τρόπο, καμπυλωτή. Ότι αυτή η καμπυλωτή διαδρομή είναι ακριβώς εκείνη με την οποία ο προορισμός που θα μπορούσε να επιτευχθεί ανά πάσα στιγμή μπορεί να επιτευχθεί ταχύτερα ανάλογα με τη φύση του εδάφους είναι τουλάχιστον αρκετά εύλογο, δεδομένου ότι ο καθένας από τους άνδρες έκανε ό,τι καλύτερο μπορούσε. Θα φανεί ακόμα ότι η εκτροπή συμβαίνει επίσης σταθερά προς εκείνη την κατεύθυνση στην οποία το έδαφος είναι λιγότερο ομαλό, έτσι ώστε να καταλήξει στο τέλος να φαίνεται ότι οι άνδρες είχαν σκόπιμα “παρακάμψει” ένα μέρος όπου θα προχωρούσαν αργά.
Η αρχή του Φερμά φαίνεται έτσι να είναι η τετριμμένη πεμπτουσία της κυματικής θεωρίας. Ήταν λοιπόν μια αξιομνημόνευτη περίσταση όταν ο Χάμιλτον (Hamilton) έκανε την ανακάλυψη ότι η πραγματική κίνηση σημειακών μαζών σε ένα πεδίο δυνάμεων (π.χ. ενός πλανήτη στην τροχιά του γύρω από τον ήλιο ή μιας πέτρας που ρίχνεται στο βαρυτικό πεδίο της γης) διέπεται επίσης από μια παρόμοια γενική αρχή, η οποία φέρει, και έχει κάνει έκτοτε διάσημο, το όνομα του εμπνευστή της. Ομολογουμένως, η αρχή Χάμιλτον δε λέει ακριβώς ότι η σημειακή μάζα επιλέγει τον ταχύτερο δρόμο, αλλά λέει κάτι τόσο παρόμοιο: η αναλογία με την αρχή του συντομότερου χρόνου που ταξιδεύει το φως είναι τόσο κοντινή, ώστε να βρεθεί κανείς μπροστά σε έναν γρίφο. Φαινόταν σαν η Φύση να είχε υπαγορεύσει τον ίδιο νόμο δύο φορές σε εντελώς διαφορετικά μέσα: πρώτα στην περίπτωση του φωτός, μέσω ενός αρκετά προφανούς παίγνιου των ακτίνων, κι έπειτα στην περίπτωση των σημειακών μαζών, που κάθε άλλο παρά προφανείς ήταν, εκτός αν έπρεπε να αποδοθεί και σ’ αυτά με κάποιον τρόπο κυματική φύση. Και αυτό φαινόταν αδύνατο να γίνει. Διότι οι «σημειακές μάζες», στις οποίες οι νόμοι της μηχανικής είχαν πράγματι επιβεβαιωθεί πειραματικά εκείνη την εποχή, ήταν μόνο τα μεγάλα, ορατά, μερικές φορές πολύ μεγάλα σώματα, οι πλανήτες, για τα οποία κάτι σαν την «κυματική φύση» φαινόταν να αποκλείεται.
Τα μικρότερα, στοιχειώδη συστατικά της ύλης, τα οποία σήμερα, πιο συγκεκριμένα, αποκαλούμε «σημειακές μάζες», ήταν τότε καθαρά υποθετικά. Μόνο μετά την ανακάλυψη της ραδιενέργειας οι συνεχείς βελτιώσεις των μεθόδων μέτρησης επέτρεψαν τη λεπτομερή μελέτη των ιδιοτήτων αυτών των σωματιδίων και επιτρέπουν σήμερα τη φωτογράφιση των διαδρομών αυτών των σωματιδίων και την ακριβή μέτρησή τους (στερεοφωτογραμμετρικά) με τη λαμπρή μέθοδο του C. T. R. Wilson1. Όσον αφορά τις μετρήσεις, επιβεβαιώνουν ότι για τα σωματίδια ισχύουν οι ίδιοι νόμοι της μηχανικής όπως και για τα μεγάλα σώματα, τους πλανήτες κ.λπ. Ωστόσο, διαπιστώθηκε ότι ούτε το μόριο ούτε το μεμονωμένο άτομο μπορούν να θεωρηθούν ως το «απόλυτο συστατικό»: αλλά ότι ακόμη και το άτομο είναι ένα σύστημα με εξαιρετικά πολύπλοκη δομή. Στο μυαλό μας σχηματίζονται εικόνες της δομής των ατόμων που αποτελούνται από σωματίδια, οι οποίες φαίνεται να έχουν κάποια ομοιότητα με το πλανητικό σύστημα. Ήταν φυσικό, αρχικά, να γίνει η προσπάθεια ώστε να θεωρηθούν έγκυροι οι ίδιοι νόμοι της κίνησης που είχαν αποδειχθεί ότι ικανοποιούνταν σε μεγάλη κλίμακα. Με άλλα λόγια, η μηχανική του Χάμιλτον, η οποία, όπως είπα παραπάνω, κορυφώνεται με την αρχή Χάμιλτον, εφαρμόστηκε και στην «εσωτερική ζωή» του ατόμου. Το ότι υπάρχει μια πολύ στενή αναλογία μεταξύ της αρχής του Χάμιλτον και της αρχής του Φερμά είχε εν τω μεταξύ σχεδόν ξεχαστεί. Στην περίπτωση που το θυμόντουσαν, θεωρούνταν ότι δεν ήταν τίποτε περισσότερο από ένα περίεργο χαρακτηριστικό της μαθηματικής θεωρίας.
Τώρα είναι πολύ δύσκολο, χωρίς να υπεισέλθουμε περαιτέρω σε λεπτομέρειες, να αποδώσουμε σωστά την αντίληψη της επιτυχίας ή της αποτυχίας αυτών των κλασικών-μηχανικών εικόνων του ατόμου. Από τη μια πλευρά, η αρχή του Χάμιλτον, ειδικότερα, αποδείχθηκε ο πιο πιστός και αξιόπιστος οδηγός, ο οποίος ήταν απλώς απαραίτητος- από την άλλη πλευρά έπρεπε να υποστεί κανείς, για να αποδώσει δικαιοσύνη στα γεγονότα, την πρόχειρη παρεμβολή εντελώς νέων ακατανόητων αξιωμάτων, των λεγόμενων κβαντικών συνθηκών και κβαντικών αξιωμάτων. Σαν μια έντονη δυσαρμονία στη συμφωνία της κλασικής μηχανικής – που όμως είναι παράξενα οικεία – παιγμένη σαν να ήταν στο ίδιο όργανο. Με μαθηματικούς όρους μπορούμε να το διατυπώσουμε ως εξής: ενώ η αρχή του Χάμιλτον απλώς αξιώνει ότι ένα δεδομένο ολοκλήρωμα πρέπει να είναι ελάχιστο, χωρίς η αριθμητική τιμή του ελαχίστου να καθορίζεται από αυτό το αξίωμα, τώρα απαιτείται η αριθμητική τιμή του ελαχίστου να περιορίζεται σε ακέραια πολλαπλάσια μιας παγκόσμιας φυσικής σταθεράς, του κβάντου δράσης του Πλανκ. Αυτό συμπτωματικά. Η κατάσταση ήταν αρκετά απελπιστική. Αν η παλιά μηχανική είχε αποτύχει εντελώς, δε θα ήταν τόσο άσχημα. Τότε ο δρόμος θα ήταν ελεύθερος για την ανάπτυξη ενός νέου συστήματος μηχανικής. Όπως και να ‘ταν, βρισκόταν κανείς αντιμέτωπος με το δύσκολο έργο να σώσει την ψυχή του παλιού συστήματος, του οποίου το πνεύμα σαφώς κυριαρχούσε σ’ αυτόν τον μικρόκοσμο, και ταυτόχρονα να το κολακεύσει, ώστε να δεχτεί τις κβαντικές συνθήκες όχι ως μεγάλη παρεμβολή αλλά ως προερχόμενες από την ίδια του την εσώτερη ουσία.
Η διέξοδος βρισκόταν ακριβώς στη δυνατότητα που ήδη αναφέρθηκε παραπάνω, να αποδοθεί στην αρχή Χάμιλτον η λειτουργία ενός κυματικού μηχανισμού στον οποίο βασίζονται ουσιαστικά οι σημειακές μηχανικές διαδικασίες, όπως ακριβώς είχε συνηθίσει κανείς να κάνει στην περίπτωση των φαινομένων που σχετίζονται με το φως και την αρχή Φερμά που τα διέπει. Ομολογουμένως, η μεμονωμένη διαδρομή μιας σημειακής μάζας χάνει την ορθή φυσική της σημασία και γίνεται τόσο πλασματική όσο και η διακριτή απομονωμένη ακτίνα φωτός. Η ουσία της θεωρίας η ελάχιστη αρχή, ωστόσο, όχι μόνο παραμένει ανέπαφη, αλλά αποκαλύπτει το αληθινό και απλό νόημά της μόνο υπό την κυματοειδή διάσταση, όπως έχει ήδη εξηγηθεί. Αυστηρά μιλώντας, η νέα θεωρία δεν είναι στην πραγματικότητα νέα, είναι μια εντελώς οργανική εξέλιξη, ώστε θα μπορούσε σχεδόν να μπει κανείς στον πειρασμό να πει μια πιο περίτεχνη εκδοχή της παλιάς θεωρίας.
Πώς λοιπόν αυτή η νέα, πιο «περίτεχνη» εκδοχή οδήγησε σε αξιοσημείωτα διαφορετικά αποτελέσματα; Τι της επέτρεψε, όταν εφαρμόστηκε στο άτομο, να αποφύγει δυσκολίες που η παλιά θεωρία δεν μπορούσε να λύσει; Τι της επέτρεψε να καταστήσει αποδεκτές τις μεγάλες παρεμβάσεις ή ακόμη και να τις οικειοποιηθεί;
Και πάλι, τα θέματα αυτά μπορούν να διευκρινιστούν καλύτερα αξιοποιώντας την αναλογία με την οπτική. Πολύ σωστά, πράγματι, αποκάλεσα προηγουμένως την αρχή του Φερμά ως την πεμπτουσία της κυματικής θεωρίας του φωτός, ωστόσο, δεν μπορεί να καταστήσει αναπόφευκτη μια πιο ακριβή μελέτη της ίδιας της κυματικής διαδικασίας. Τα λεγόμενα φαινόμενα διάθλασης και συμβολής του φωτός μπορούν να γίνουν κατανοητά μόνο αν παρακολουθήσουμε λεπτομερώς την κυματική διαδικασία, διότι αυτό που έχει σημασία δεν είναι μόνο ο τελικός προορισμός του κύματος, αλλά και το αν σε μια δεδομένη στιγμή καταφτάνει εκεί με μια κορυφή ή με μια κοιλάδα του. Στις παλαιότερες, πιο χονδροειδείς πειραματικές διατάξεις, τα φαινόμενα αυτά λάμβαναν χώρα μόνο ως μικρές λεπτομέρειες και διέφευγαν της παρατήρησης. Μόλις έγιναν αντιληπτά και ερμηνεύτηκαν σωστά μέσω των κυμάτων, ήταν εύκολο να επινοηθούν πειράματα, στα οποία η κυματική φύση του φωτός εμφανίζεται όχι μόνο σε μικρές λεπτομέρειες αλλά σε πολύ μεγάλη κλίμακα σε ολόκληρη την έκταση του φαινομένου.
Επιτρέψτε μου να το διευκρινίσω αυτό με δύο παραδείγματα: πρώτον, το παράδειγμα ενός οπτικού οργάνου, όπως το τηλεσκόπιο, το μικροσκόπιο κ.λπ. Ο στόχος εδώ είναι να επιτευχθεί μια ευκρινής εικόνα, δηλαδή είναι επιθυμητό όλες οι ακτίνες που ξεκινούν από ένα σημείο να επανενωθούν σε ένα σημείο, τη λεγόμενη εστία (βλ. Σχ. 5α). Αρχικά θεωρήθηκε ότι μόνο οι γεωμετρικές-οπτικές δυσκολίες εμπόδιζαν την επίτευξη αυτού του στόχου. αυτές είναι πράγματι σημαντικές.
Αργότερα διαπιστώθηκε ότι ακόμη και στα καλύτερα σχεδιασμένα όργανα η εστίαση των ακτίνων ήταν σημαντικά υποδεέστερη από ό,τι θα αναμενόταν, αν κάθε ακτίνα υπάκουε ακριβώς στην αρχή του Φερμά ανεξάρτητα από τις γειτονικές ακτίνες. Το φως που εξέρχεται από ένα σημείο και συλλαμβάνεται από το όργανο ξανασμίγει πίσω από το όργανο όχι πλέον σε ένα μόνο σημείο, αλλά κατανεμημένο σε μια μικρή κυκλική περιοχή, τον λεγόμενο δίσκο περίθλασης, ο οποίος, κατά τα άλλα, είναι στις περισσότερες περιπτώσεις κυκλικός μόνο και μόνο επειδή τα ανοίγματα και τα περιγράμματα των φακών είναι γενικά κυκλικά. Διότι, η αιτία του φαινομένου που ονομάζουμε περίθλαση έγκειται στο ότι δεν μπορεί το όργανο να συμπεριλάβει όλα τα σφαιρικά κύματα που προέρχονται από το σημείο του αντικειμένου. Τα άκρα του φακού και τα τυχόν ανοίγματα απλώς αποκόπτουν ένα μέρος των κυματικών επιφανειών (βλ. Σχ. 5β) και – αν μου επιτρέπετε να χρησιμοποιήσω μια πιο υπαινικτική έκφραση – τα τραχέα περιθώρια αντιστέκονται στην πλήρη επανένωση των ακτίνων σε ένα σημείο και παράγουν την κάπως θολή ή ασαφή εικόνα. Ο βαθμός ασάφειας συνδέεται στενά με το μήκος κύματος του φωτός και είναι απολύτως αναπόφευκτος λόγω αυτής της βαθιά ριζωμένης θεωρητικής σχέσης. Δύσκολα αντιληπτή στην αρχή, διέπει και περιορίζει την απόδοση του σύγχρονου μικροσκοπίου, το οποίο έχει υπερβεί όλα τα άλλα σφάλματα αναπαραγωγής μιας εικόνας. Οι εικόνες που λαμβάνονται από δομές όχι πολύ πιο μεγάλες ή και ακόμη πιο μικρές σε μέγεθος από τα μήκη κύματος του φωτός μοιάζουν μόνο εξ αποστάσεως ή καθόλου με το πρωτότυπο.
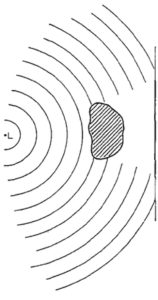
Ένα δεύτερο, ακόμη πιο απλό παράδειγμα είναι η σκιά ενός αδιαφανούς αντικειμένου που πέφτει πάνω σε μια οθόνη από μια μικρή σημειακή πηγή φωτός. Για να κατασκευαστεί η μορφή της σκιάς, πρέπει να ανιχνευθεί κάθε ακτίνα φωτός και να διαπιστωθεί αν το αδιαφανές αντικείμενο την εμποδίζει να φτάσει στην οθόνη. Το περίγραμμα της σκιάς σχηματίζεται από τις ακτίνες φωτός που μόλις περνούν από την άκρη του σώματος. Η εμπειρία έχει δείξει ότι το περίγραμμα της σκιάς δεν είναι απολύτως ευκρινές ακόμη και με μια σημειακή πηγή φωτός και ένα ευκρινές αντικείμενο που ρίχνει σκιά. Ο λόγος γι’ αυτό είναι ο ίδιος όπως και στο πρώτο παράδειγμα. Το μέτωπο του κύματος διχοτομείται κατά κάποιον τρόπο από το σώμα (βλ. Σχ. 6) και τα ίχνη αυτής της αλλοίωσης έχουν ως αποτέλεσμα τη θόλωση του περιγράμματος της σκιάς, η οποία θα ήταν ακατανόητη, εάν οι επιμέρους ακτίνες φωτός ήταν ανεξάρτητες οντότητες που προχωρούσαν ανεξάρτητα η μία από την άλλη χωρίς αναφορά στις γειτονικές τους.
Το φαινόμενο αυτό – που ονομάζεται επίσης περίθλαση – δεν είναι κατά κανόνα αισθητό σε μεγάλα σώματα. Αν όμως το σώμα που ρίχνει τη σκιά είναι πολύ μικρό, τουλάχιστον στη μία διάσταση, η περίθλαση εκφράζεται πρώτον με το ότι δε σχηματίζεται καθόλου σωστή σκιά και δεύτερον -πολύ πιο εντυπωσιακά- με το ότι το ίδιο το μικρό σώμα είναι σαν να ήταν το ίδιο μια πηγή φωτός και εκπέμπει φως προς όλες τις κατευθύνσεις. (κατά προτίμηση βέβαια σε μικρές γωνίες σε σχέση με το προσπίπτον φως).
Όλοι σας είστε αναμφίβολα εξοικειωμένοι με τους λεγόμενους «κόκκους σκόνης» σε μια δέσμη φωτός που πέφτει σε ένα σκοτεινό δωμάτιο. Τα λεπτά χορταράκια και οι ιστοί αράχνης στην κορυφή ενός λόφου με τον ήλιο πίσω τους ή οι ακατάστατες μπούκλες μαλλιών ενός ανθρώπου που στέκεται με τον ήλιο πίσω του και συχνά φωτίζονται μυστηριωδώς από το περιθλώμενο φως καθώς και η ορατότητα του καπνού και της ομίχλης βασίζονται σε αυτό το φαινόμενο . Δεν προέρχεται στην πραγματικότητα από το ίδιο το σώμα αλλά από το άμεσο περιβάλλον του, μια περιοχή στην οποία η παρουσία του σώματος προκαλεί σημαντική συμβολή στα προσπίπτοντα μέτωπα των κυμάτων. Είναι ενδιαφέρον και σημαντικό για ό,τι ακολουθεί να παρατηρήσουμε ότι η περιοχή της συμβολής έχει πάντα και προς κάθε κατεύθυνση τουλάχιστον την έκταση ενός ή μερικών μηκών κύματος, όσο μικρό κι αν είναι το διαταράσσον σωματίδιο. Για άλλη μια φορά, λοιπόν, παρατηρούμε μια στενή σχέση μεταξύ του φαινομένου της περίθλασης και του μήκους κύματος. Αυτό αναδεικνύεται ίσως καλύτερα με αναφορά σε μια άλλη κυματική διαδικασία, στον ήχο. Λόγω του πολύ μεγαλύτερου μήκους κύματος, το οποίο είναι της τάξης των εκατοστών και των μέτρων, ο σχηματισμός σκιών υποχωρεί στην περίπτωση του ήχου και η περίθλαση παίζει πρακτικά σημαντικό ρόλο: μπορούμε εύκολα να ακούσουμε έναν άνθρωπο να φωνάζει πίσω από έναν ψηλό τοίχο ή πίσω από τη γωνία ενός συμπαγούς σπιτιού, ακόμη και αν δεν τον βλέπουμε.
Ας επιστρέψουμε από την οπτική στη μηχανική και ας εξερευνήσουμε την αναλογία στο μέγιστο βαθμό. Στην οπτική, το παλιό σύστημα της μηχανικής αντιστοιχεί σε μια νοητική εργασία με απομονωμένες αμοιβαία ανεξάρτητες ακτίνες φωτός. Η νέα κυματική μηχανική αντιστοιχεί στην κυματική θεωρία του φωτός. Αυτό που αποκομίζεται περνώντας από την παλαιά άποψη στη νέα είναι ότι τα φαινόμενα περίθλασης μπορούν να συμπεριληφθούν ή, για να το εκφράσουμε καλύτερα, αυτό που αποκομίζεται είναι κάτι αυστηρά ανάλογο με τα φαινόμενα περίθλασης του φωτός, και το οποίο στο σύνολό του πρέπει να είναι πολύ ασήμαντο, διαφορετικά η παλαιά άποψη της μηχανικής δε θα ήταν επαρκής τόσον καιρό. Είναι, ωστόσο, εύκολο να υποθέσουμε ότι το φαινόμενο που αγνοήσαμε μπορεί σε ορισμένες περιπτώσεις να γίνει πολύ αισθητό, οπότε θα επιβληθεί πλήρως στη μηχανική διαδικασία και το παλιό σύστημα θα έλθει αντιμέτωπο με άλυτους γρίφους, αν ολόκληρο το μηχανικό σύστημα είναι συγκρίσιμο σε μέγεθος με τα μήκη κύματος των “κυμάτων της ύλης” που παίζουν τον ίδιο ρόλο στις μηχανικές διαδικασίες με αυτόν που παίζουν τα κύματα του φωτός στις οπτικές διαδικασίες.
Αυτός είναι ο λόγος για τον οποίο σε αυτά τα μικροσκοπικά συστήματα, τα άτομα, ήταν βέβαιο ότι θα αποτύγχανε η παλαιά άποψη, η οποία, παρόλο που παρέμενε ακλόνητη ως μια καλή προσέγγιση για τις γενικές μηχανικές διεργασίες, δεν είναι πλέον επαρκής για τις ευαίσθητες αλληλεπιδράσεις σε περιοχές της τάξης μεγέθους ενός ή μερικών μηκών κύματος. Ήταν εκπληκτικό να παρατηρεί κανείς τον τρόπο με τον οποίο όλες αυτές οι παράξενες πρόσθετες απαιτήσεις αναπτύχθηκαν αυθόρμητα από τη νέα κυματική θεώρηση, ενώ έπρεπε να επιβληθούν στην παλιά θεώρηση, για να προσαρμοστούν στην εσωτερική ζωή του ατόμου και να δώσουν κάποια εξήγηση στα παρατηρούμενα γεγονότα.
Έτσι, το σημαντικότερο σημείο του όλου θέματος είναι ότι οι διάμετροι των ατόμων και το μήκος κύματος των υποθετικών υλικών κυμάτων είναι περίπου της ίδιας τάξης μεγέθους. Και τώρα θα πρέπει οπωσδήποτε να ρωτήσετε αν πρέπει να θεωρηθεί απλή τύχη το γεγονός ότι στη συνεχή ανάλυσή μας για τη δομή της ύλης θα καταλήξουμε από όλα τα σημεία στην τάξη μεγέθους του μήκους κύματος ή αν αυτό είναι σε κάποιο βαθμό κατανοητό. Περαιτέρω, μπορεί να ρωτήσετε πώς γνωρίζουμε ότι αυτό είναι έτσι, αφού τα υλικά κύματα αποτελούν μια εντελώς νέα απαίτηση αυτής της θεωρίας, άγνωστη οπουδήποτε αλλού. Ή μήπως απλώς πρόκειται για μια υπόθεση που έπρεπε να γίνει;
Η συμφωνία μεταξύ των τάξεων μεγέθους δεν είναι απλά τυχαία ούτε απαιτείται κάποια ειδική υπόθεση σχετικά με αυτήν. προκύπτει αυτόματα από τη θεωρία με τον ακόλουθο αξιοσημείωτο τρόπο. Το γεγονός ότι ο βαρύς πυρήνας του ατόμου είναι πολύ μικρότερος από το άτομο και επομένως μπορεί να θεωρηθεί ως ένα σημειακό κέντρο έλξης στο επιχείρημα που ακολουθεί, όπως τεκμηριώνεται πειραματικά από τα πειράματα για τη σκέδαση των ακτίνων άλφα που έκαναν οι Rutherford και Chadwick. Αντί των ηλεκτρονίων εισάγουμε υποθετικά κύματα, των οποίων τα μήκη κύματος αφήνονται εντελώς ελεύθερα, επειδή δε γνωρίζουμε ακόμη τίποτα γι’ αυτά. Αυτό αφήνει μια σταθερά, π.χ. α, που υποδηλώνει ένα άγνωστο ακόμη μέγεθος στον υπολογισμό μας. Ωστόσο, το έχουμε συνηθίσει αυτό σε τέτοιους υπολογισμούς και δε μας εμποδίζει να υπολογίσουμε ότι ο πυρήνας του ατόμου πρέπει να παράγει ένα είδος φαινομένου περίθλασης σε αυτά τα κύματα, παρόμοια όπως κάνει ένα μικροσκοπικό σωματίδιο σκόνης στα κύματα του φωτός. Κατ’ αναλογία, προκύπτει ότι υπάρχει στενή σχέση μεταξύ της έκτασης της περιοχής συμβολής με την οποία περιβάλλεται ο πυρήνας και του μήκους κύματος, και ότι τα δύο είναι της ίδιας τάξης μεγέθους. Για το τι είναι αυτό έπρεπε να το αφήσουμε ανοιχτό- αλλά το πιο σημαντικό βήμα ακολουθεί τώρα: ταυτίζουμε την περιοχή συμβολής, το φωτοστέφανο περίθλασης, με το άτομο. ισχυριζόμαστε ότι το άτομο στην πραγματικότητα είναι απλώς το αποτέλεσμα της περίθλασης ενός κύματος ηλεκτρονίων που συλλαμβάνεται, όπως λέγαμε, από τον πυρήνα του ατόμου. Δεν είναι πλέον θέμα τύχης το γεγονός ότι το μέγεθος του ατόμου και το μήκος κύματος είναι της ίδιας τάξης μεγέθους. είναι θέμα φύσης. Δε γνωρίζουμε την αριθμητική τιμή κανενός από τα δύο, γιατί έχουμε ακόμη στον υπολογισμό μας τη μία άγνωστη σταθερά, την οποία ονομάσαμε α. Υπάρχουν δύο πιθανοί τρόποι προσδιορισμού της, οι οποίοι παρέχουν αμοιβαίο έλεγχο ο ένας στον άλλον. Πρώτον, μπορούμε να την επιλέξουμε έτσι ώστε οι εκδηλώσεις της ζωής του ατόμου, κυρίως οι γραμμές του φάσματος που εκπέμπονται, να βγαίνουν σωστά ποσοτικά- αυτές άλλωστε μπορούν να μετρηθούν με μεγάλη ακρίβεια. Δεύτερον, μπορούμε να επιλέξουμε τη σταθερά α με τέτοιον τρόπο, ώστε το φωτοστέφανο περίθλασης να αποκτήσει το μέγεθος που απαιτείται για το άτομο. Αυτοί οι δύο προσδιορισμοί του α (εκ των οποίων ο δεύτερος είναι ομολογουμένως πολύ πιο ασαφής, επειδή το «μέγεθος του ατόμου» δεν είναι σαφώς καθορισμένος όρος) βρίσκονται σε πλήρη συμφωνία μεταξύ τους. Τρίτον, και τελευταίο, μπορούμε να παρατηρήσουμε ότι η σταθερά που παραμένει άγνωστη, από φυσική άποψη, δεν έχει στην πραγματικότητα τη διάσταση ενός μήκους, αλλά μιας δράσης, δηλαδή ενέργειας πολλαπλασιασμένης με τον χρόνο. Ένα προφανές βήμα, λοιπόν, είναι να την αντικαταστήσουμε με την αριθμητική τιμή του παγκόσμιου κβάντου δράσης του Planck, η οποία είναι γνωστή με ακρίβεια από τους νόμους της θερμικής ακτινοβολίας. Θα δούμε ότι επιστρέφουμε με την πλήρη, σημαντική πλέον, ακρίβεια στον πρώτο (ακριβέστερο) τρόπο προσδιορισμού.
Ποσοτικά μιλώντας, η θεωρία επομένως τα καταφέρνει με ελάχιστες νέες παραδοχές. Περιέχει μια και μόνη διαθέσιμη σταθερά, στην οποία πρέπει να δοθεί μια αριθμητική τιμή γνωστή από την παλαιότερη κβαντική θεωρία, πρώτον για να αποδοθεί στα φωτεινά αποτυπώματα της περίθλασης το σωστό μέγεθος, ώστε να μπορούν να ταυτιστούν λογικά με τα άτομα, και δεύτερον για να εκτιμηθούν ποσοτικά και σωστά όλες οι εκδηλώσεις της ζωής του ατόμου, το φως που εκπέμπει, η ενέργεια ιονισμού κ.λπ.
Προσπάθησα να σας παρουσιάσω τη θεμελιώδη ιδέα της κυματικής θεωρίας της ύλης στην απλούστερη δυνατή μορφή. Πρέπει να παραδεχτώ τώρα ότι στην επιθυμία μου να μην μπλέξω τις ιδέες από την αρχή, έκανα περιττές προσθήκες. Όχι όσον αφορά τον υψηλό βαθμό στον οποίο όλα τα επαρκώς προσεκτικά εξαγόμενα συμπεράσματα επιβεβαιώνονται από την εμπειρία, αλλά όσον αφορά την εννοιολογική ευκολία και απλότητα με την οποία καταλήγουμε στα συμπεράσματα. Δε μιλάω εδώ για τις μαθηματικές δυσκολίες, οι οποίες αποδεικνύονται πάντα ασήμαντες στο τέλος, αλλά για τις εννοιολογικές δυσκολίες. Είναι, βέβαια, εύκολο να πούμε ότι στρεφόμαστε από την έννοια της καμπύλης διαδρομής σε ένα σύστημα κυματικών επιφανειών κάθετων σε αυτήν. Οι κυματικές επιφάνειες, ωστόσο, ακόμη και αν εξετάσουμε μόνο μικρά τμήματά τους (βλ. Σχ. 7), περιλαμβάνουν τουλάχιστον μια στενή δέσμη πιθανών καμπύλων διαδρομών,
με όλες να υπακούουν στην ίδια σχέση. Σύμφωνα με την παλαιότερη άποψη, αλλά όχι σύμφωνα με τη νέα, μία από αυτές σε κάθε συγκεκριμένη μεμονωμένη περίπτωση διακρίνεται από όλες τις άλλες που είναι «μόνο δυνατές» ως αυτή που «πραγματικά ταξίδεψε». Βρισκόμαστε εδώ αντιμέτωποι με την πλήρη ισχύ της λογικής αντίθεσης μεταξύ του
είτε – ή (μηχανική του σημείου)
και του
τόσο – όσο (κυματική μηχανική).
Αυτό δε θα είχε μεγάλη σημασία, αν το παλιό σύστημα εγκαταλείπονταν εντελώς και αντικαθίστατο από το νέο. Δυστυχώς, αυτό δε συμβαίνει. Από την άποψη της κυματικής μηχανικής, η άπειρη σειρά πιθανών σημειακών διαδρομών θα ήταν απλώς πλασματική, καμία από αυτές δε θα είχε το προνόμιο έναντι των άλλων να είναι αυτή που πραγματικά ταξιδεύει σε μια μεμονωμένη περίπτωση. Έχω, ωστόσο, ήδη αναφέρει ότι έχουμε παρατηρήσει, σε ορισμένες περιπτώσεις, ατομικές διαδρομές σωματιδίων στην πραγματικότητα. Η κυματική θεωρία μπορεί να το αναπαραστήσει αυτό είτε καθόλου είτε μόνο πολύ ατελώς. Μας είναι τρομερά δύσκολο να ερμηνεύσουμε τα ίχνη που βλέπουμε ως τίποτα περισσότερο από στενές δέσμες εξίσου πιθανών διαδρομών, μεταξύ των οποίων οι κυματικές επιφάνειες δημιουργούν διασταυρούμενες συνδέσεις. Ωστόσο, αυτές οι διασταυρούμενες συνδέσεις είναι απαραίτητες για την κατανόηση των φαινομένων περίθλασης και συμβολής, τα οποία μπορούν να αποδειχθούν για το ίδιο σωματίδιο με την ίδια αληθοφάνεια – και μάλιστα σε μεγάλη κλίμακα, όχι μόνο ως συνέπεια των θεωρητικών ιδεών για το εσωτερικό του ατόμου, τις οποίες αναφέραμε προηγουμένως. Οι συνθήκες είναι ομολογουμένως τέτοιες, ώστε να μπορούμε πάντα να τα καταφέρνουμε σε κάθε μεμονωμένη περίπτωση χωρίς οι δύο διαφορετικές εκδοχές να οδηγούν σε διαφορετικές προσδοκίες όσον αφορά το αποτέλεσμα ορισμένων πειραμάτων. Δεν μπορούμε, ωστόσο, να τα καταφέρουμε με τέτοιους παλιούς, οικείους και φαινομενικά απαραίτητους όρους όπως «πραγματικό» ή «μόνο δυνατό». Ποτέ δεν είμαστε σε θέση να πούμε τι πραγματικά είναι ή τι πραγματικά συμβαίνει, αλλά μπορούμε μόνο να πούμε τι θα παρατηρηθεί σε κάθε συγκεκριμένη περίπτωση. Θα πρέπει να είμαστε μόνιμα ικανοποιημένοι με αυτό… ; Εν πρώτοις, ναι. Κατ’ αρχήν, δεν υπάρχει τίποτα καινούργιο στο αξίωμα ότι τελικά η ακριβής επιστήμη δεν πρέπει να στοχεύει σε τίποτε περισσότερο από την περιγραφή αυτού που μπορεί πραγματικά να παρατηρηθεί. Το ερώτημα είναι μόνο αν από εδώ και στο εξής θα πρέπει να απέχουμε από το να συνδέουμε την περιγραφή με μια σαφή υπόθεση για την πραγματική φύση του κόσμου. Υπάρχουν πολλοί που επιθυμούν να κηρύξουν μια τέτοια παραίτηση ακόμη και σήμερα. Πιστεύω όμως ότι αυτό σημαίνει να κάνουμε τα πράγματα υπερβολικά εύκολα για τον εαυτό μας.
Θα όριζα την παρούσα κατάσταση των γνώσεών μας ως εξής. Η μεν ακτίνα ή η διαδρομή του σωματιδίου αντιστοιχεί σε μια διαμήκη σχέση της διαδικασίας διάδοσης (δηλαδή στη διεύθυνση διάδοσης), η δε κυματική επιφάνεια σε μια εγκάρσια σχέση (δηλαδή ορθογώνια προς αυτήν). Και οι δύο σχέσεις είναι αναμφίβολα πραγματικές. η μία αποδεικνύεται από διαδρομές σωματιδίων που έχουν φωτογραφηθεί, η άλλη από πειράματα συμβολής. Ο συνδυασμός και των δύο σε ένα ομοιόμορφο σύστημα έχει αποδειχθεί αδύνατος µέχρι σήµερα. Μόνο σε ακραίες περιπτώσεις επικρατεί σε τέτοιο βαθμό είτε η εγκάρσια κυψελοειδής είτε η ακτινική, διαμήκης σχέση, ώστε νομίζουμε ότι μπορούμε να αρκεστούμε μόνο στην κυματική θεωρία ή μόνο στη σωματιδιακή θεωρία.
Ο Erwin Schrödinger (12 Αυγούστου 1887 – 4 Ιανουαρίου 1961) ήταν Αυστριακός θεωρητικός φυσικός, ένας από τους πρωτοπόρους της κβαντικής θεωρίας. Η σημαντικότερη συνεισφορά του ήταν η διατύπωση της ομώνυμης εξίσωσης η οποία περιγράφει την χρονική εξέλιξη της κυματοσυνάρτησης ενός κβαντικού συστήματος. Ήταν αυτός που εισήγαγε τον όρο της κβαντικής σύμπλεξης (quantum entanglement), το 1932, και ο πρώτος που επιχείρησε μια συζήτηση των συνέπειών της.
ΕΥΧΑΡΙΣΤΙΕΣ
Το πορτραίτο του Schrödinger φιλοτέχνησε ο εικαστικός Χρήστος Αλαβέρας από τη Θεσσαλονίκη.
ΥΠΟΣΗΜΕΙΩΣΕΙΣ
- Το 1910, ο Wilson συνέλαβε την ιδέα ότι θα μπορούσε να απεικονίσει τα ίχνη των φορτισμένων σωματιδίων φωτογραφίζοντας τα ρεύματα των σταγονιδίων νερού που συμπυκνώνονται σε ιόντα που δημιουργήθηκαν καθώς τα σωματίδια περνούσαν μέσα από τον θάλαμο. Η ευαισθησία ήταν τέτοια που ένα μόνο φορτισμένο σωματίδιο μπορούσε να λειτουργήσει ως κέντρο συμπύκνωσης. Ο Wilson τιμήθηκε με το Νόμπελ Φυσικής το 1927 για αυτήν την εφεύρεση.