
Απεικόνιση ατόμων παγιδευμένων σε οπτικό πλέγμα. Ευγενική προσφορά στο InS του I. Bloch, καθηγητή στο Πανεπιστήμιο Ludwig Maximilian (LMU) του Μονάχου και Διευθυντή Ερευνών στο Ινστιτούτο Κβαντικής Οπτικής Max Planck στο Garching της Γερμανίας.
Σε αυτό το άρθρο θα αναφερθούμε στην πιο θεαματική, ίσως, εφαρμογή της παγίδευσης της ατομικής κίνησης: τους οπτικούς κρυστάλλους. Πρόκειται για φυσικά συστήματα στα οποία παγιδεύονται άτομα μέσα σε οπτικά πλέγματα, δηλαδή σε οπτικά πεδία που η έντασή τους εμφανίζει περιοδικότητα, σε μία, δύο και τρεις διαστάσεις και θυμίζουν τη μορφή των κρυσταλλικών πλεγμάτων των στερεών σωμάτων. Η σημασία των οπτικών κρυστάλλων ατόμων πάει πολύ πιο πέρα από μια απλή ομοιότητα μορφής και γεωμετρίας με τους κρυστάλλους των στερεών σωμάτων καθώς ανοίγουν, στην κυριολεξία, νέους ορίζοντες στην ατομική φυσική και στη φυσική της συμπυκνωμένης ύλης.
Η ΚΑΤΑΣΚΕΥΗ ΕΝΟΣ ΟΠΤΙΚΟΥ ΠΛΕΓΜΑΤΟΣ
Η κατασκευή ενός οπτικού πλέγματος είναι εξαιρετικά απλή. Το μόνο που χρειάζεται είναι δύο όμοιες (σε πλάτος, συχνότητα και πόλωση) δέσμες λέιζερ που διαδίδονται σε αντίθετη κατεύθυνση και συμβάλλουν μεταξύ τους. Με αυτό τον τρόπο προκύπτει ένα στάσιμο ηλεκτρομαγνητικό κύμα του οποίου η ένταση εμφανίζει περιοδικότητα σε μια διάσταση (στην διεύθυνση της διάδοσης των δύο δεσμών), όπως φαίνεται στην Εικ. 1. Με ανάλογο τρόπο, αν οδηγήσουμε σε συμβολή ζεύγη δεσμών κατά μήκος των άλλων δύο διαστάσεων του χώρου, μπορούμε να κατασκευάσουμε ηλεκτρομαγνητικά πεδία με περιοδικότητα στις δύο ή και στις τρεις διαστάσεις όπως φαίνεται και στην Εικ. 2 (Bloch, 2005).
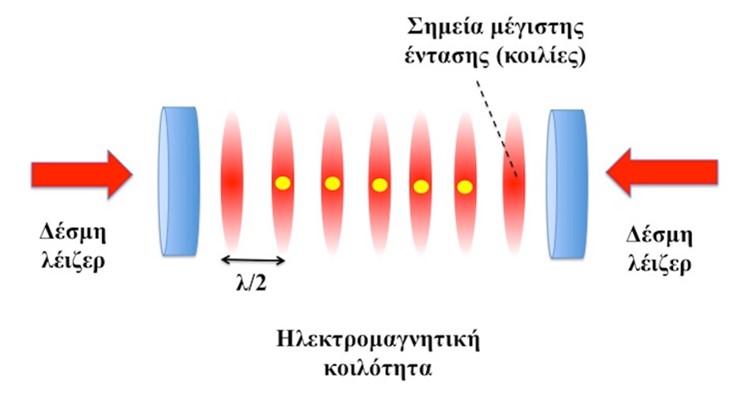
Εικόνα 1. Το στάσιμο ηλεκτρομαγνητικό κύμα προκύπτει από τη συμβολή δύο αντίθετα διαδιδόμενων δεσμών λέιζερ. Τα σημεία μέγιστης (ελάχιστης) έντασης απέχουν μεταξύ τους απόσταση ίση με το μισό του μήκους κυμάτων λ των δύο δεσμών λέιζερ. Στα σημεία αυτά μπορούν να παγιδευτούν άτομα (κίτρινοι δίσκοι)
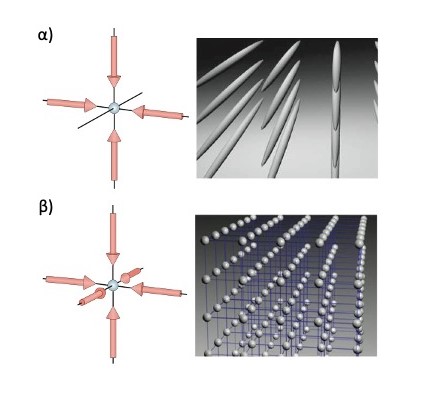
Εικόνα 2. a) Οπτικά πλέγματα σε δύο διαστάσεις. Τα άτομα παγιδεύονται σε περιοχές με κυλινδρική γεωμετρία. β) Οπτικά πλέγματα σε τρεις διαστάσεις. Τα άτομα παγιδεύονται γύρω από συγκεκριμένα σημεία του χώρου.
Όταν ένα άτομο, που έχει προηγουμένως επιβραδυνθεί, βρεθεί μέσα σε ένα οπτικό πλέγμα υπόκειται σε ένα οπτικό διπολικό δυναμικό και παγιδεύεται στα σημεία που η τιμή της έντασης του φωτός είναι μέγιστη ή μηδενική. Το άτομο βρίσκεται στην ουσία παγιδευμένο από ένα δυναμικό που έχει τη χωρική περιοδικότητα της έντασης του πεδίου. Μια καλλιτεχνική αναπαράσταση του δυναμικού αυτού και των παγιδευμένων ατόμων δίνεται στην Εικ.3. Όπως, εύστοχα, έχει σχολιάσει ο φυσικός Ι. Deutsch, τα παγιδευμένα άτομα στα οπτικά πλέγματα μοιάζουν με αυγά τοποθετημένα σε καρτέλες. Τα πειράματα με οπτικά πλέγματα άρχισαν στις αρχές της δεκαετίας του ’90 με πρωτοπόρες τις ερευνητικές ομάδες του G. Grynberg στην École Normale Superieure (ENS) των Παρισίων (Verkerk et al, 1992) και του W. Phillips στο National Institute of Standards and Technology (NIST) του Gaithersburg των ΗΠΑ (Jessen et al, 1992).
Οπτικά πλέγματα μπορούν να κατασκευαστούν για οποιαδήποτε άτομα. Όμως με τα στοιχεία των αλκαλίων η κατασκευή και ο χειρισμός των ατόμων είναι ευκολότερος εξαιτίας της ύπαρξης στην ηλεκτρονική τους δομή ενός μόνο ηλεκτρονίου σθένους. Σε πολύ χαμηλές θερμοκρασίες τα περισσότερα άτομα συμπεριφέρονται με παρόμοιο τρόπο. Το μόνο κρίσιμο στοιχείο είναι αν είναι μποζόνια ή φερμιόνια καθώς με τα πρώτα η διαδικασία επιβράδυνσης της ατομικής κίνησης είναι ευκολότερη. Σήμερα πειράματα με οπτικά πλέγματα εκτελούνται με άτομα διαφόρων στοιχείων όπως τα μποζονικά ρουβίδιο-87, νάτριο-23, κάλιο-39 και κέσιο-13 καθώς και τα φερμιονικά κάλιο-40, λίθιο-6 και στρόντιο-87.
Ο τρόπος με τον οποίο τα άτομα τοποθετούνται σε ένα οπτικό πλέγμα ακολουθεί μια αντίστροφη λογική. Δημιουργούμε πρώτα ένα συμπύκνωμα Bose–Einstein από τα άτομα. Στη συνέχεια σχηματίζουμε αργά το πλέγμα στο χώρο του συμπυκνώματος και τα άτομα αναδιατάσσονται και παίρνουν τις θέσεις τους μέσα στο πλέγμα. Αν θέλουμε να ελευθερώσουμε τα άτομα από τον οπτικό κρύσταλλο τότε, απλά, δεν έχουμε παρά να «σβήσουμε» το οπτικό πλέγμα.
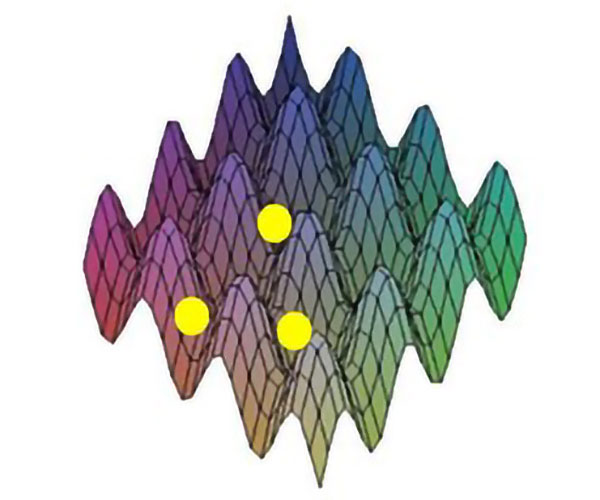
Εικόνα 3. Καλλιτεχνική αναπαράσταση ενός οπτικού πλέγματος και παγιδευμένων ατόμων σε αυτό.
ΟΠΤΙΚΑ ΚΑΙ ΚΡΥΣΤΑΛΛΙΚΑ ΠΛΕΓΜΑΤΑ
Η κίνηση των παγιδευμένων ατόμων σε έναν οπτικό κρύσταλλο προσομοιάζει με την κίνηση των ηλεκτρονίων στο κρυσταλλικό πλέγμα ενός μετάλλου. Σε αυτό ακριβώς το χαρακτηριστικό εδράζεται η σπουδαιότητα των οπτικών κρυστάλλων. Ωστόσο, η ομοιότητα αυτή δεν θα πρέπει να μας οδηγήσει στην παραγνώριση των μεταξύ τους διαφορών, οι οποίες είναι σημαντικές (Cohen-Tannoudji & Guéry-Odelin, 2011). Κατ’ αρχάς στα οπτικά πλέγματα η περιοδικότητα στο χώρο δεν οφείλεται στις αλληλεπιδράσεις μεταξύ των ατόμων αλλά σε ένα εξωτερικό δυναμικό που δημιουργείται από την αλληλεπίδραση των ατόμων με το φως, όπως φαίνεται παραστατικά στην Εικ. 4. Επίσης, η σχετική κλίμακα των χωρικών διαστάσεων είναι διαφορετική. Δύο διαδοχικές θέσεις σε ένα κρυσταλλικό πλέγμα έχουν απόσταση μεταξύ τους της τάξης του Angstrom (10-10 m). Αντίθετα, σε ένα οπτικό πλέγμα η αντίστοιχη απόσταση είναι της τάξης του 1μm (10-6 m), δηλαδή σχεδόν δέκα χιλιάδες φορές μεγαλύτερη. Επιπλέον, τα οπτικά πλέγματα, σε αντιδιαστολή με τα κρυσταλλικά, έχουν χαρακτηριστικά (όπως οι χωρικές διαστάσεις και το ενεργειακό τους βάθος) που μπορούν να μεταβληθούν κατά βούληση με την απλή αλλαγή των τιμών των παραμέτρων των δεσμών λέιζερ που τα δημιουργούν. Η μεγάλη διαφορά κλίμακας μεταξύ των κρυσταλλικών και οπτικών πλεγμάτων έχει ακόμη ένα πλεονέκτημα σε πειραματικό επίπεδο καθώς για να διερευνήσουμε φαινόμενα μέσα σε οπτικό πλέγμα χρειαζόμαστε απλά οπτικά μικροσκόπια σε αντίθεση με ένα κρυσταλλικό πλέγμα στο οποίο χρειαζόμαστε μικροσκόπια ακτινών-Χ. Αντίστοιχης τάξης μεγέθους είναι και η διαφορά στην χρονική διάρκεια αντίστοιχων φαινομένων στα οπτικά και στα κρυσταλλικά πλέγματα. Για παράδειγμα ενώ σε ένα κρυσταλλικό πλέγμα η εκδήλωση του φαινομένου σήραγγας χρειάζεται χρονικά διαστήματα της τάξης του 1 ns (10-9 s) σε ένα οπτικό πλέγμα χρειάζεται μόλις 1 ms (10-3 s). Τέλος, τα οπτικά πλέγματα είναι, στις περισσότερες περιπτώσεις, απαλλαγμένα από τα φωνόνια (phonons), τις συλλογικές ταλαντώσεις ατόμων στις περιοδικές δομές των κρυστάλλων των στερεών σωμάτων.
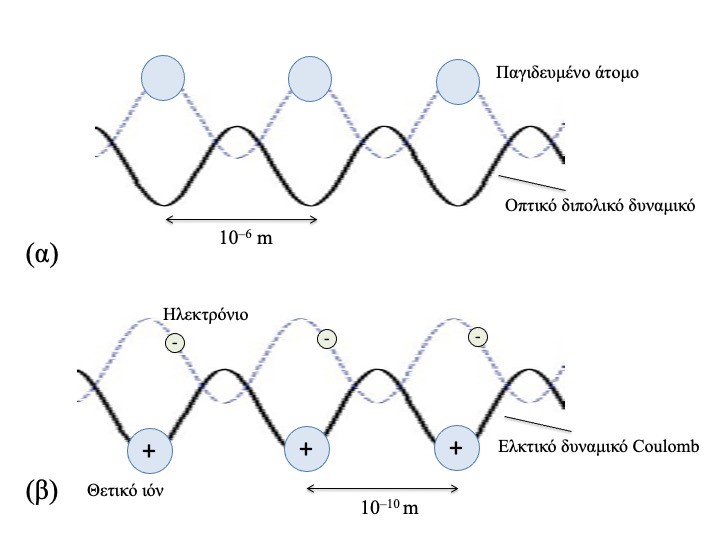
Εικόνα 4. Άτομα σε οπτικό πλέγμα και ηλεκτρόνια σε κρυσταλλικό πλέγμα. Οι γαλάζιες διακεκομμένες καμπύλες στο οπτικό πλέγμα αναπαριστούν τις κυματοσυναρτήσεις των ατόμων και αντιστοιχούν σε εκείνες των ηλεκτρονίων σθένους σε ένα πραγματικό κρύσταλλο (Greiner et al, 2015).
ΙΜΑΝΤΕΣ ΜΕΤΑΦΟΡΑΣ ΓΙΑ ΑΤΟΜΑ
Ένα άλλο ενδιαφέρον χαρακτηριστικό των οπτικών κρυστάλλων είναι η δυνατότητα μετακίνησής τους στο χώρο. Πράγματι, οι θέσεις των μέγιστων και ελάχιστων της έντασης και του διπολικού δυναμικού μπορούν να μετακινηθούν πάνω στη διεύθυνση διάδοσης των δεσμών λέιζερ. Ακόμη πιο ενδιαφέρον είναι ο τρόπος που επιτυγχάνεται κάτι τέτοιο: απλά μεταβάλλοντας ελαφρά τη συχνότητα του ενός από τα δύο λέιζερ! Για παράδειγμα, αν μεταξύ των δύο δεσμών υπάρχει μια διαφορά συχνοτήτων, Δf =f1-f2, τότε το οπτικό πλέγμα μετακινείται στο χώρο με μια ταχύτητα v = λΔf/2. Μάλιστα μπορεί να μετακινηθεί τόσο προς τη θετική κατεύθυνση (εάν Δf > 0) όσο και προς την αρνητική (εάν Δf < 0). Με αυτόν τον τρόπο τα μετακινούμενα πλέγματα λειτουργούν ως οπτικοί ιμάντες μεταφοράς (optical conveyors) για τα παγιδευμένα άτομα (Schrader et al, 2001). Οι οπτικοί ιμάντες μεταφοράς χρησιμοποιούνται για τη μεταφορά ενός συνόλου ψυχρών ατόμων μεταξύ δύο σημείων του χώρου ενώ παράλληλα τα άτομα παραμένουν παγιδευμένα και βραδυκίνητα. Αυτός ο μηχανισμός μεταφοράς ατόμων στο χώρο έχει αξιοποιηθεί στη λειτουργία των ατομικών ρολογιών (atomic clocks) (Riis et al, 1990), (Clairon et al, 1991), στην δημιουργία ατομοπομπών από ψυχρά άτομα (Weyers et al, 1997), (Cren et al, 2002) και στην συντεταγμένη μεταφορά ενός μεγάλου αριθμού ατόμων ανάμεσα σε συγκεκριμένες θέσεις στο εσωτερικό μιας οπτικής ίνας (Langbecker et al, 2018).
Αν εκμεταλλευτούμε την πλούσια εσωτερική ενεργειακή δομή των ατόμων μπορούμε να κατασκευάσουμε ιμάντες μεταφοράς με ακόμη μεγαλύτερες δυνατότητες (Mandel et al, 2003). Όπως γνωρίζουμε, από την ατομική φυσική, ένα άτομο έχει σε κάθε ενεργειακή του κατάσταση αρκετές υποστάθμες Zeeman (Zeeman sublevels). Όταν τα άτομα βρίσκονται σε διαφορετικές υποστάθμες, τότε υπόκεινται σε ένα διαφορετικό οπτικό διπολικό δυναμικό. Φωτίζοντας το άτομο με δύο γραμμικά πολωμένες δέσμες λέιζερ, όπου οι πολώσεις τους σχηματίζουν γωνία , όπως φαίνεται στην Εικ. 5, δημιουργούμε ένα οπτικό πεδίο που είναι ισοδύναμο με αυτό που παράγεται από την συμβολή δύο στάσιμων κύματα με αντίθετες κυκλικές πολώσεις και τα οποία είναι μετατοπισμένα στο χώρο κατά μια απόσταση . Τα άτομα, λοιπόν, που βρίσκονται σε διαφορετικές υποστάθμες Zeeman, αισθάνονται την επίδραση διαφορετικών δυναμικών και παγιδεύονται σε διαφορετικές περιοχές του χώρου. Η μεταξύ τους απόσταση όμως, ευτυχώς για εμάς, εξαρτάται από τη γωνία . Ελαττώνοντας αυτή τη γωνία μπορούμε να τα φέρουμε όσο πιο κοντά θέλουμε. Τα οπτικά πλέγματα αυτού του τύπου έχουν παίξει κεντρικό ρόλο στην ανάπτυξη ατομικών κβαντικών πυλών (atomic quantum gates) όπως θα δούμε στο δεύτερο μέρος του αφιερώματός μας στους οπτικούς κρυστάλλους.
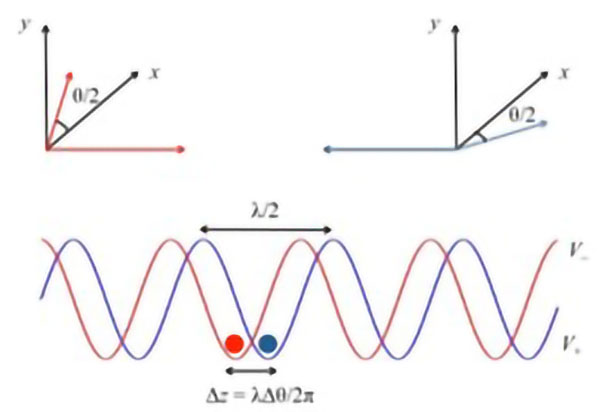
Εικόνα 5. Η συμβολή δύο δεσμών που διαδίδονται σε αντίθετες κατευθύνσεις και έχουν πολώσεις οι οποίες σχηματίζουν μια γωνία μας δίνει ένα οπτικό πεδίο το οποίο είναι ισοδύναμο με αυτό δύο στάσιμων κυμάτων με δεξιόστροφη κυκλική πόλωση σ+ και αριστερόστροφη κυκλική πόλωση σ– αντίστοιχα. Τα δύο στάσιμα κύματα είναι χωρικά μετατοπισμένα κατά μια απόσταση. Ως αποτέλεσμα τα άτομα βρίσκονται εντός διαφορετικών οπτικών πλεγμάτων με δυναμικά V+ και V– αντίστοιχα.
ΜΕΓΑΛΗ ΠΟΙΚΙΛΙΑ ΜΟΡΦΩΝ
Τα οπτικά πλέγματα χαρακτηρίζονται από μεγάλη γεωμετρική ποικιλότητα καθώς έχουμε τη δυνατότητα διαφορετικών επιλογών, όσον αφορά στην κατεύθυνση των δεσμών, στην ένταση και στην πόλωσή τους. Για παράδειγμα, αν οι δύο δέσμες λέιζερ διαδίδονται σε κατευθύνσεις που σχηματίζουν μια γωνία μεταξύ τους, η οποία μπορεί να μεταβάλλεται κατά βούληση, τότε μπορούμε να ρυθμίζουμε τη σχετική απόσταση μεταξύ των δεσμών και κοιλιών του στάσιμου κύματος που προκύπτει από τη συμβολή των δεσμών και άρα των θέσεων που μπορούν να παγιδευτούν τα άτομα. Ποιο περίπλοκες δομές οπτικών πλεγμάτων, όπως εξαγωνικές και εδροκεντρωμένες κυβικές, είναι επίσης δυνατές και παράγονται σχετικά εύκολα σε ένα εργαστήριο οπτικής (Εικ. 6) (Grynberg et al, 1993).
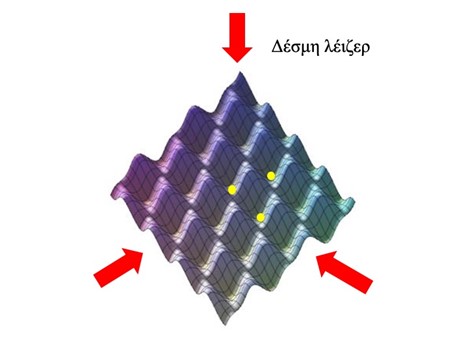
Εικόνα 6. Τρεις συμβάλλουσες ομοεπίπεδες δέσμες που διαδίδονται σε κατευθύνσεις που σχηματίζουν διαδοχικά γωνίες 120ο μοιρών δημιουργούν ένα οπτικό πλέγμα δύο διαστάσεων με εξαγωνική γεωμετρία. Στη βιβλιογραφία αναφέρεται ως οπτικό πλέγμα γραφενίου εξαιτίας της ομοιότητας του με τη δομή του διάσημου πλέον υλικού.
H αξιοποίηση δεσμών λέιζερ με φωτόνια που φέρουν και στροφορμή κατά μήκος του άξονα διάδοσης, γνωστών με τον όρο οπτικοί στρόβιλοι, έδωσε νέες ποικιλίες οπτικών πλεγμάτων. Αυτά τα πλέγματα χαρακτηρίζονται από κυλινδρική συμμετρία. Σχηματίζονται από οπτικούς στρόβιλους που διαδίδονται στην ίδια κατεύθυνση αλλά έχουν φωτόνια με αντίθετη τροχιακή στροφορμή ±lħ (όπου l ένας ακέραιος αριθμός, γνωστός ως τοπολογικό φορτίο (topological charge) ή αριθμός περιέλιξης (winding number) και ħ η ανηγμένη σταθερά του Planck, ħ=h/2π). Τα πλέγματα αυτά μπορούν να λειτουργήσουν ως ιμάντες περιφοράς καθώς μια διαφορά στις συχνότητες των δύο δεσμών ίση με Δf είναι ικανή να περιστρέψει το πλέγμα με μια γωνιακή ταχύτητα Ω = πΔf/l (Franke-Arnold et al, 2007). Μεταβάλλοντας το πρόσημο της διαφοράς συχνοτήτων μπορούμε να περιστρέψουμε τον ιμάντα προς τη μια ή την άλλη διεύθυνση.
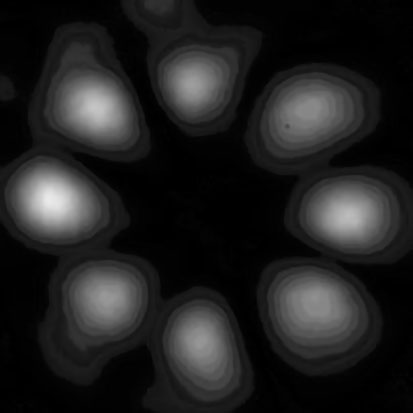

Εικόνα 7. Αριστερά. Ο οπτικός τροχός του Ferris (από τον ομώνυμο τροχό των λούνα-πάρκ). Το προφίλ της έντασης ενός οπτικού τροχού του Ferris που έχει παραχθεί από τη συμβολή οπτικών στροβίλων με τοπολογικούς αριθμούς l= ±4 οι οποίοι διαδίδονται στην ίδια κατεύθυνση. Δεξιά. Το οπτικό «ρεβόλβερ» είναι ένα παράδειγμα οπτικού πλέγματος με κυλινδρική συμμετρία κατασκευασμένο από τη συμβολή οπτικών στροβίλων με διαφορετικά τοπολογικά φορτία. Η διεύθυνση διάδοσης των οπτικών στροβίλων είναι από την εικόνα προς τον αναγνώστη. Οι φωτογραφίες είναι ευγενική προσφορά προς το InS της Ερευνητικής Ομάδας Οπτικής του Πανεπιστημίου της Γκλασκώβης.
Αν οι δύο συμβάλλοντες οπτικοί στρόβιλοι έχουν και αντίθετη διεύθυνση διάδοσης τότε έχουμε μια τρισδιάστατη εκδοχή του παραπάνω μηχανισμού. Σε αυτήν την περίπτωση τα άτομα παγιδεύονται μέσα σε ελικοειδείς σωλήνες. Όταν δε, οι δύο δέσμες έχουν ελαφρώς διαφορετική συχνότητα, τότε το πεδίο αυτό περιστρέφεται και μπορεί να παρασύρει παγιδευμένα σωματίδια και άτομα λειτουργώντας για αυτά όπως μια σπείρα του Αρχιμήδη η οποία χρησιμοποιείται, ακόμη και σήμερα, για την άντληση νερού από ποτάμια και λίμνες προς άρδευση γεωργικών καλλιεργειών και οικιακών χρήσεων.
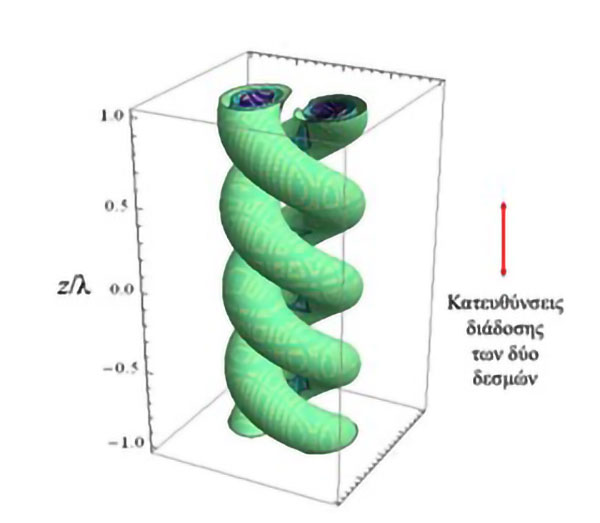
Εικόνα 8. Μια οπτική σπείρα του Αρχιμήδη. Η ένταση του φωτός χαρακτηρίζεται από μια ελικοειδή δομή στο χώρο. Στη συγκεκριμένη περίπτωση οι αριθμοί περιέλιξης των δεσμών είναι l = ±1 με αποτέλεσμα η έλικα να διαγράφει μια περιστροφή 360ο μέσα σε μια απόσταση ίση με το μήκος κύματος του φωτός. Με μια ελαφρά μεταβολή της συχνότητας μιας εκ των δύο συμβαλλουσών δεσμών το σύστημα αυτό περιστρέφεται στο χώρο παρασύροντας παγιδευμένα άτομα και σωματίδια προς τα πάνω ή προς τα κάτω (Al Rsheed et al, 2016).
ΔΙΕΡΕΥΝΗΣΗ ΘΕΜΕΛΙΩΔΩΝ ΚΒΑΝΤΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ
Αναφερθήκαμε νωρίτερα στο κβαντικό φαινόμενο σήραγγας. Πρόκειται για ένα φαινόμενο που λαμβάνει χώρα όταν ένα σωμάτιο μπορεί να μετακινηθεί ανάμεσα σε δύο θέσεις, οι οποίες διαχωρίζονται από ένα φράγμα δυναμικής ενέργειας, ακόμη και όταν δεν έχει την απαιτούμενη κινητική ενέργεια για να υπερνικήσει τον φραγμό. Ένα άτομο παγιδευμένο σε ένα οπτικό πλέγμα αποτελεί ιδανικό σύστημα για να παρατηρήσουμε το φαινόμενο σήραγγας (Εικ.9). Μεταβάλλοντας την ένταση του στάσιμου κύματος αλλάζουμε το βάθος του οπτικού δυναμικού στο οποίο παγιδεύονται τα άτομα, άρα και το ύψος του φραγμού δυναμικής ενέργειας ανάμεσα σε δύο γειτονικές θέσεις του οπτικού πλέγματος. Με αυτόν τον τρόπο μπορούμε να ελέγχουμε το ρυθμό με τον οποίο τα άτομα περνούν από τη μια θέση στην άλλη αξιοποιώντας το φαινόμενο σήραγγας. Αυτό δίνει τη δυνατότητα να διερευνούμε το όριο ανάμεσα στην κατάσταση που τα άτομα είναι πλήρως εντοπισμένα στα “φρεάτια” δυναμικού του πλέγματος και στην κατάσταση που “ελευθερώνονται” από αυτά και κινούνται ελεύθερα στο πλέγμα. Σε αυτήν την περίπτωση έχουμε έναν ιδανικό προσομοιωτή για τη μετάβαση από μια κατάσταση όπου ένα σύστημα συμπεριφέρεται ως μονωτής, σε μια κατάσταση υπερρευστότητας για την οποία θα μιλήσουμε εκτενώς στο επόμενο σχετικό άρθρο (Greiner et al, 2002), (Schneider et al, 2008).

Εικόνα 9. Καλλιτεχνική αναπαράσταση του φαινόμενου σήραγγας. Ευγενική προσφορά στο InS του I. Bloch, καθηγητή στο Πανεπιστήμιο Ludwig Maximilian (LMU) του Μονάχου και Διευθυντή Ερευνών στο Ινστιτούτο Max Planck για την Κβαντική Οπτική στο Garching της Γερμανίας.
Τα οπτικά πλέγματα έχουν αποδειχθεί ιδανικά πεδία για την αποθήκευση και επεξεργασία κβαντικής πληροφορίας. Αυτό οφείλεται στη δυνατότητα επιλεκτικής αλληλεπίδρασης με συγκεκριμένα άτομα σε διάφορες θέσεις του οπτικού πλέγματος για να καταχωρούμε ή να ανακτούμε την πληροφορία από αυτά (Εικ.10). Το άτομο χρησιμοποιείται με τον ίδιο τρόπο που ένα μεμονωμένο μπιτ χρησιμοποιείται σε έναν καταγραφέα (register) ενός κλασικού υπολογιστή. Τα πρώτα πειράματα σε αυτήν την κατεύθυνση έγιναν στο Νational Institute of Standards & Technology (NIST) των ΗΠΑ από την ομάδα του W. Phillips (Porto et al, 2003) και στη Βόννη από την ομάδα του D. Meschede (Schrader et al, 2004). Σήμερα μπορούμε να επιλέγουμε, στην κυριολεξία, όποια θέση θέλουμε σε ένα οπτικό πλέγμα, να τοποθετούμε ένα άτομο σε αυτήν και στη συνέχεια να το φέρουμε σε αλληλεπίδραση με μια δέσμη λέιζερ τα χαρακτηριστικά της οποίας είναι πλήρως ελεγχόμενα από εμάς. H επιλεκτική αλληλεπίδραση απαιτεί την χρήση ισχυρά εστιασμένων δεσμών λέιζερ ώστε να μη διαταράσσονται τα γειτονικά άτομα. Οι τεχνικές αυτές έχουν αξιοποιηθεί στην υλοποίηση πυλών για κβαντικούς υπολογιστές. Η Εικ.11 μας δείχνει ένα μικρό δείγμα από τις σχεδόν απεριόριστες δυνατότητες που έχουμε σήμερα στην κατά βούληση τοποθέτηση ατόμων σε διαφορετικές θέσεις ενός οπτικού πλέγματος.
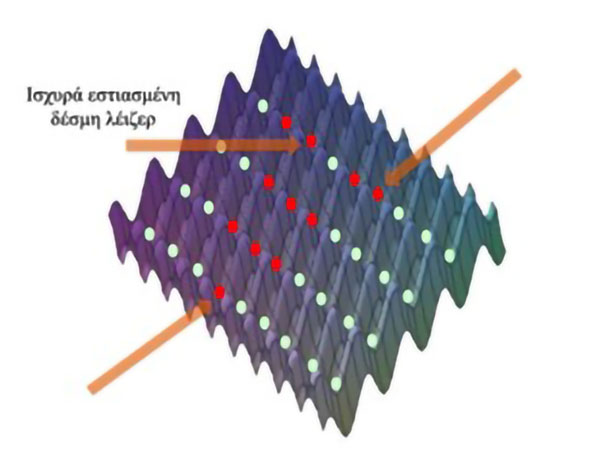
Εικόνα 10. Καλλιτεχνική αναπαράσταση της δυνατότητας επιλεκτικής αλληλεπίδρασης με μεμονωμένα άτομα στοχεύοντάς τα με ισχυρά εστιασμένες δέσμες λέιζερ.

Εικόνα 11. Εικόνες από μεμονωμένα άτομα που έχουν τοποθετηθεί σε διάφορες θέσεις μέσα σε οπτικό πλέγμα. Ευγενική προσφορά στο InS του I. Bloch, καθηγητή στο Πανεπιστήμιο Ludwig Maximilian (LMU) του Μονάχου και Διευθυντή Ερευνών στο Ινστιτούτο Max Planck για την Κβαντική Οπτική στο Garching της Γερμανίας
Αφήσαμε για το τέλος αυτού του άρθρου την πιο σημαντική εφαρμογή των οπτικών πλεγμάτων στη μελέτη των θεμελιωδών εννοιών της κβαντικής φυσικής. Η στατιστική ερμηνεία της κβαντικής μηχανικής ορίζει ως μέση τιμή ενός κβαντομηχανικού μεγέθους τη μέση τιμή που παίρνουμε έπειτα από διαδοχικές μετρήσεις πάνω σε ένα ή περισσότερα σωματίδια. Απαραίτητη προϋπόθεση είναι πριν από κάθε μέτρηση το σύστημα των ατόμων να έχει προετοιμαστεί στην ίδια αρχική κατάσταση (Haroche & Raimond, 2006). Στην περίπτωση ενός κβαντικού συστήματος όλη η πληροφορία για αυτό εμπεριέχεται στην κυματοσυνάρτησή του Ψ. Η εκ νέου προετοιμασία είναι αναγκαία καθώς, μετά από κάθε μέτρηση, επέρχεται η λεγόμενη κατάρρευση της κυματοσυνάρτησης (collapse of the wave function), δηλαδή η απώλεια όλων των υπόλοιπων εν δυνάμει αποτελεσμάτων που θα μπορούσαν να προκύψουν από τη μέτρηση. Σύμφωνα με το αξίωμα της μέτρησης: οποιαδήποτε κι αν ήταν η κατάσταση ενός κβαντικού συστήματος πριν από μια μέτρηση, η κατάσταση μετά τη μέτρηση θα περιγράφεται από την ιδιοσυνάρτηση που αντιστοιχεί στην ιδιοτιμή η οποία μετρήθηκε (Τραχανάς, 2008). Με άλλα λόγια, στην κβαντική φυσική η μέτρηση είναι μια ενδογενώς μη αντιστρεπτή διαδικασία καθώς το σύστημα παραμένει, πλέον, σε μια κατάσταση που αντιστοιχεί στην ιδιοτιμή της ενέργειας που έχει μετρηθεί.
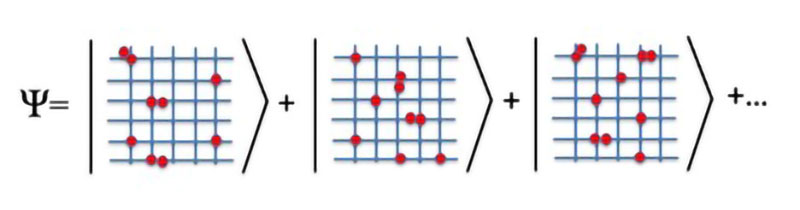
Εικόνα 12. H κατάσταση ενός πολυσωματιδιακού κβαντικού συστήματος είναι μια υπέρθεση (superposition) διαφορετικών εν δυνάμει σχηματισμών. Κάθε φορά που λαμβάνουμε μια φωτογραφία του συστήματος αυτό «καταρρέει» σε έναν από αυτούς τους σχηματισμούς. Κάτι τέτοιο είναι αδύνατο σε ένα σύνηθες κρυσταλλικό πλέγμα. Με ένα πολυάριθμο σύνολο τέτοιων φωτογραφικών απεικονίσεων «ανασυνθέτουν» οι πειραματικοί την ολική κατάσταση του συστήματος.
Η δυνατότητα να τοποθετούμε εκατοντάδες, πλέον, άτομα σε οποιαδήποτε αρχική θέση σε ένα οπτικό πλέγμα και να αλληλεπιδρούμε επιλεκτικά με αυτά, επιτρέπει την πλήρη ανακατασκευή της κυματοσυνάρτησης Ψ του συστήματος και τον υπολογισμό όχι μόνο μέσων τιμών αλλά και των κβαντικών διακυμάνσεων ενός συστήματος μεγάλου αριθμού ατόμων (Greiner et al, 2015). Ειδικά σε συστήματα ισχυρώς αλληλεπιδρώντων σωματιδίων η ουσιαστική πληροφορία δεν “κρύβεται” στις μέσες τιμές αλλά στις διακυμάνσεις και τις κβαντικές συσχετίσεις, οι οποίες για πρώτη φορά σήμερα είναι πειραματικά προσπελάσιμες. Πως γίνεται κάτι τέτοιο; Απλά με ταχύτατη φωτογράφιση του συστήματος πάρα πολλές φορές και εφόσον, πριν από κάθε νέα φωτογράφιση, αυτό έχει ετοιμαστεί στην αρχική του κατάσταση. Κάθε φωτογράφιση αποκαλύπτει μια από τις εν δυνάμει καταστάσεις του συστήματος. Μετά το πέρας των φωτογραφήσεων οι πειραματικοί έχουν στα χέρια τους την στατιστική κατανομή των διαφόρων καταστάσεων και από αυτήν «ανασυνθέτουν» την κυματοσυνάρτηση του συστήματος (Εικ. 11). Οι ερευνητές έχουν ήδη πραγματοποιήσει αξιοσημείωτη πρόοδο στην ανασύνθεση της κυματοσυνάρτησης ενός πολύπλοκου συστήματος όπως, για παράδειγμα, στην πρόσφατη περίπτωση ενός συνόλου από εκατό χιλιάδες άτομα υττερβίου που είχαν παγιδευτεί σε ένα οπτικό πλέγμα (Subhankar et al, 2019). Αν ο πλήρης έλεγχος απλών κβαντικών συστημάτων είναι ήδη μια πραγματικότητα (Haroche & Raimond, 2006) οι ερευνητές βαδίζουν ταχύτατα προς τον απόλυτο έλεγχο πολυσωματιδιακών κβαντικών συστημάτων.
Στο δεύτερο μέρος του αφιερώματος μας στους οπτικούς κρυστάλλους θα δούμε αναλυτικότερα με ποιους τρόπους αυτά τα φυσικά συστήματα έχουν ανοίξει νέους ορίζοντες στην ατομική φυσική και στην απρόσμενη συνάντησή της με την φυσική της συμπυκνωμένης ύλης .
ΒΙΒΛΙΟΓΡΑΦΙΑ
Τραχανάς, Σ., 2008. ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ ΙΙ: ΘΕΜΕΛΙΩΔΕΙΣ ΑΡΧΕΣ ΚΑΙ ΜΕΘΟΔΟΙ. ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ. Ηράκλειο: Πανεπιστημιακές Εκδόσεις Κρήτης, σ. 592.
Al Rsheed, A., Lyras, A., Lembessis V., E., Aldossary, O., M., 2016. Guiding of atoms in helical optical potential structures. J. Phys. B: At. Mol. Opt. Phys. 49 (12), 125002. 10.1088/0953-4075/49/12/125002
Bloch, I., 2005. Ultracold atoms in quantum gases. Nature Physics 1, p. 23. 10.1038/nphys138
Clairon, A., Salomon, C., Guellati, S., and Phillips, W., D., 1991. Ramsey Resonance in a Zacharias Fountain. Europhys. Lett. 16, p. 165. 10.1209/0295-5075/16/2/008
Cohen-Tannoudji, C., and D. Guéry-Odelin, D., 2011. ADVANCES IN ATOMIC PHYSICS: An overview. New Jersey: World Scientific, p.335. https://www.worldscientific.com/worldscibooks/10.1142/6631
Cren, P., Roos, C., F., Aclan, A., Dalibard, J., and Guéry-Odelin, D., 2002. Loading of a cold atomic beam into a magnetic guide. Eur. Phys. J. D. 20, p. 107. https://doi.org/10.1140/epjd/e2002-00106-3
De Mello, D., O., Schäffner, D., Werkmann, J., Preuschoff, T., Kohfahl, L., Schlosser, M. and Birkl, G., 2019. Defect-Free Assembly of 2D Clusters of More Than 100 Single-Atom Quantum Systems. Phys. Rev. Lett. 122, 203601. https://doi.org/10.1103/PhysRevLett.122.203601
Franke-Arnold, S., Leach, J., Padgett, M., J., Lembessis, V., E., Ellinas, D., Wright, A., J., Girkin, J., M., Öhberg, P., and Arnold, A., S., 2007. Optical Ferris wheel for ultracold atoms. Optics Express 15, p. 8619. https://doi.org/10.1364/OE.15.008619
Greiner, Μ., Mandel, Ο., Esslinger, Τ., Hänsch, Τ., W., and Bloch, I., 2002. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, p. 39. https://doi.org/10.1038/415039a
Greiner, M., and I. Bloch, I., 2015. Quantengase unter den Mikroskop (Quantum Gases under the Microscope). Physik Journal 14, Nr. 10, p. 33. https://www.pro-physik.de/restricted-files/86861
Grynberg, G., Lounis, B., Verkerk, P., Courtois, J.-Y., and Salomon, C., 1993. Quantized motion of cold cesium atoms in two- and three-dimensional optical potentials. Phys. Rev. Lett. 70, p. 2249. https://doi.org/10.1103/PhysRevLett.70.2249
Haroche, S. and Raimond, 2006. Exploring the Quantum: Atoms, Cavities, and Photons, Oxford: Oxford University Press. https://oxford.universitypressscholarship.com/view/10.1093/acprof:oso/9780198509141.001.0001/acprof-9780198509141
Jessen, P., S., Gerz, C., Lett, P., D., Phillips, W., D., Rolston S., L., Spreeuw, R., J., C., and Westbrook, C., I., 1992. Observation of quantized motion of Rb atoms in an optical field. Phys. Rev. Lett. 69, p. 49. https://doi.org/10.1103/PhysRevLett.69.49
Langbecker, M., Wirtz, R., Knoch, B., Noaman, M., Speck, T., and Windpassinger, P., 2018. Highly controlled optical transport of cold atoms into a hollow-core fiber. New. J. Phys. 20, 083038. https://doi.org/10.1088/1367-2630/aad9bb
Mandel, O., Greiner, M., Widera, A., Rom, T., Hänsch, T. W., and Bloch, I., 2003. Coherent Transport of Neutral Atoms in Spin-Dependent Optical Lattice Potentials. Phys. Rev. Lett. 91, 010407. https://doi.org/10.1103/PhysRevLett.91.010407
Porto, J., V., Rolston, S., Laburthe Tolra, B., Williams, C., J., and Phillips, W., D., 2003. Quantum information with neutral atoms as qubits. Phil. Trans. R. Soc. A. 361, p.1417. http://doi.org/10.1098/rsta.2003.1211
Riis, E., Weiss, D., Moler, K., and Chu, S., 1990. Atom funnel for the production of a slow, high-density atomic beam. Phys. Rev. Lett. 64, p. 1658. 10.1103/PhysRevLett.64.1658
Schneider, U., Hackermüller, L., Will, S., Best, Th., Bloch, I., Costi, T., A., Helmes, R., W., Rasch, D., and Rosch, A., 2008. Metallic and insulating phases of repulsively interacting fermions in a 3D optical lattice. Science 322, p. 1520. DOI: 10.1126/science.1165449
Schrader, D., Kuhr, S., Alt, W., Müller, M., Gomer, V., and Meschede, D., 2001. An optical conveyor belt for single atoms. Appl. Phys. B 73, p. 819. https://doi.org/10.1007/s003400100722
Schrader, D., Dotsenko, I., Khudaverdyan, M., Miroshnychenko, Y., Rauschenbeutel, A., and Meschede D., 2004. Neutral atom quantum register. Phys. Rev. Lett. 93, 150501. https://doi.org/10.1103/PhysRevLett.93.150501
Subhankar, S., Wang, Y., Tsui, T.-C., Rolston, S., L., and Porto, J., V., 2019. Nanoscale Atomic Density Microscopy. Phys. Rev. X 9, 021002. https://doi.org/10.1103/PhysRevX.9.021002
Verkerk, P., Lounis, B., Salomon, C., Cohen-Tannoudji, C., Courtois, J.-Y., and Grynberg, G., 1992. Dynamics and spatial order of cold cesium atoms in a periodic optical potential. Phys. Rev. Lett. 68, p. 3861. https://doi.org/10.1103/PhysRevLett.68.3861
Weyers, S., Aucouturier, E., Valentin, C., and Dimarcq, N., 1997. A continuous beam of cold cesium atoms extracted from a two-dimensional magneto-optical trap. Opt. Comm. 143, p. 30. https://doi.org/10.1016/S0030-4018(97)00312-X




