Το 2018 η Σουηδική Ακαδημία Επιστημών τίμησε με το βραβείο Νόμπελ τον Αμερικανό φυσικό Αrthur Ashkin για “το πρωτοποριακό ερευνητικό του έργο στις οπτικές λαβίδες και τις εφαρμογές τους στη βιολογία”, όπως λιτά και περιεκτικά ανέφερε η ανακοίνωση. Ο Ashkin εφεύρε τις οπτικές λαβίδες οι οποίες αποτελούν ένα εξαιρετικά αποτελεσματικό εργαλείο το οποίο, με τη βοήθεια φωτός λέιζερ, μας επιτρέπει να χειριζόμαστε την κίνηση ατόμων, σωματιδίων, ιών και κυττάρων ανοίγοντας το δρόμο για πρωτόγνωρες και επαναστατικές εφαρμογές. Στις βασικές αρχές λειτουργίας και τις κυριότερες εφαρμογές των οπτικών λαβίδων αναφέρεται αυτό το άρθρο.
Με τον όρο “λαβίδα” εννοούμε συνήθως ένα εργαλείο το οποίο μας βοηθάει να χειριζόμαστε πράγματα τα οποία δεν είναι δυνατόν, για διάφορους λόγους, να τα αγγίξουμε με γυμνό χέρι. Πολλές φορές ο χειρισμός των λαβίδων απαιτεί ιδιαίτερα λεπτές κινήσεις και αυξημένη επιδεξιότητα γιατί είναι πιθανόν να ελλοχεύουν διάφοροι κίνδυνοι. Κλασικό παράδειγμα η περίπτωση της χειρουργικής ιατρικής όπου οι γιατροί έρχονται, μέσω των λαβίδων, σε επαφή με πολύ ευαίσθητα όργανα. Τα περισσότερα, όμως, παραδείγματα χρήσης λαβίδων, σε τελική ανάλυση, αφορούν στο χειρισμό αντικειμένων της καθημερινής μας ζωής ή, όπως επιστημονικά καλούμε, του μακρόκοσμου. Στις μέρες μας αναπτύσσονται τεχνικές οι οποίες μας δίνουν την δυνατότητα κατασκευής λαβίδων για το μικρόκοσμο. Πρόκειται για μηχανισμούς με την βοήθεια των οποίων μπορούμε και χειριζόμαστε την κίνηση και τη θέση σωματιδίων με διαστάσεις από μερικά χιλιοστά έως και μερικά δισεκατομμυριοστά του μέτρου όπως πολύ παραστατικά φαίνεται στην Εικ.1. Η λειτουργία αυτών των μηχανισμών βασίζεται στην αλληλεπίδραση φωτός λέιζερ με τα σωματίδια γι’ αυτό και είναι γνωστοί, στην διεθνή βιβλιογραφία, με τον όρο οπτικές λαβίδες (optical tweezers).
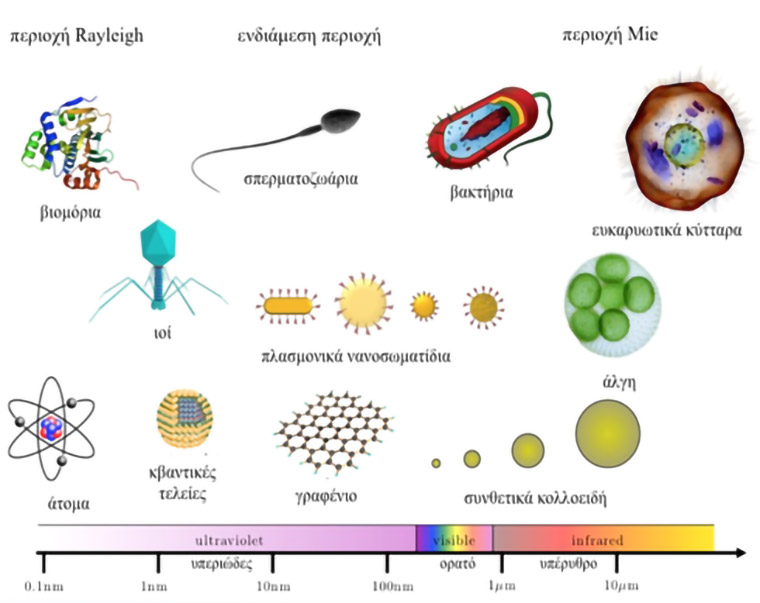
Εικόνα 1: Η κλίμακα των σωματιδίων, τα οποία μπορούμε να χειριστούμε με οπτικές λαβίδες και κάποια τυπικά παραδείγματα από αυτά. Η κλίμακα δίνεται σε τιμές των μηκών κύματος του φωτός, το οποίο χρησιμοποιείται για την παγίδευση των σωματιδίων (Jones, 2016).
Η ΑΡΧΗ ΛΕΙΤΟΥΡΓΙΑΣ
Για να κατανοήσουμε τη φυσική των οπτικών λαβίδων θα πρέπει να διακρίνουμε δύο βασικές περιπτώσεις. Η διάκριση αυτή καθορίζεται από το λόγο της διαμέτρου δ του σωματιδίου ως προς το μήκος κύματος λ της δέσμης του φωτός που χρησιμοποιούμε. Στην περίπτωση που το μέγεθος του σωματιδίου είναι αρκετά μεγαλύτερο από το μήκος κύματος (δ/λ>>1), η αλληλεπίδραση σωματιδίου -δέσμης μπορεί να περιγραφεί με όρους γεωμετρικής οπτικής (σκέδαση Mie). Στην αντίθετη περίπτωση (δ/λ<<1), η αλληλεπίδραση σωματιδίου – δέσμης μπορεί να περιγραφεί με όρους κυματικής οπτικής (σκέδαση Rayleigh). Στο ενδιάμεσο όριο, όπου το μέγεθος του σωματιδίου είναι συγκρίσιμο με το μήκος κύματος, η μελέτη της αλληλεπίδρασης απαιτεί αναλυτική επίλυση των εξισώσεων Maxwell.
Εν γένει, οι δυνάμεις που ασκεί μια οπτική λαβίδα σε ένα σωματίδιο είναι (σε μεγάλο βαθμό) δύο ειδών: (α) Η δύναμη που προέρχεται από απορρόφηση και ανάκλαση φωτονίων, οπότε σχετίζεται με την αρχή διατήρηση της ορμής και ονομάζεται δύναμη σκέδασης (scattering force). Η δύναμη αυτή μπορεί να επιβραδύνει ή να επιταχύνει την ατομική κίνηση, είναι ανάλογη της ισχύος του λέιζερ και κυριαρχεί στην περίπτωση που το μέγεθος του σωματιδίου είναι αρκετά μεγαλύτερο από το μήκος κύματος του λέιζερ. (β) Η δύναμη που προέρχεται από την πόλωση του σωματιδίου μέσα στο ηλεκτρικό πεδίο του λέιζερ, γνωστή ως οπτική διπολική δύναμη (optical dipole force) η οποία είναι συντηρητική δύναμη και προέρχεται από μια δυναμική ενέργεια (γνωστή ως οπτική δυναμική ενέργεια) που είναι ανάλογη της έντασης της δέσμης λέιζερ. Η δύναμη αυτή κυριαρχεί στην περίπτωση που το μέγεθος του σωματιδίου είναι πολύ μικρότερο από το μήκος κύματος και είναι υπεύθυνη για τον περιορισμό (παγίδευση) του σωματιδίου σε μια περιοχή του χώρου.
Η λειτουργία των οπτικών λαβίδων, στην περίπτωση μεγάλων σωματιδίων, είναι δυνατόν να ερμηνευθεί και με βάση την κυματική φύση του φωτός καθώς, σε αυτήν την περίπτωση το μήκος κύματος είναι πολύ μικρό σε σύγκριση με τις διαστάσεις του σωματιδίου οπότε η δέσμη λέιζερ μπορεί να θεωρηθεί ως μια δέσμη ακτινών γεγονός που μας επιτρέπει να καταφύγουμε στα εργαλεία της γεωμετρικής οπτικής. Εδώ το κυρίαρχο φυσικό φαινόμενο είναι η διάθλαση του φωτός. Στις οπτικές λαβίδες φροντίζουμε τα σωματίδια να είναι διαφανή και ο δείκτης διάθλασής τους να είναι υψηλότερος από αυτόν του μέσου μέσα στο οποίο τα σωματίδια είναι εμβαπτισμένα. Με άλλα λόγια το σωματίδιο λειτουργεί, στην ουσία, σαν ένας φακός για τη φωτεινή δέσμη. Όταν λοιπόν η πορεία του φωτός αλλάξει, καθώς περνά μέσα από το σωματίδιο, ταυτόχρονα μεταβάλλεται και η ορμή-ενέργειά της δέσμης. Λόγω της αρχής διατήρησης της ορμής, μια ίση και αντίθετη μεταβολή θα προκληθεί στην ορμή του σωματιδίου. Αυτό έχει σαν συνέπεια να ασκηθεί μια δύναμη στο σωματίδιο.
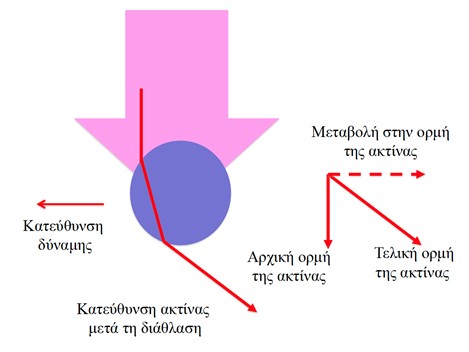
Εικόνα 2: Η προέλευση της δύναμης που ασκεί η οπτική λαβίδα σε ένα σωματίδιο μεγάλων διαστάσεων σε σύγκριση με το μήκος κύματος. Το σωματίδιο διαθλά το φως αλλάζοντάς του την κατεύθυνση άρα και την ορμή. Σύμφωνα με τον τρίτο νόμο του Νεύτωνα, το σωματίδιο θα μεταβάλλει στην αντίθετη κατεύθυνση την ορμή του. Συνεπώς θα ασκηθεί στο σωματίδιο μια δύναμη.
Στην περίπτωση που το σωματίδιο έχει μικρές διαστάσεις σε σύγκριση με το μήκος κύματος τότε πολώνεται ηλεκτρικά εξαιτίας του ηλεκτρομαγνητικού πεδίου της δέσμης λέιζερ. Λόγω του μικρού μεγέθους ο κυρίαρχος όρος είναι ο διπολικός και το σωματίδιο συμπεριφέρεται ως ηλεκτρικό δίπολο και αποκτά μια δυναμική ενέργεια. Στην πράξη κάθε δέσμη λέιζερ έχει ένα χωρικά μεταβαλλόμενο ηλεκτρικά πεδίο τόσο κατά μήκος του άξονα διάδοσης όσο και στο εγκάρσιο επίπεδο με αποτέλεσμα η δυναμική ενέργεια του σωματιδίου να μεταβάλλεται στο χώρο (ή σε μια πιο μαθηματική γλώσσα να έχει μια χωρική βαθμίδα). Το τελευταίο είναι απαραίτητο για να εμφανιστεί μια δύναμη που αντιστοιχεί σε αυτή τη δυναμική ενέργεια. Για αυτό το λόγο στη βιβλιογραφία η διπολική δύναμη είναι γνωστή και ως δύναμη βαθμίδας (gradient force). Το μέτρο αυτής της δύναμης εξαρτάται από το πόσο ισχυρή είναι η βαθμίδα της δυναμικής ενέργειας. Όταν εστιάζουμε ισχυρά μια δέσμη την περιορίζουμε στο χώρο με αποτέλεσμα η βαθμίδα της έντασής της και κατά συνέπεια της δυναμικής ενέργειας να είναι πολύ μεγάλη και η διπολική δύναμη να είναι ισχυρή. Η κατεύθυνση της διπολικής δύναμης εξαρτάται από τη σχέση του δείχτη διάθλασης του υλικού του σωματιδίου ως προς αυτόν του μέσου μέσα στο οποίο εμβαπτίζουμε το σωματίδιο. Αν το σωματίδιο έχει υψηλότερο δείχτη διάθλασης τότε κατευθύνεται προς τις περιοχές που η ένταση της δέσμης είναι ισχυρή. Στην αντίθετη περίπτωση κατευθύνεται προς τις περιοχές που η ένταση είναι ασθενής. Στις Εικ. 3 δίνουμε την μεταβολή της έντασης μιας δέσμης λέιζερ στο χώρο.

Εικόνα 3: Η ένταση μιας συμβατικής δέσμης λέιζερ περιγράφεται από μια Γκαουσιανή χωρική συνάρτηση, οποία περιλαμβάνει τρεις βασικές παραμέτρους: τη μέγιστη ένταση Ιο που έχουν όλα τα σημεία της δέσμης που βρίσκονται πάνω στον άξονα διάδοσης/συμμετρίας της (x = y = 0), το εύρος δέσμης (beam waist) w0 που αντιστοιχεί στην απόσταση από τον άξονα διάδοσης στην οποία η ένταση λαμβάνει την τιμή Ιο/e2 και το μήκος Rayleigh zR (Rayleigh range/length) που αντιστοιχεί στην απόσταση κατά μήκος του άξονα διάδοσης όπου η ένταση της δέσμης πέφτει στο μισό της μέγιστης τιμής. Οι δύο τελευταίοι παράμετροι συνδέονται μεταξύ τους και με το μήκος κύματος λ με τη σχέση: zR= πw20/λ.
Οι οπτικές λαβίδες μπορούν να παγιδεύουν σωματίδια με διαστάσεις που κυμαίνονται από αυτήν ενός ατόμου έως και μερικά εκατομμυριοστά του μέτρου. Οι δυνάμεις που ασκούνται από τις οπτικές λαβίδες στα σωματίδια έχουν μέτρο που μπορεί να υπερβεί τα 100 pN (10-12 Ν) (Litvinov, 2002). Για να έχουμε μια αίσθηση, το μέγεθος αυτής της δύναμης είναι περίπου εκατό φορές μεγαλύτερο από το βάρος ενός βακτηρίου
Ο ΔΡΟΜΟΣ ΠΡΟΣ ΤΙΣ ΟΠΤΙΚΕΣ ΛΑΒΙΔΕΣ
Οι οπτικές λαβίδες έλκουν την καταγωγή τους από ένα ιστορικό πείραμα που πραγματοποιήθηκε το 1970 από τον Αshkin στα Bell Labs στις ΗΠΑ (Ashkin, 1970). Η αιτία που οδήγησε τον Ashkin στην εκτέλεσή του ήταν, απλά και μόνο, η περιέργεια για ένα αποτέλεσμα που είχε ανακοινώσει κάποιος διδακτορικός φοιτητής σε ένα συνέδριο. Στο πείραμα αυτό ο Ashkin πέτυχε την μετακίνηση μικροσκοπικών σφαιριδίων από καουτσούκ με τη βοήθεια μιας δέσμης λέιζερ. Οι διαστάσεις των σφαιριδίων ήταν περίπου είκοσι εκατομμυριοστά του μέτρου (20 μm). Στο πείραμα αυτό η δύναμη από τη δέσμη του λέιζερ εξισορρόπησε την επίδραση της βαρύτητας πάνω στα σφαιρίδια. Το φαινόμενο αυτό είναι γνωστό στη βιβλιογραφία ως οπτική ανύψωση (optical levitation). Ενδεικτικό της σημασίας αυτού του πειράματος είναι οι εκατοντάδες αναφορές που έχει λάβει στη βιβλιογραφία το άρθρο στο οποίο αναφέρθηκαν τα αποτελέσματά του. Από την ερευνητική ομάδα του Ashkin έγιναν και τα πρώτα βιολογικά πειράματα με οπτικές λαβίδες που περιλάμβαναν τη σύλληψη βακτηρίων και μικρού αριθμού ιών σε ποικιλίες καπνού καθώς και τον χειρισμό της κίνησης κυττάρων και κυτταρικών οργανιδίων.
οπτική λαβίδα εφευρέθηκε το 1980 από τον Ashkin και τον S. Chu όταν κατόρθωσαν να μετακινήσουν, και ταυτόχρονα, να παγιδεύσουν σε μια μικρή περιοχή, μικρά διηλεκτρικά σφαιρίδια (Ashkin, 1986). Ο Chu λίγα χρόνια μετά θα χρησιμοποιήσει τις ίδιες τεχνικές για να παγιδεύσει άτομα. Για αυτό το επίτευγμα o Chu θα μοιραστεί το βραβείο Νόμπελ φυσικής το 1997.
Στα σύγχρονα πειράματα για να μπορούμε να εξουδετερώσουμε την επίδραση του βάρους χρησιμοποιούμε υγρά μέσα (π.χ. νερό), στα οποία τα εμβαπτιζόμενα σωμάτια αιωρούνται λόγω της επίδρασης της άνωσης. Η χρήση του νερού προστατεύει τα σωμάτια, ιδιαίτερα αν αυτά είναι τμήματα βιολογικών ιστών, από καταστροφές τις οποίες μπορεί να προκαλέσει η υπερθέρμανση από την ακτινοβολία της δέσμης λέιζερ.
Εν γένει οι οπτικές λαβίδες βασίζονται στην χρήση του αντικειμενικού φακού ενός μικροσκοπίου. Ο φακός εστιάζει τη δέσμη και μας δίνει μια ισχυρή δύναμη στην εστία του η οποία μπορεί να παγιδεύσει το σωματίδιο σε αυτήν την περιοχή. Εντούτοις η ισχυρή εστίαση περιορίζεται από το λεγόμενο όριο περίθλασης (diffraction limit), δηλαδή από την αδυναμία του μικροσκοπίου να επιτύχει ανάλυση δύο σημείων των οποίων η απόσταση είναι μικρότερη από το ήμισυ του μήκους κύματος. Ως αποτέλεσμα το μέγεθος της περιοχής εστίασης είναι της τάξης μεγέθους του μήκους κύματος δηλαδή μερικές εκατοντάδες νανόμετρα. Αυτό περιορίζει την ποιότητα και ακρίβεια της παγίδευσης. Είναι αξιοσημείωτο το γεγονός ότι η ίδια δέσμη λέιζερ που χρησιμοποιούμε για την παγίδευση των σωματιδίων εισάγεται ταυτόχρονα σε ένα συμβατικό οπτικό μικροσκόπιο ώστε να μπορούμε να παρατηρήσουμε την κίνηση των σωματιδίων.
Mία ακτίνα λέιζερ ισχύος περίπου 1 mW είναι αρκετή για την παγίδευση ενός διαφανούς σωματιδίου, σαν αυτά που απαντώνται στα βιολογικά δείγματα. Γενικά μπορούμε να παγιδεύουμε μια ποικιλία σωματιδίων μεταβάλλοντας απλά το μήκος κύματος. Στις περισσότερες οπτικές λαβίδες χρησιμοποιούμε λέιζερ Nd:YAG (είδος ερυθρού πολύτιμου λίθου με προσμίξεις ιόντων νεοδυμίου) επειδή έχουν πολύ καλή ευστάθεια δέσμης και, φυσικά, λόγω της χαμηλής απορρόφησης της ακτινοβολίας μήκους κύματος 1064 nm (στο εγγύς υπέρυθρο) από τα βιολογικά υλικά.
Στην περίπτωση που το μέγεθος ενός σωματιδίου είναι αρκετά μεγαλύτερο από το μήκος κύματος της δέσμης λέιζερ, το θεωρητικό όριο του μεγέθους των δυνάμεων που ασκεί μια οπτική λαβίδα (μήκους κύματος λ) σε ένα σωματίδιο καθορίζεται από την ορμή h/λ ανά φωτόνιο κατά την απορρόφησή του από το σωματίδιο ή 2h/λ κατά την ανάκλασή του. Στην πράξη, εντούτοις, το όριο είναι περίπου 0,2-0,5 h/λ ενώ στην περίπτωση ενός βακτηρίου με χαμηλό δείκτη διάθλασης μπορεί να φτάσει και την τιμή 0,01 h/λ ανά φωτόνιο. Για να έχουμε μια ποσοτική εκτίμηση της δύναμης ας υποθέσουμε πως διαθέτουμε μια δέσμη λέιζερ ισχύος P και συχνότητας f. Αυτό σημαίνει πως ο αριθμός των φωτονίων που μας παρέχει η δέσμη ανά δευτερόλεπτο είναι ίσος με P/hf. H ορμή που μεταφέρει κάθε ένα από αυτά τα φωτόνια είναι ίση με hλ ή hf/c (όπου c η ταχύτητα του φωτός). Αν υποθέσουμε πως αυτά τα φωτόνια ανακλώνται πάνω σε ένα σωματίδιο τότε επιφέρουν σε αυτό μια μεταβολή της ορμής ίση με 2 hf/c. Συνεπώς για τη δύναμη που ασκείται πάνω στο σωματίδιο θα ισχύει:
2(P/hf)(hf/c) = 2P/c,
Όπως είναι εμφανές η δύναμη που ασκεί μια οπτική λαβίδα σχετίζεται με τη διαθέσιμη ισχύ. Για παράδειγμα για διαθέσιμη ισχύ 1 mW η δύναμη είναι της τάξης των 7 pN (10-12 N). Φυσικά σε ένα πείραμα δεν μπορούμε να χρησιμοποιήσουμε πολύ υψηλή ισχύ, ιδιαίτερα στην περίπτωση που χρησιμοποιούμε βιολογικά σωματίδια, καθώς αυτό επιφέρει υπερθέρμανση των σωματιδίων και πιθανή καταστροφή τους.
ΟΙ ΟΠΤΙΚΕΣ ΛΑΒΙΔΕΣ ΣΤΗ ΒΙΟΛΟΓΙΑ
Οι οπτικές λαβίδες έχουν μεγάλες βιολογικές εφαρμογές που αφορούν στην παγίδευση, κίνηση και τοποθέτηση μια μεγάλης ποικιλίας μεμονωμένων κυττάρων και υποκυτταρικών σωματιδίων. Η εφαρμογή των οπτικών λαβίδων στην κυτταρική βιολογία είναι εφικτή γιατί τα περισσότερα κύτταρα, παράσιτα και άλλοι μικροοργανισμοί είναι διαφανή στις ακτινοβολίες του ορατού φάσματος.
Στην περίπτωση ενός διπόλου η δυναμική ενέργεια U είναι ανάλογη της έντασης η οποία για μια Γκαουσιανή δέσμη λέιζερ έχει κυλινδρική συμμετρία και δίνεται από τη σχέση:
(1) 
Είναι προφανές πως από μια τέτοια δυναμική ενέργεια θα προκύψουν δύο συνιστώσες για την διπολική δύναμη. Η μία έχει αξονική διεύθυνση και κοντά στην εστία (z = 0, ) δίνεται από τη σχέση:
(2) 
Η άλλη έχει αξονική διεύθυνση και κοντά στην εστία δίνεται από τη σχέση:
(3) 
Είναι προφανές πως οι δύο δυνάμεις έχουν το χαρακτήρα δύναμης επαναφοράς ελατηρίου με αποτέλεσμα το σωματίδιο να τείνει να ισορροπήσει κοντά στην εστία (όταν το σωματίδιο έχει υψηλότερο δείχτη διάθλασης από το μέσο στο οποίο είναι εμβαπτισμένο). Από τις παραπάνω σχέσεις είναι επίσης προφανές πως όταν εστιάζουμε ισχυρά τη δέσμη οι τιμές των και ελαττώνονται δραστικά και αυτό οδηγεί σε μεγαλύτερες τιμές των σταθερών επαναφοράς άρα και ισχυρότερη παγίδευση.
Η περίοδος μετά την ανακάλυψη της οπτικής λαβίδας χαρακτηρίστηκε από μια έντονη ερευνητική δραστηριότητα. Το 1989 η ομάδα του S. M. Block έκανε τις πρώτες ακριβείς μετρήσεις της ελαστικότητας των μαστίγιων των βακτηρίων (Block, 1989) με τη βοήθεια οπτικών λαβίδων. Αυτές οι μετρήσεις άνοιξαν τον δρόμο για την χρήση των οπτικών λαβίδων ως μεταδοτών δυνάμεων σε κυτταρικό επίπεδο.
Το πείραμα της ομάδας του Block ακολούθησαν μια σειρά άλλα ενδιαφέροντα πειράματα. Στο Πανεπιστήμιο του Χάρβαρντ εκτελέστηκαν νέα πειράματα για τη μέτρηση της ελαστικότητας του μαστίγιου των βακτηρίων. Στο Βασιλικό Κολλέγιο (King’s College) του Πανεπιστημίου του Λονδίνου οι οπτικές λαβίδες αξιοποιήθηκαν για να μετρηθούν οι δυνάμεις που ασκούνται από μεμονωμένες μυϊκές ίνες. Στη Γλασκόβη έχουν γίνει προσπάθειες χρήσης οπτικών λαβίδων για τη μελέτη και απομόνωση παρασίτων στο νερό. Στη Γκρενόμπλ τις χρησιμοποίησαν στο χειρισμό μαγνητικών σωματιδίων ενώ στο Πρίνστον (Princeton) έχουν μετρηθεί οι ελαστικές ιδιότητες των ελίκων του DNA (Wang, 1997). Τέλος στο Πολυτεχνείο του Worcester στη Μασαχουσέτη έκοψαν με τη βοήθεια λέιζερ ένα κύτταρο και στη συνέχεια, με τη βοήθεια μιας λαβίδας, εμφύτευσαν ένα απλό βακτήριο μέσα σε αυτό (Grier, 2003). Οι βιολογικές εφαρμογές των οπτικών λαβίδων περιλαμβάνουν ακόμη την μέτρηση της αντίστασης της ουράς των βακτηρίων, την μέτρηση των δυνάμεων που ασκούνται από πρωτεΐνες, τη μέτρηση της διάτασης των μορίων του DNA και την κατασκευή ενός οπτικού ψαλιδιού για την διάσχιση κυτταρικών σωματιδίων (Bayles, 1993).
Ιδιαίτερης σημασίας είναι η χρήση των οπτικών λαβίδων στην κατά βούληση ανάπτυξη των νευρώνων όπου η μηχανική παραμόρφωση της κυτταρικής μεμβράνης επηρεάζει εμφανώς την ανάπτυξη και την κινητικότητα των κυττάρων. Σε αυτήν την περίπτωση απαιτείται ακριβής και ενδελεχής μελέτη των μηχανικών ιδιοτήτων των κυττάρων. Επίσης, μεγάλης σημασίας είναι η ανάπτυξη της οπτικής χρωματογραφίας (optical chromatography) που αφορά τον διαχωρισμό διαφορετικών σωματιδίων που είναι εμβαπτισμένα σε κάποιο ρευστό μέσο καθώς και της οπτορευστολογίας (optofluidics) η οποία μελετά την παγίδευση σωματιδίων από οπτικές λαβίδες και την μεταφορά και διοχέτευσή τους στα κυτταρικά ρευστά (Jones, 2016).
Οι οπτικές λαβίδες έχουν αποδειχθεί ιδανικό εργαλείο για τη μελέτη της δυναμικής των λεγόμενων μοριακών μηχανών (molecular machines), ένα παράδειγμα των οποίων είναι το μόριο της μυοσίνης. Μια μοριακή μηχανή λειτουργεί χάρη στη χημική ενέργεια που απελευθερώνεται από υδρόλυση τριφωσφορικής αδενοσίνης (ATP), η οποία τελικά μετασχηματίζεται σε μια κίνηση των νημάτων ακτίνης και μυοσίνης που καθορίζει τη συστολή μυών. Τα πρώτα πειράματα προς αυτήν την κατεύθυνση πραγματοποιήθηκαν στα μέσα της δεκαετίας του 1990 (Jones, 2016).
Είναι σημαντικό να κατανοηθεί ότι με τις οπτικές λαβίδες η μελέτη των βιολογικών υλικών περνά σε ένα διαφορετικό ποιοτικό επίπεδο. Μέχρι τα μέσα της δεκαετίας του ‘80 η γνώση μας για τις μηχανικές ιδιότητες των βιολογικών υλικών προερχόταν από μετρήσεις πάνω σε ορισμένες ποσότητες υλικού. Στη συνέχεια οι ιδιότητες των μεμονωμένων μορίων εξάγονταν από μοντελοποίηση και χρήση στατιστικών μεθόδων. Σήμερα έχουμε τη δυνατότητα να εξετάζουμε αυτές τις ιδιότητες και να εκτελούμε μετρήσεις πάνω σε μεμονωμένα μόρια, οπότε αναδεικνύουμε φαινόμενα και ιδιότητες που πιθανόν να «χάνονταν» από μια στατιστική αντιμετώπιση, όπως οι ιδιαίτερες απόψεις των πολιτών χάνονται πίσω από τους «μέσους όρους» των δημοσκοπήσεων.
ΟΙ ΟΠΤΙΚΕΣ ΛΑΒΙΔΕΣ ΣΤΗ ΜΙΚΡΟΜΗΧΑΝΙΚΗ
Οι οπτικές λαβίδες αποτελούν αναπόσπαστο εργαλείο της μικρο- και νανομηχανικής. Η χρήση των οπτικών λαβίδων σε μικροσκοπικές μηχανές απέκτησε νέες προοπτικές όταν χρησιμοποιήθηκαν σε αυτές λέιζερ με οπτικούς στροβίλους (optical vortex beams). Πρόκειται για δέσμες λέιζερ των οποίων τα φωτόνια φέρουν, ως προς τον άξονα διάδοσης της δέσμης, εκτός από ορμή και στροφορμή (Allen, 1992). Η στροφορμή μάλιστα κάθε φωτονίου είναι ίση lℏ όπου l=±1, ±2, … και η ανηγμένη σταθερά του Planck (ℏ=h/2π). Οι δέσμες αυτές είναι ικανές όχι μόνο να μετακινήσουν σωματίδια αλλά και να τα περιστρέψουν. Το πλεονέκτημα αυτών των δεσμών είναι ότι μπορούν να λειτουργούν σε χαμηλή ισχύ και συνεπώς δεν κινδυνεύουν οι μικροοργανισμοί από καταστροφή. Το φαινόμενο της περιστροφής σωματιδίων με χρήση τέτοιων δεσμών παρατηρήθηκε, για πρώτη φορά, το 1995 σε μικρές σφαίρες από γυαλί και τεφλόν εμβαπτισμένες σε νερό ή αλκοολικό διάλυμα (He, 1995).

Εικόνα 4: Είκοσι έξι σφαιρίδια από πολυστυρένιο με διάμετρο τρία εκατομμυριοστά του μέτρου (3 μm), παγιδευμένα σε μορφή «κολιέ» με τη βοήθεια ενός οπτικού στροβίλου. Ευγενική προσφορά του καθηγητή K. Dholakia επικεφαλής του Optical Manipulation Group του Πανεπιστήμιου St. Andrew’s του Ηνωμένου Βασίλειου.
Οι οπτικές λαβίδες με οπτικούς στροβίλους προσφέρουν το ιδανικό περιβάλλον για τη μελέτη των διαφόρων τύπων στροφορμής λόγω των περίπλοκων ροπών που ασκούν. Οι ροπές αυτές είναι αρκετά ισχυρές ώστε να προκαλέσουν την περιστροφή μικροσκοπικών σωματιδίων. Το πρώτο τέτοιο επίτευγμα ήταν η δημιουργία ενός οπτικού κλειδιού σύσφιξης (optical spanner). Σε αυτό το πείραμα σωματίδια από τεφλόν ακτινοβολήθηκαν από έναν κυκλικά πολωμένο οπτικό στρόβιλο και τέθηκαν σε περιστροφή (Simpson, 1997). Εξαιρετικά ενδιαφέρον, από την πλευρά της φυσικής, είναι το γεγονός πως η κυκλική πόλωση, ανάλογα τη φορά της (δεξιόστροφη ή αριστερόστροφη) συνεισέφερε, ανά φωτόνιο, μια πρόσθετη μονάδα στροφορμής ±ℏ στα σωματίδια. Δηλαδή αν ο οπτικός στρόβιλος ήταν δεξιόστροφα (αριστερόστροφα) πολωμένος τα σωματίδια από τεφλόν αποκτούσαν μια στροφορμή (l±1)h- ανά φωτόνιο μετά την αλληλεπίδραση με τη δέσμη.
Από τους πρωτοπόρους σε σχετικά πειράματα ήταν η ομάδα της H. Rubinsztein-Dunlop του Πανεπιστημίου του Queensland στην Αυστραλία. Σε ένα από αυτά τα πειράματα παρουσιάστηκε μια μοντέρνα εκδοχή του περίφημου πειράματος του Beth (Beth, 1936) o οποίος είχε μετρήσει τη ροπή που ασκείται σε ένα μικρό πλακίδιο από χαλαζία όταν αυτό ακτινοβοληθεί από κυκλικά πολωμένο φως (Friese 1998). Σε μια σειρά άλλων πειραμάτων, οι P. Galajda και P. Ormos της Ουγγρικής Ακαδημίας Επιστημών στο Szeged (Galajda, 2001) και η ομάδα του E. Higurashi στο οπτοηλεκτρονικό εργαστήριο της ΝΤΤ στην Ιαπωνία, απέδειξαν ότι η ροπή που ασκεί η ακτινοβολία μπορεί εύκολα να κάνει τα μόρια να συμπεριφέρονται σαν λεπίδες ανεμιστήρα (Higurashi, 1999). Ανάλογες τεχνικές έχουν χρησιμοποιηθεί στην περιστροφή και στοίχιση των χρωματοσωμάτων σε κινέζικα χάμστερ αλλά και σε ομάδες ραβδόμορφων σωματιδίων (Paterson, 2001).
Το 2018 παρουσιάστηκε μια θεαματική εφαρμογή οπτικών λαβίδων που μετέτρεψε σε πραγματικότητα μια πρόβλεψη που έκανε ο Feynman πριν από εξήντα χρόνια (Feynman, 2011). Ο Feynman είχε προτείνει μια διάταξη, γνωστή ως γρανάζι του Feynman (Feynman’s ratchet). Πρόκειται για μια υποθετική μικροσκοπική μηχανή θερμότητας που μετατρέπει τις θερμικές διακυμάνσεις σε ωφέλιμο μηχανικό έργο όταν έρχεται σε θερμική επαφή με δύο δεξαμενές θερμότητας σε διαφορετικές θερμοκρασίες. Αυτή η μηχανή, σύμφωνα με τον Feynman, αποτελείται από ένα σετ μικροσκοπικών λεπίδων που συνδέονται με το ένα άκρο ενός άξονα. Αυτές οι λεπίδες βομβαρδίζονται συνεχώς από τα μόρια ενός αερίου που περικλείεται σε ένα δοχείο. Το άλλο άκρο του άξονα συνδέεται με γρανάζι και μπορεί συνεπώς να περιστραφεί μόνο κατά μία φορά. Η πειραματική εφαρμογή αυτής της μικρομηχανής κατέστη δυνατή έπειτα από μια συνεργασία μεταξύ Αμερικανών και Κινέζων ερευνητών σε ένα πείραμα όπου έγινε χρήση 19 οπτικών λαβίδων (Bang, 2018).
ΜΟΝΤΕΛΑ ΘΕΡΜΟΔΥΝΑΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΜΕΛΕΤΗ ΘΕΜΕΛΙΑΚΩΝ ΑΡΧΩΝ ΤΗΣ ΦΥΣΙΚΗΣ.
Ο πιο «παράξενος» νόμος στη φυσική είναι ο διαβόητος Δεύτερος Θερμοδυναμικός Νόμος καθώς δεν έχει, μέχρι τώρα, διαψευσθεί και κυρίως καμία αναθεώρηση της φυσικής, δεν τον έχει αγγίξει. Σύμφωνα με αυτόν το νόμο κάθε απομονωμένο θερμοδυναμικό σύστημα χαρακτηρίζεται από μια ποσότητα την εντροπία (ουσιαστικά ένα μέτρο της αταξίας του συστήματος) η οποία σε όλες τις αυθόρμητες μεταβολές του συστήματος δεν μπορεί να μειώνεται καθώς αυτό φτάνει σε μια κατάσταση θερμοδυναμικής ισορροπίας όπου η εντροπία του γίνεται μέγιστη.
Οι οπτικές λαβίδες, χρησιμοποιήθηκαν σε ένα πείραμα με κολλοειδή σωμάτια στο οποίο παρατηρήθηκαν αποκλίσεις από το Δεύτερο Νόμο της Θερμοδυναμικής κάτω από συγκεκριμένες συνθήκες. Ο D. Evans από το Εθνικό Πανεπιστήμιο της Αυστραλίας στην Καμπέρα με τους συνεργάτες του έδειξαν ότι σε ένα μικροσκοπικό σύστημα και σε μικρό χρονικό διάστημα η εντροπία μπορεί να ελαττωθεί, αντί να αυξηθεί (Wang, 2002). Αυτό το συμπέρασμα έχει σημαντικές συνέπειες στη λειτουργία των νανομηχανών. Ας δούμε το γιατί.
Από τη θερμοδυναμική γνωρίζουμε πως η συνεχής μείωση του μεγέθους των μηχανών έχει ένα θεμελιώδες όριο: όταν το έργο το οποίο παράγεται σε κάθε κύκλο μηχανής είναι συγκρίσιμο με την ενέργεια των θερμικών διακυμάνσεων του περιβάλλοντος, τότε μια τέτοια μηχανή, σε μικρές χρονικές κλίμακες, μπορεί να αντιστρέψει τη λειτουργία της. Αυτό πρακτικά σημαίνει πως θερμότητα από το περιβάλλον, μπορεί να μετατραπεί σε χρήσιμο μηχανικό έργο, κάνοντας την νανομηχανή να λειτουργεί αντίστροφα. Οι επιστήμονες δεν είχαν δώσει προσοχή σε αυτό το ενδεχόμενο. Μια πιθανή εξήγηση ήταν η απουσία ποσοτικής περιγραφής της παραγωγής εντροπίας σε μηχανές τόσο μικρών διαστάσεων. Το μόνο που είχαμε στα χέρια μας ήταν ο Δεύτερος Θερμοδυναμικός Νόμος, ο οποίος, ουσιαστικά αφορά τη θερμοδυναμική μεγάλων συστημάτων, για μεγάλους χρόνους, όπου αναγκαστικά έχουμε αύξηση της εντροπίας. Το πρόβλημα αυτό λύθηκε το 1993 όταν διατυπώθηκε από τους Evans και Searles το Θεώρημα των Διακυμάνσεων το οποίο προβλέπει μια ποσοτική περιγραφή των παραβιάσεων του Δεύτερου Θερμοδυναμικού Νόμου (Evans, 1994).
Οι οπτικές λαβίδες έχουν συμβάλλει στην πειραματική επαλήθευση όλων των περιορισμών που σχετίζονται με τη λειτουργία νανομηχανών. Το 2012, οι V. Blickle και C. Bechinger κατάφεραν να κατασκευάσουν μια μικροσκοπική μηχανή παγιδεύοντας ένα κολλοειδές σωματίδιο με τη βοήθεια οπτικών λαβίδων (Blickle, 2012). Αυτός κινητήρας λειτούργησε στην πραγματικότητα ακολουθώντας μια μικροσκοπική εκδοχή του γνωστού θερμοδυναμικού κύκλου Stirling που συνίσταται από δύο ισόθερμες και δύο ισόχωρες αντιστρεπτές διαδικασίες.
Η δυναμική των παγιδευμένων σωματιδίων μέσα στις οπτικές λαβίδες προκύπτει από έναν συνδυασμό μιας ντετερμινιστικής κίνηση που καθορίζεται από τις δυνάμεις που ασκούνται από την οπτική λαβίδα και μιας χαοτικής κίνησης Brown που επιβάλλεται από τις τυχαίες συγκρούσεις των σωματιδίων με τα μόρια του μέσου στο οποίο αυτά εμβαπτίζονται. Η συνύπαρξη αυτών των δύο διαφορετικού χαρακτήρα κινήσεων καθιστά τις οπτικές λαβίδες μια ιδανική πλατφόρμα για την εξερεύνηση των θεμελιωδών φαινομένων της στατιστικής φυσικής. Μεταξύ αυτών των φαινομένων είναι οι ρυθμοί Kramers, ο στοχαστικός συντονισμός, η κρυστάλλωση μορίων, τα τυχαία δυναμικά και η ακανόνιστη διάχυση.
Οι ρυθμοί Kramers σχετίζονται με τη δυναμική με την οποία αναπτύσσονται θερμικά επαγόμενες μεταβάσεις που απαντώνται στη φυσική, τη χημεία και τη βιολογία. Το φαινόμενο του στοχαστικού συντονισμού εμφανίζεται σε ορισμένα συστήματα όταν η παρουσία θορύβου μπορεί να επιταχύνει τον ρυθμό με τον οποίο ένα σύστημα αποκρίνεται σε ένα εξωτερικό περιοδικό σήμα. Τα τυχαία δυναμικά, δηλαδή εκείνα στα οποία δεν υπάρχει περιοδικότητα στο δυναμικό τοπίο, είναι ένας βασικός μηχανισμός για την κατανόηση φαινομένων που ξεκινούν από την ακανόνιστη διάχυση των μορίων εντός του κυτταροπλάσματος έως την εμφάνιση μιας κίνησης τύπου Brown σε αστέρια μέσα στους γαλαξίες.
Οι οπτικές λαβίδες έχουν επίσης συμβάλει στην έρευνα και μελέτη των επιφανειακών πλασμονίων και των εφαρμογών τους. Τα επιφανειακά πλασμόνια είναι τα κβάντα των συλλογικών ταλαντώσεων στο πλάσμα, δηλαδή των ελεύθερων ηλεκτρόνιων των μετάλλων και αναπτύσσονται είτε σε λείες διεπιφάνειες μεταξύ διηλεκτρικών υλικών και μετάλλων ή σε χωρικά οριοθετημένες γεωμετρικές δομές όπως τα νανοσωματίδια. Οι πολύ μικρές διαστάσεις αυτών των περιοχών παρέχουν ένα ευνοϊκό περιβάλλον για την ανάπτυξη πλασμονίων, που χαρακτηρίζονται από ισχυρά ηλεκτρομαγνητικά πεδία εντοπισμένα σε περιοχές του χώρου με διαστάσεις μικρότερες από τις όριο περίθλασης στο οποίο έχουμε αναφερθεί προηγουμένως. Σε αυτήν την περίπτωση, τα πλασμόνια αλληλεπιδρούν ισχυρά με νανοσωματίδια, και κατά συνέπεια μπορούν να χρησιμοποιηθούν για την κατασκευή οπτικών λαβίδων.
ΟΙ ΟΠΤΙΚΕΣ ΛΑΒΙΔΕΣ ΣΤΑ ΚΟΛΛΟΕΙΔΗ ΣΥΣΤΗΜΑΤΑ ΚΑΙ ΣΤΗΝ ΧΗΜΕΙΑ
Τα κολλοειδή είναι συστήματα τα οποία αποτελούνται από σωματίδια τα μεγέθη των οποίων κυμαίνονται από ένα νανόμετρο (10-9 m) έως μερικά μικρόμετρα (10-6 m) και είναι διασκορπισμένα σε ένα μέσο ξενιστή που μπορεί να είναι υγρό ή αέριο. Η δυναμική των κολλοειδών συστημάτων καθορίζεται κυρίως από την κίνηση Brown. Σε αυτά τα συστήματα αναδύονται ενδιαφέρουσες υδροδυναμικές και ηλεκτρομαγνητικές αλληλεπιδράσεις που μπορούν να οδηγήσουν τα σωματίδια στο σχηματισμό εξαιρετικά περίπλοκων δομών.
Οι οπτικές λαβίδες έχουν αποδειχθεί, για άλλη μια φορά, ότι είναι το ιδανικό εργαλείο για τη μελέτη αυτών των φαινομένων. Τα πρώτα σχετικά πειράματα πραγματοποιήθηκαν στα τέλη της δεκαετίας του 1990 (Burns, 1990). Μεταξύ αυτών περιλαμβάνονται πειράματα στα οποία εκδηλώθηκαν πολύ ενδιαφέροντα φαινόμενα σε συνθήκες μακριά από τη θερμοδυναμική ισορροπία, όπως η εμφάνιση αυτοοργάνωσης με την αυθόρμητη ανάδυση απροσδόκητων σχηματισμών από κολλοειδή σωματίδια.
Μια σημαντική κατηγορία κολλοειδών συστημάτων είναι τα αεροζόλ. Σε ένα αεροζόλ διασκορπίζονται μικροσκοπικά στερεά και υγρά σωματίδια σε ένα αέριο. Η μελέτη των αεροζόλ έχει μεγάλη σημασία σε τομείς όπως η χημεία της ατμόσφαιρας και σε εφαρμογές όπως η βελτίωση της ποιότητας της καύσης στους κινητήρες. Με τη βοήθεια οπτικών λαβίδων μπορούμε να παγιδεύουμε αυτά τα συστήματα και να μελετήσουμε εκείνες τις χημικές και φυσικές ιδιότητές τους που σχετίζονται με τις επιπτώσεις τους στο περιβάλλον, όπως η σύνθεσή τους και το μέγεθος των σωματιδίων.
Οι οπτικές λαβίδες μπορούν να αξιοποιηθούν στο χειρισμό σταγονιδίων, κυστών και των μεμβράνων τους, και να οδηγήσουν ένα πλήθος από αυτά σε συσσωμάτωση. Μπορούμε έτσι να σχηματίσουμε μεγαλύτερα σταγονίδια και κύστες, ενώ ταυτόχρονα διασφαλίζουμε και την διασπορά των συστατικών τους. Αυτή η ικανότητα μετατρέπει πραγματικά τα σταγονίδια και τις κύστες σε «φορητά δοχεία» ικανά να αποθηκεύσουν εξαιρετικά μικρές ποσότητες (της τάξης του τρισεκατομμυριοστού του λίτρου, 10-9 ml) από επιθυμητά χημικά αντιδραστήρια. Ακόμα πιο αξιοσημείωτο είναι ότι οι οπτικές λαβίδες επιτρέπουν την παρατήρηση σε πραγματικό χρόνο αυτών των αντιδράσεων μέσω τεχνικών φασματοσκοπίας γεγονός που μας επιτρέπει να κατανοήσουμε σε βάθος το φαινόμενο της ανάμιξης διαφορετικών ουσιών. Με τη βοήθεια οπτικών λαβίδων έχει ανοίξει ο δρόμος για την ανάπτυξη της μικροχημείας (microchemistry).
Η δυνατότητα να χειριζόμαστε την κίνηση μεμονωμένων ατόμων με τη βοήθεια των οπτικών λαβίδων προοικονομεί τεκτονικές αλλαγές στη χημεία και συγκεκριμένα στη διαύγαση της δυναμικής των χημικών αντιδράσεων. Μέχρι σήμερα όσα γνωρίζουμε για αυτές προέρχονται από πειράματα που περιλαμβάνουν τεράστιους αριθμούς μορίων. Σε αυτήν την περίπτωση ο σχηματισμός των μορίων είναι αποτέλεσμα τυχαίων κρούσεων μεταξύ των ατόμων. Το αποτέλεσμα είναι να μας διαφεύγουν κρίσιμες λεπτομέρειες, όπως για παράδειγμα το κατά πόσο η δυναμική της χημικής αντίδρασης διαφέρει ανάλογα με τη διαφορετική κβαντική κατάσταση που βρίσκονται τα άτομα ή μόρια. Σήμερα, χάρη στις οπτικές λαβίδες, έχουμε στη διάθεσή μας τους κβαντικούς συναρμολογητές (quantum assemblers). Πρόκειται για διατάξεις που περιλαμβάνουν τις οπτικές λαβίδες που μας βοηθούν να συνθέσουμε ένα μόριο από διαφορετικά άτομα και τις οπτικές λαβίδες που μας βοηθούν να παγιδεύουμε τα εν λόγω άτομα. Μια τέτοια περίπτωση έχουμε πρόσφατα με τη σύνθεση ενός μεμονωμένου μορίου NaCs αφού πρώτα απομονώσαμε με δυο διαφορετικές οπτικές λαβίδες ένα άτομο νατρίου (Na) και ένα άτομο κεσίου (Cs) (Liu, 2018). Αμέσως μετά η ίδια ερευνητική ομάδα κατόρθωσε να τοποθετήσει το συντιθέμενο μόριο σε μια συγκεκριμένη εσωτερική κβαντική κατάσταση (Liu, 2019).
ΕΠΙΛΟΓΟΣ – ΟΙ ΠΡΟΟΠΤΙΚΈΣ ΤΩΝ ΟΠΤΙΚΩΝ ΛΑΒΙΔΩΝ
Το μέλλον των οπτικών λαβίδων διαγράφεται λαμπρό. Για παράδειγμα, στη βιομηχανία το ενδιαφέρον για την οργάνωση μίκρο- και νάνο- συστατικών σε μεγαλύτερες δομές πηγάζει από πολλές πλευρές όπως η κατασκευή νέων χημικών αισθητήρων και η συναρμολόγηση ηλεκτρομηχανικών συστημάτων με πολύ μικρές διαστάσεις. Ακόμη υπάρχουν σοβαρές προοπτικές εφαρμογών στη βιομηχανική όπως, για παράδειγμα, στην προσπάθεια ελέγχου της οργάνωσης των κυττάρων κατά την διάρκεια ανάπτυξης ιστών και οργάνων. Οι οπτικές λαβίδες αφήνουν μεγάλες υποσχέσεις για την χειρουργική σε επίπεδο κυττάρου σε εφαρμογές όπως, για παράδειγμα, η τροποποίηση των χρωμοσωμάτων ζωντανών κυττάρων. Σε μεγαλύτερη κλίμακα μπορούν να αποδειχτούν χρήσιμες στη συλλογή μεμονωμένων μικροβίων από ετερογενείς πληθυσμούς ενώ η ικανότητά τους να μετακινούν με ακρίβεια κύτταρα έχει οδηγήσει σε κλινικές εφαρμογές όπως η in vitro γονιμοποίηση. Τέλος, όπως βλέπουμε στην Εικ. 1, με τις οπτικές λαβίδες μπορούμε να χειριστούμε σωματίδια σε μια μεγάλη κλίμακα μεγεθών, από άτομα που συμπεριφέρονται κβαντικά έως και κύτταρα που συμπεριφέρονται κλασικά. Με αυτόν τον τρόπο οι οπτικές λαβίδες αναδεικνύονται σε ένα πολύ αποτελεσματικό εργαλείο το οποίο μας παρέχει τη δυνατότητα να ερευνήσουμε και να διαυγάσουμε το όριο ανάμεσα στον κλασικό και τον κβαντικό κόσμο. Και εδώ, τα επόμενα χρόνια, οι προσδοκίες είναι πολύ μεγάλες.
ΕΥΧΑΡΙΣΤΙΕΣ
Η κεντρική εικόνα του άρθρου αποτελεί καλλιτεχνική προσαρμογή της εικόνας από το άρθρο https://physics.aps.org/articles/v11/100. Η προσαρμογή έγινε από τον ζωγράφο Παναγιώτη (Τάκη) Βαρελά, μέλος του ΔΣ του Εθνικού Μουσείου Σύγχρονης Τέχνης (ως εκπρόσωπος του Επιμελητήριου Εικαστικών Τεχνών Ελλάδας). Η συντακτική επιτροπή του InS ευχαριστεί τον κ. Βαρελά για την προσφορά του. Η εικόνα αναπαριστά τον εφελκυσμό μονόκλωνου DNA προσαρτημένου σε δύο σφαιρίδια με χρήση ισάριθμων οπτικών λαβίδων.
ΒΙΒΛΙΟΓΡΑΦΙΑ
Allen L., Beijersbergen M. W., Spreeuw R. J. C., and Woerdman J. P., 1992. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, p. 8185. https://doi.org/10.1103/PhysRevA.45.8185
Ashkin Α., 1970. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 24, p. 156. https://doi.org/10.1103/PhysRevLett.24.156
Ashkin A., Dziedzic J. M., Bjorkholm J. M., and Chu S., 1986. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 11, p. 288. https://doi.org/10.1364/OL.11.000288
Bang J., Pan R., Hoang T. M., Ahn J., Jarzynski C., Quan H. T., and Li T., 2018. Experimental realization of Feynman’s ratchet. New J. Phys. 20, 103032. https://doi.org/10.1088/1367-2630/aae71f
Bayles C. J, Aist J. R., and Berns M. W., 1993. The mechanics of anaphase-B in A basidomycete as revealed by laser microbeam microsurgery. Exp. Mycology 17, p. 191. https://doi.org/10.1006/emyc.1993.1018
Beth R. A., 1936. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 50, p. 115. https://doi.org/10.1103/PhysRev.50.115
Blickle V. and Bechinger C., 2012. Realization of a micrometre-sized stochastic heat engine. Nature Phys. 8, p.143. https://doi.org/10.1038/nphys2163
Block S. M., Blair D. F., and Berg H. C., 1989. Compliance of bacterial flagella measured with optical tweezers. Nature 338, p. 514. https://doi.org/10.1038/338514a0
Burns M. M., Fournier J.-M., and Golovchenko J. A., 1990. Optical matter: crystallization and binding in intense optical fields. Science 249, p. 749. 10.1126/science.249.4970.749
Evans D. J. and Searle D. J., 1994. Equilibrium microstates which generate second law violating steady states. Phys. Rev. E 50, p.1645. https://doi.org/10.1103/PhysRevE.50.1645
Feynman R. P., Leighton R. B., and Sands M., 2011. The Feynman Lectures on Physics, The New Millennium Edition. V.I-46. https://www.feynmanlectures.caltech.edu/
Friese M. E. J., Nieminen T. A., Heckenberg N. R., and Rubinsztein-Dunlop H., 1998. Optical alignment and spinning of laser-trapped microscopic particles. Nature 394, p.348. https://doi.org/10.1038/28566
Galajda P. and P. Ormos P., 2001. Complex micromachines produced and driven by light. Appl. Phys. Lett. 78, p. 249. https://doi.org/10.1063/1.1339258
Grier D., 2003. A revolution in optical manipulation. Nature 424, p. 810. https://doi.org/10.1038/nature01935
He H., Friese M. E. J., Heckenberg N. R., and Rubinsztein-Dunlop H., 1995. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 75, p. 826. https://doi.org/10.1103/PhysRevLett.75.826
Higurashi E., Sawada R., and Ito T., 1999. Optically induced angular alignment of trapped birefringent micro-objects by linearly polarized light. Phys. Rev. E 59, p. 3676. https://doi.org/10.1103/PhysRevE.59.3676
Jones P. H., Maragό O., and Volpe G., 2016. Optical Tweezers: Principles and Applications. Cambridge, USA: Cambridge Universiy Press. https://www.cambridge.org/core/books/optical-tweezers/D2D5FD82066E9FF88284C89095A2CB60
Litvinov R. I., Shuman H., Bennett J. S., and Weisel J. W., 2002. Binding strength and activation state of single fibrinogen-integrin pairs on living cells. Proc. Natl. Acad. Sci. 99, p. 7426. https://doi.org/10.1073/pnas.112194999
Liu L. R., Hood J. D., Yu Y., Zhang J. T., Hutzler N. R., Rosenband T., and Ni K.-K., 2018. Building one molecule from a reservoir of atoms. Science 360, p. 900. https://science.sciencemag.org/content/360/6391/900
Liu L. R., Hood J. D., Yu Y., Zhang J. T., Wang K., Lin Y.-W., Rosenband T., and Ni K.-K., 2019. Molecular assembly of ground-state cooled single atoms. Phys. Rev. X 9, 021039. https://doi.org/10.1103/PhysRevX.9.021039
Paterson L., MacDonald M. P., Arlt J., Sibbett W., Bryant P. E., and Dholakia K., 2001. Controlled rotation of optically trapped microscopic particles. Science 292(5518), p. 912. 10.1126/science.1058591
Simpson N. B., Dholakia K., Allen L., and Padgett M. J., 1997. Mechanical equivalence of spin and orbital angular momentum of light: an optical spanner. Opt. Lett. 22, p. 52–54. https://doi.org/10.1364/OL.22.000052
Wang M. D., Hong Y., Landick R., Gelles J.and Block S. M., 1997. Stretching DNA with Optical Tweezers. Biophysical Journal 22, p. 1335. 10.1016/S0006-3495(97)78780-0
Wang G. M., Sevick E. M., Mittag E., Searles D. J., and Evans D. J., 2002. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev.
Lett. 89, 050601. https://doi.org/10.1103/PhysRevLett.89.050601






Καλησπέρα κύριε Λεμπέση. Είμαι μαθητής στο τμήμα Μοριακής Βιολογίας του Δημοκρίτειου Πανεπιστημίου Θράκης και μαζί με άλλους δύο συμφοιτητές μου συγγράφουμε μια εργασία στο θέμα των optical tweezers. Θα ήθελα να ζητήσω την άδειά σας για την χρήση του άρθρου σας καθώς και των εικόνων που χρησιμοποιήσατε στην δικιά μας παρουσίαση. Σας ευχαριστώ εκ των προτέρων.
Αγαπητέ Ηλία. Εξαιτίας ενός τεχνικού σφάλματος στην πλατφόρμα μας είδα το μήνυμα σας με ….4 χρόνια καθυστέρηση!!!!
Ασφαλώς και θα σας έδινα την άδεια. Σας ζητώ, έστω και πολύ εκ των υστέρων συγγνώμη για αυτό το … κομφούζιο