O Richard Feynman υπήρξε ένας φυσικός o οποίος συνδύασε με μοναδικό τρόπο την πρωτοποριακή έρευνα με την απαράμιλλη διδασκαλία που άφησε εποχή στα πανεπιστημιακά αμφιθέατρα. Σε αυτό το άρθρο εστιάζουμε σε μια λιγότερη γνωστή, στο ευρύτερο κοινό, πτυχή της ερευνητικής του δραστηριότητας που αφορά στους ηλεκτρονικούς υπολογιστές και τη διαδικασία του υπολογισμού η οποία άνοιξε το δρόμο σε μια επανάσταση: αυτή των κβαντικών υπολογιστών.
Ο Feynman είναι ένας επιστήμονας ιδιαίτερα γνωστός στο ελληνικό αναγνωστικό κοινό καθώς τις τελευταίες δεκαετίες έχουν μεταφραστεί πολλά από τα βιβλία του. Ανάμεσα σε αυτά και το βιβλίο με τίτλο «Διαλέξεις για του Υπολογιστές» (Feynman, 2006). Στις σελίδες αυτού του βιβλίου ο Feynman αφενός μεν, δίνει τη δική του, μοναδική, άποψη για όλα τα θέματα που αφορούν στα θεμέλια των υπολογιστών αφετέρου δε, ανοίγει σημαντικούς δρόμους για την εξέλιξη των υπολογιστών πολύ πέρα από τη εικόνα και αντίληψη που είχαμε για αυτούς μέχρι τις ημέρες μας.
Το ενδιαφέρον του Feynman για τους υπολογιστές χρονολογείται από τα χρόνια του Σχεδίου Μανχάταν και τον σχεδιασμό της ατομικής βόμβας. Στο κεφάλαιο με τον τίτλο «Λος Aλάμος εκ των ένδον», το οποίο έχει δημοσιευτεί στο βιβλίο «Σίγουρα θα αστειεύεστε κ. Φάινμαν», ο Feynman διηγείται τα γεγονότα που οδήγησαν στην τοποθέτησή του ως επικεφαλής της «Ομάδας ΙΒΜ» η οποία είχε υπό την ευθύνη της τον υπολογισμό της ενέργειας που εκλύεται κατά την διάρκεια της έκρηξης (Feynman, 2018). Είναι ενδεικτικό πως, ακόμη και τότε, αρκετά πριν από την έλευση ενός πραγματικού υπολογιστή, ο Feynman και η ομάδα του ανέπτυξαν τρόπους για να κάνουν παράλληλους υπολογισμούς για την λειτουργία και απόδοση της βόμβας.
Ο Richard P. Feynman γεννήθηκε στο Far Rockaway της Νέας Υόρκης το 1918. Πήρε το πτυχίο στη φυσική το 1939 από το Ινστιτούτο Τεχνολογίας της Μασαχουσέτης (ΜΙΤ) και το διδακτορικό του δίπλωμα από το Πανεπιστήμιο του Princeton το 1942. Σε νεαρή ηλικία έλαβε μέρος στο Πρόγραμμα Manhattan που αφορούσε στην κατασκευή της ατομικής βόμβας στη διάρκεια του Β! Παγκοσμίου Πολέμου. Δίδαξε στα Πανεπιστήμια Cornell και California Institute of Technology (Caltech). Το 1965 τιμήθηκε με το βραβείο Νόμπελ στη φυσική, μαζί με τους Sin-Itiro Tomonaga και Joulian Schwinger, για την εργασία του στην κβαντική ηλεκτροδυναμική. Διατύπωσε επίσης μια μαθηματική θεωρία η οποία εξηγούσε το φαινόμενο της ιδανικής ρευστότητας του υγρού ηλίου. Στη συνέχεια, μαζί με τον Murray Gell-Mann, επιτέλεσε θεμελιώδες έργο στον τομέα των ασθενών αλληλεπιδράσεων, όπως η διάσπαση βήτα. Εκτός από τα παραπάνω επιτεύγματα, ο Feynman εισήγαγε εντελώς νέες υπολογιστικές τεχνικές όπως τα πασίγνωστα πλέον διαγράμματα Feynman, τα οποία – ίσως περισσότερο από κάθε άλλο φορμαλισμό στη νεότερη επιστήμη – άλλαξαν τον τρόπο με τον οποίο αντιλαμβανόμαστε τις θεμελιώδεις φυσικές διαδικασίες και υπολογίζουμε τα φυσικά μεγέθη που τις χαρακτηρίζουν.
Ο Feynman υπήρξε ένας εξαίρετος δάσκαλος και γι’ αυτό τιμήθηκε με το Μετάλλιο Διδασκαλίας Oersted το 1972. Στην προσωπική του ζωή υπήρξε λάτρης των κρουστών, της ζωγραφικής, του χορού και του γυναικείου φύλου. Ασχολήθηκε με τις επισκευές ραδιοφώνων, την παραβίαση κλειδαριών και την αποκρυπτογράφηση της ιερογλυφικής γραφής των Μάγια. Στη δεκαετία του ’80 συμμετείχε στην επιτροπή διερεύνησης των αιτίων της πτώσης του διαστημικού λεωφορείου Challenger.
Σε φιλοσοφικό επίπεδο ο Feynman δεν ήταν παρά ένας ακόμη εκπρόσωπος, και μάλιστα «δογματικά» προσκολλημένος, του αγγλοσαξονικού θετικισμού, που απεχθανόταν τις συζητήσεις γύρω από τις φιλοσοφικές προεκτάσεις των επιτευγμάτων της φυσικής.
ΠΡΟΦΗΤΗΣ ΜΙΑΣ ΝΕΑΣ ΕΠΟΧΗΣ
Σε μια ιστορική ομιλία του με τίτλο There’s Plenty of Room at the Bottom, στο Ετήσιο Συνέδριο της American Physical Society στις 29 Δεκεμβρίου του 1959, στο Caltech, ο Feynman αναδεικνύεται σε προφήτη μιας επανάστασης στο χώρο της τεχνολογίας η οποία σήμερα βρίσκεται σε πλήρη εξέλιξη (Feynman, 2005). Σε αυτή την ομιλία ο Feynman μίλησε, εξήντα χρόνια πριν, για την δυνατότητα να γράψουμε μια ολόκληρη εγκυκλοπαίδεια, όπως η Britannica, πάνω στην κεφαλή μιας καρφίτσας και έθεσε τις βάσεις και την φυσική νομιμοποίηση της νανοτεχνολογίας, θεμελιώνοντας θεωρητικά τη δυνατότητα κατασκευής νανομηχανών. Στην ίδια ομιλία θα βρούμε μια εκτενή και ενδελεχή αναφορά στη δυνατότητα της δραστικής μείωσης του όγκου των υπολογιστών και της συρρίκνωσής του στο επίπεδο λίγων ατόμων.
Όμως τα ζητήματα τα οποία έθεσε ο Feynman δεν ήταν απλά ποσοτικά. Δεν αφορούσαν, δηλαδή, σε μια απλή αναγωγή μεγέθους. Αντίθετα, προοικονομούσαν επαναστατικές εξελίξεις και ριζικές μεταβολές. Ως επιστήμονας υψηλού επιπέδου, ο Feynman, προέβλεψε πολύ εύστοχα την κατεύθυνση των εξελίξεων ξεκινώντας από την εφαρμογή των υπολογιστών στην πράξη. Εάν οι υπολογιστές πρέπει συνεχώς να γίνονται ταχύτεροι και μικρότεροι σε μέγεθος, σύντομα θα φθάσουμε σε ένα σημείο όπου ακόμη και οι λογικές πύλες και τα υπόλοιπα βασικά εξαρτήματα θα έχουν το μέγεθος μερικών ατόμων. Εκεί όμως βρίσκεται το βασίλειο της κβαντικής φυσικής, της οποίας οι νόμοι διαφέρουν ριζικά από αυτούς της κλασικής φυσικής. Αυτό έχει ως αποτέλεσμα την πλήρη ανατροπή της αντίληψης μας για την λειτουργία των υπολογιστών. Με την ομιλία αυτή, καθώς και με τις ομιλίες του σε συνέδρια τη δεκαετία του 1980 και με τις διαλέξεις του, από το 1983 έως το 1986, στο Caltech, ο Feynman συνέγραψε, κατά κάποιον τρόπο, την «ουβερτούρα» μιας νέας εποχής, αυτής των κβαντικών υπολογιστών.
ΔΥΣΚΟΛΑ ΥΠΟΛΟΓΙΣΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ
Πέρα από τους περιορισμούς που θέτει η φύση, υπάρχουν και υπολογιστικά προβλήματα που έχουν θέσει, στην κυριολεξία, σε δοκιμασία τις ικανότητες των υπολογιστών. Ένα από τα πιο διάσημα προβλήματα αυτού του τύπου είναι η παραγοντοποίηση ενός μεγάλου αριθμού που αποτελεί γινόμενο δυο πρώτων αριθμών. Ο πολλαπλασιασμός δύο πρώτων αριθμών είναι εύκολο πρόβλημα αλλά το αντίστροφο είναι στην κυριολεξία ένας εφιάλτης. Ακριβώς για αυτό το λόγο αποτελεί τη βάση όλων των συστημάτων κρυπτογράφησης από την ασφάλεια των συναλλαγών στο Διαδίκτυο μέχρι τη μετάδοση κρατικών μυστικών. Η βάση αυτών των συστημάτων είναι το σύστημα RSA, από τα αρχικά γράμματα των επωνύμων των ερευνητών του ΜΙΤ, Rivest, Samir και Aldeman αντίστοιχα (Rivest 1979). H εκρηκτική υπολογιστική δυναμική των κβαντικών υπολογιστών είναι ο λόγος που τεχνολογικά μεγαθήρια, όπως η Google και η Intel, εταιρείες οπλικών συστημάτων καθώς και αμυντικές και άλλες κυβερνητικές υπηρεσίες έχουν στρέψει το ενδιαφέρον τους σε αυτούς. Αντίστοιχα πυρετώδεις είναι και οι ρυθμοί στην ακαδημαϊκή κοινότητα: μόνο το 2015, για παράδειγμα, τρία μεγάλα περιοδικά δημοσίευσαν πάνω από 3.000 επιστημονικές εργασίες που αναφέρουν τους όρους «κβαντική πληροφορική» ή «κβαντική πληροφορία».
Ο κβαντικός υπολογισμός είναι, μαζί με την κβαντική προσομοίωση, τα δύο απότοκα της προφητικής ομιλίας του R. Feynman στο συνέδριο με θέμα «Η φυσική του υπολογισμού» που διοργανώθηκε στο ΜΙΤ το 1981 (Feynman, 1982). Το επόμενο μεγάλο βήμα πραγματοποιήθηκε το 1985, στο Πανεπιστήμιο της Οξφόρδης, όταν ο φυσικός D. Deutsch απέδειξε πως οι κβαντικοί υπολογιστές μπορούν πράγματι να εκτελέσουν υπολογισμούς οι οποίοι είναι αδύνατον να εκτελεσθούν από κλασικούς υπολογιστές (Deutsch, 1985). Ο κβαντικός υπολογισμός ξεκίνησε ως ερευνητικό πεδίο το 1994, όταν ο μαθηματικός P. Shor, στα εργαστήρια Bell, απέδειξε πως ένας κβαντικός υπολογιστής θα μπορούσε να επιλύσει το πρόβλημα της παραγοντοποίησης ενός μεγάλου αριθμού ο οποίος είναι γινόμενο δυο πρώτων αριθμών (Shor, 1994). Η σημασία αυτού του επιτεύγματος γίνεται εμφανής αν αφήσουμε τους αριθμούς να μιλήσουν μόνοι τους. Το 1994 χρειάστηκαν οκτώ ολόκληροι μήνες, και περισσότεροι από 1000 υπολογιστές, ώστε το κρυπτογραφικό σύστημα RSA να επιτύχει την παραγοντοποίηση ενός αριθμού 129 ψηφίων. Αν είχαμε τη δυνατότητα να φτιάξουμε έναν κβαντικό υπολογιστή με την ίδια περίπου ταχύτητα, ο αλγόριθμός του Shore θα εκτελούσε αυτήν την αποστολή σε λιγότερο από 10 δευτερόλεπτα.
ΜΙΑ ΝΕΑ ΥΠΟΛΟΓΙΣΤΙΚΗ ΛΟΓΙΚΗ
Για να εξηγήσουμε τι είναι αυτό που κάνει τους κβαντικούς υπολογιστές τόσο διαφορετικούς από τους αντίστοιχους κλασικούς θα ξεκινήσουμε από τo θεμελιώδες στοιχείο της πληροφορίας, το ένα bit. Ένα bit είναι, στην πράξη, κάποιο φυσικό σύστημα, το οποίο μπορεί να βρεθεί σε δυο διαφορετικές διακριτές καταστάσεις που αναπαριστούν δύο λογικές τιμές: ναι ή όχι, αληθής ή ψευδής, ή, απλά 1 και 0. Για παράδειγμα στους σημερινούς υπολογιστές, η διαφορά δυναμικού ανάμεσα στους οπλισμούς ενός πυκνωτή αναπαριστά ένα bit πληροφορίας: φορτισμένος πυκνωτής αντιστοιχεί στο 1 και αφόρτιστος στο 0. Ένα bit πληροφορίας μπορεί να κωδικοποιηθεί σε οποιοδήποτε φυσικό σύστημα αρκεί αυτό να διαθέτει τουλάχιστον δύο διακριτές καταστάσεις. Αν όμως επιλέξουμε ως bit, για παράδειγμα, το ηλεκτρόνιο ενός ατόμου το οποίο, μέσω ενός φυσικού μηχανισμού (για παράδειγμα η αλληλεπίδραση του ατόμου με το φως μιας συσκευής λέιζερ) εξαναγκάζεται να «περιφέρεται» σε δύο «καθορισμένες τροχιές» γύρω από τον πυρήνα, τότε τα πράγματα αρχίζουν και γίνονται λίγο πιο περίπλοκα. Στην κβαντική μηχανική το ηλεκτρόνιο, έχει την πιθανότητα να βρεθεί τόσο σε μια από δύο διαφορετικές καταστάσεις («τροχιές»), όσο και σε μια σύμφωνη υπέρθεση (coherent superposition) των δύο καταστάσεων. Δηλαδή, το άτομο, έχει τη δυνατότητα να βρίσκεται τόσο στην κατάσταση 0, όσο και στην κατάσταση 1, ταυτόχρονα! Αν και η υπέρθεση είναι ένα φαινόμενο γνωστό στην κλασική φυσική, για παράδειγμα στην κυματική, εντούτοις η υπέρθεση κβαντικών καταστάσεων είναι εντελώς διαφορετικής φύσης, για την οποία δεν υπάρχει ανάλογο στον κλασικό κόσμο, (Dirac 1958). Αυτός είναι ο λόγος για τον οποίο είμαστε αναγκασμένοι να μιλάμε για κβαντικά bit ή qubit. Φυσικά, εφόσον στην καθημερινή μας ζωή έχουμε εμπειρίες μόνο κλασικών φαινομένων τέτοια φαινόμενα μάς φαίνονται πολύ παράξενα και δυσνόητα. Οι αναγνώστες αξίζει να έχουν υπόψη τους πως η υπέρθεση των δύο καταστάσεων καταρρέει όταν επιχειρήσουμε μια μέτρηση στο σύστημα [1]. Το αποτέλεσμα της μέτρησης μπορεί να είναι είτε 1 ή 0.
Ας δούμε, όμως, τις θεαματικές συνέπειες που μπορεί να έχει η ιδέα της υπέρθεσης. Ας σκεφτούμε έναν καταγραφέα που δημιουργείται από τρία bit. Κάθε κλασικός καταγραφέας τέτοιου τύπου μπορεί να αποθηκεύσει, σε μια δεδομένη στιγμή, μόνο έναν από οκτώ δυαδικούς αριθμούς, δηλαδή ο καταγραφέας μπορεί να βρίσκεται σε μια από οκτώ δυνατές καταστάσεις όπως 000, 001, 010, … 111. Ο αντίστοιχος κβαντικός καταγραφέας, μπορεί να αποθηκεύσει σε μια στιγμή, και τους οκτώ αριθμούς σε μια κβαντική υπέρθεση όλων των δυνατών καταστάσεων. Αυτό είναι κάτι εκπληκτικό. Αν συνεχίσουμε να προσθέτουμε qubit στον καταγραφέα αυξάνουμε την χωρητικότητα του εκθετικά, δηλαδή τρία qubit μπορούν να αποθηκεύσουν 8 διαφορετικούς αριθμούς ταυτόχρονα, τέσσερα qubit μπορούν να αποθηκεύσουν 16 διαφορετικούς αριθμούς και, γενικά, L qubit μπορούν να αποθηκεύσουν 2L αριθμούς. Από την στιγμή που ο καταγραφέας βρίσκεται σε μια σύμφωνη υπέρθεση αυτών των καταστάσεων, έχουμε τη δυνατότητα να εκτελέσουμε πράξεις με όλους αυτούς τους αριθμούς, δημιουργώντας, επί της ουσίας, μια νέου τύπου παράλληλη επεξεργασία πάνω σε ένα μόνο τμήμα του κβαντικού hardware. Για να εκτελέσει κάτι τέτοιο ένας κλασικός υπολογιστής θα πρέπει είτε να επαναλάβει τον ίδιο υπολογισμό 2L φορές ή να χρησιμοποιήσει 2L επεξεργαστές που θα εργάζονται παράλληλα. Με άλλα λόγια ο κβαντικός υπολογιστής, μας προσφέρει τεράστιο όφελος σε χρόνο και μνήμη.
Μια συνέπεια της αρχής της υπέρθεσης είναι η εμφάνιση του φαινομένου του κβαντικού εναγκαλισμού [2](quantum entanglement) ανάμεσα στις καταστάσεις δύο ή περισσότερων κβαντικών συστημάτων τα οποία έχουν αλληλεπιδράσει με κάποιο τρόπο ή έχουν δημιουργηθεί από κοινού μέσα από μια φυσική διαδικασία (Barnett 2009). Σε αυτήν την περίπτωση η κβαντική κατάσταση ενός από τα επιμέρους συστήματα δεν μπορεί να περιγραφεί ανεξάρτητα από την κατάσταση των άλλων ακόμη και στην περίπτωση που βρίσκονται σε πολύ μεγάλη απόσταση μεταξύ τους. Η κατάσταση των επιμέρους συστημάτων μπορεί να περιγραφεί μόνον ως κατάσταση ενός ενιαίου συστήματος (Penrose 2004). Ως έννοια, ο κβαντικός εναγκαλισμός, εισήχθη στη κβαντομηχανική για πρώτη φορά από τον Schrödinger το 1935, ο οποίος μάλιστα τον χαρακτήρισε και ως την ουσία της κβαντομηχανικής (Schrödinger 1935).
Τα κυκλώματα ενός υπολογιστή αποτελούνται από πολυάριθμες λογικές πύλες που συνδέονται, μέσω αγωγών, μεταξύ τους. Μια κβαντική λογική πύλη, όπως και μια κλασική, είναι μια απλή υπολογιστική διάταξη η οποία εκτελεί κάθε φορά μια στοιχειώδη κβαντική λειτουργία, συνήθως πάνω σε δύο qubit. Βέβαια, οι κβαντικές πύλες διαφέρουν από τις κλασικές, στο γεγονός ότι μπορούν να εκτελέσουν λειτουργίες πάνω σε σύμφωνες κβαντικές υπερθέσεις. Εντούτοις, καθώς ο αριθμός των κβαντικών πυλών σε ένα δίκτυο αυξάνεται, τότε, θα βρεθούμε αντιμέτωποι με κάποια σοβαρά πρακτικά προβλήματα. Η κατασκευή ενός κβαντικού υπολογιστή απαιτεί την εμπλοκή και συνεργασία ενός μεγάλου πλήθους από qubit και αυτό καθιστά εξαιρετικά δύσκολη τη διατήρηση του κβαντικού εναγκαλισμού μεταξύ των εμπλεκόμενων καταστάσεων ο οποίος αποτελεί «εκ των ων ουκ άνευ» συνθήκη για την λειτουργία ενός κβαντικού υπολογιστή. Είναι προφανές, λοιπόν, πως η διατήρηση του κβαντικού εναγκαλισμού αποτελεί το «σκληρό πυρήνα» του κβαντικού υπολογισμού.
ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΦΥΣΙΚΟΣ ΚΟΣΜΟΣ
Συνήθως θεωρούμε την υπολογιστική διαδικασία ως μια σειρά από μαθηματικές πράξεις και παραβλέπουμε πως επί της ουσίας η εκτέλεση ενός υπολογισμού είναι μια φυσική διαδικασία. Όπως χαρακτηριστικά συνόψισε ο R. Landauer, η επεξεργασία της πληροφορίας είναι ενδογενώς συνδεδεμένη με μια φυσική διαδικασία παρά με μια αφηρημένη έννοια και κατά συνέπεια ακολουθεί και αυτή τους νόμους της φύσης (Landauer 1991). Οι ηλεκτρονικοί υπολογιστές είναι, σε τελική ανάλυση, υλικά αντικείμενα και ως τέτοια δεν μπορούν παρά να υπακούουν στους νόμους της φύσης. Για παράδειγμα, η ταχύτητα μετάδοσης της πληροφορίας δεν μπορεί ποτέ να υπερβεί αυτήν του φωτός ενώ, καθώς οι διαστάσεις των διατάξεων μικραίνουν σε μέγεθος, ερχόμαστε πρόσωπο με πρόσωπο με τις «ιδιορρυθμίες» της κβαντομηχανικής.
ΚΒΑΝΤΙΚΗ ΥΠΕΡΘΕΣΗ ΚΑΙ ΚΒΑΝΤΙΚΟΣ ΕΝΑΓΚΑΛΙΣΜΟΣ
Η κατανόηση των εννοιών της υπέρθεσης και του κβαντικού εναγκαλισμού είναι αρκετά δύσκολη ακόμη και από επαγγελματίες φυσικούς και επιστήμονες καθώς, όπως αναφέραμε, τα κβαντικά φαινόμενα έρχονται σε αντίθεση με τη διαίσθησή μας. Ένα πολύ επιτυχημένο ανάλογο αυτών των δύο εννοιών οφείλουμε στον C. R. Monroe και στον κάτοχο του βραβείου Νόμπελ D. J. Wineland (Monroe 2008). Στο παράδειγμά τους χρησιμοποιούν ένα φαινόμενο που όλοι μας το έχουμε παρατηρήσει όταν προσπαθούμε να σχεδιάσουμε έναν κύβο πάνω σε ένα χαρτί όπου το μάτι μας συνήθως “ξεγελιέται” και δεν μπορεί να διακρίνει ποια πλευρά είναι μπροστά και πια πίσω. Αυτό είναι το ανάλογο της υπέρθεσης δύο κβαντικών καταστάσεων (Εικ. 1). Ο κύβος μας «αιωρείται» ανάμεσα σε δύο διαφορετικές καταστάσεις. Ακόμη πιο ενδιαφέρον είναι το γεγονός πως αν επιμείνουμε λίγο και εστιάσουμε σε μια από τις δύο πλευρές τότε αυτή «έρχεται» στο προσκήνιο αφήνοντας την άλλη στο «παρασκήνιο» και η «αιώρηση» παύει. Η καταστροφή αυτού του μετεικάσματος είναι το ανάλογο μιας μέτρησης σε ένα κβαντικό σύστημα.
Η περίπτωση του κβαντικού εναγκαλισμού είναι ανάλογη με τον σχεδιασμό δύο όμοιων κύβων (Εικ. 2). Σε αυτήν την περίπτωση το μάτι μας βλέπει και τους δύο κύβους πότε με την ίδια πλευρά μπροστά πότε με την άλλη. Κάθε προσπάθεια να εστιάσουμε το βλέμμα μας πάνω στον έναν από τους δύο κύβους («εκτέλεση μέτρησης») «αναγκάζει» τους κύβους να βρεθούν στην ίδια κατάσταση ανεξάρτητα αν μεταξύ τους δεν υπάρχει κάποια φυσική σύνδεση.
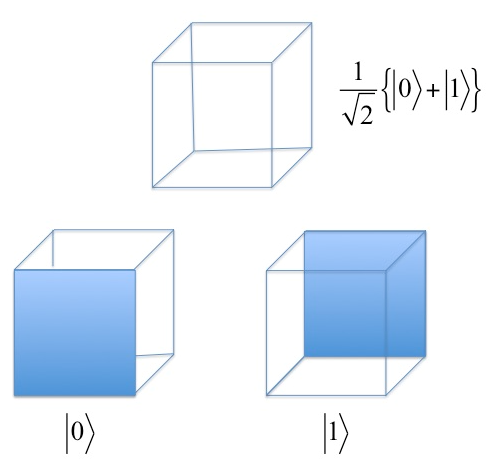
Εικ. 1: Κάθε φορά που σχεδιάζουμε έναν κύβο στο χαρτί, δημιουργείται ένα μετείκασμα με αποτέλεσμα για κάποιο χρονικό διάστημα να μην είμαστε σε θέση να διακρίνουμε ποια πλευρά βρίσκεται μπροστά και πια πίσω. Ο κύβος σε αυτήν την περίπτωση (επάνω) βρίσκεται σε μια «υπέρθεση» δύο διαφορετικών καταστάσεων. Αν επιμείνουμε συγκεντρώνοντας το βλέμμα μας σε μια από τις δύο πλευρές τότε βλέπουμε ως μπροστινή είτε την μια (|0>) ή την άλλη (|1>). Αυτό ισοδυναμεί με το να έχουμε κάνει μια μέτρηση.
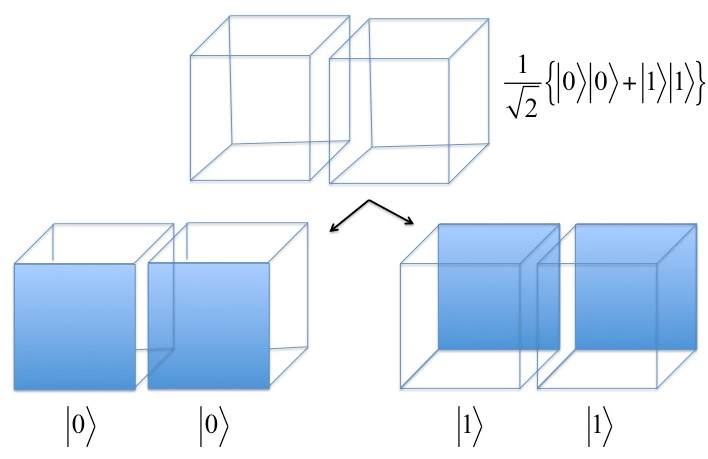
Εικ. 2: Στην περίπτωση αυτή βλέπουμε μια εναγκαλισμένη κατάσταση (επάνω). Το μάτι μας βλέπει τους δύο κύβους πότε με την ίδια πλευρά μπροστά (|0>|0>) πότε με την άλλη ((|1>|1>). Κάθε προσπάθεια (κάτω) να συγκεντρωθούμε πάνω στο σχήμα (μέτρηση) αναγκάζει τους κύβους να βρεθούν στην ίδια κατάσταση ανεξάρτητα αν μεταξύ τους δεν υπάρχει μια φυσική σύνδεση.
Όπως έχει γραφεί, ο κβαντικός εναγκαλισμός μπορεί να θεωρηθεί σαν ένας «αόρατος αγωγός» ανάμεσα στα σωματίδια για τον οποίο δεν υπάρχει αντίστοιχο κλασικό ανάλογο (Monroe 2008). Μια εναγκαλισμένη κατάσταση μπορεί να περιέχει περισσότερη πληροφορία από αυτήν που πιθανόν να περιέχεται σε οποιαδήποτε κλασική κατάσταση με τον ίδιο αριθμό σωματιδίων. Το πρόβλημα που υπάρχει με αυτές τις καταστάσεις είναι η ταχύτατη απώλεια των κβαντικών συσχετίσεων λόγω των επιδράσεων του περιβάλλοντος. Πολλοί πιστεύουν πως αυτό και μόνο το γεγονός θέτει όρια στον κβαντικό υπολογισμό. Για αυτόν τον λόγο τα qubit πρέπει να είναι επαρκώς απομονωμένα από το περιβάλλον καθώς οποιεσδήποτε εξωτερικές αλληλεπιδράσεις καταστρέφουν τον κβαντικό εναγκαλισμό και διακόπτουν τον κβαντικό υπολογισμό. Ταυτόχρονα τα qubit πρέπει να αλληλεπιδρούν ισχυρά μεταξύ τους ενώ στο τέλος θα πρέπει να εκτελούνται σε αυτά ακριβείς μετρήσεις ώστε να αποκαλύπτονται τα αποτελέσματα των υπολογισμών. Τα τελευταία χρόνια ο κβαντικός εναγκαλισμός έχει επιβεβαιωθεί σε μια σειρά πειραμάτων στα οποία τα εναγκαλισμένα σωματίδια απέχουν πολλά χιλιόμετρα μακριά (Yu 2020). Με ταχύτατους ρυθμούς ο κβαντικός εναγκαλισμός εξελίσσεται από ένα ζήτημα εργαστηριακής διερεύνησης των θεμελίων της κβαντομηχανικής σε μια πανίσχυρη τεχνολογία. Ήδη στο διάστημα περιφέρονται δορυφόροι που χρησιμοποιούν τον κβαντικό εναγκαλισμό για την κωδικοποίηση και απόκρυψη των μηνυμάτων που μεταδίδουν (Yin 2017).
Κλείνοντας το άρθρο αξίζει να αναφέρουμε ακόμη μια σημαντική συνεισφορά του Feynman. Σε μια από τις διαλέξεις του στο Caltech, ο Feynman συσχέτισε την ανάγκη ύπαρξης των κβαντικών υπολογιστών με τη δυσκολία που αντιμετωπίζει ένας κλασικός υπολογιστής να προσομοιώσει ακόμη και τις πιο απλές κβαντικές διαδικασίες. Όπως έχει αποδείξει πολλές φορές η ιστορία, εκεί που τα πράγματα δείχνουν να φθάνουν σε ανυπέρβλητα εμπόδια, είναι η ώρα των μεγάλων επιστημόνων. Ο Feynman αντιλήφθηκε σωστά ότι το πρόβλημα ήταν με το κεφάλι στη γη και τα πόδια στον ουρανό. Απλά αποφάσισε να το αντιστρέψει και να μετατρέψει τη δυσκολία σε ευκαιρία. Η σκέψη του ήταν απλή: εφόσον χρειαζόμαστε ένα τεράστιο υπολογιστικό έργο για να προσομοιώσουμε ένα πείραμα, τότε μπορούμε να θεωρήσουμε το ίδιο το πείραμα, από το στήσιμο μέχρι την τελική μέτρηση, ως ισοδύναμο μιας πολύπλοκης διαδοχής υπολογισμών και τελικά ως υπολογισμό καθαυτό. Με αυτήν τη λογική ο Feynman πρότεινε ότι θα ήταν δυνατόν να προσομοιώσουμε μια κβαντική διαδικασία με δεδομένο ότι ο προσομοιωτής θα είναι ο ίδιος ένα απλούστερο κβαντικό σύστημα. Η κβαντική προσομοίωση είναι ένα από τα πιο συναρπαστικά και ταχύτερα αναπτυσσόμενα πεδία της φυσικής του 21ου αιώνα και έχει άρρηκτη σχέση με την αναγέννηση της ατομικής φυσικής (Lembessis 2020)
ΕΡΓΑ ΤΟΥ FEYNMAN
“The Feynman lectures in physics”, “Statistical mechanics”, “Photon-hadron Interactions”, “Theory of Fundamental Processes”, “Quantum Mechanics and Path Integrals”, “Lectures on Gravitation”, “Feynman’s Tips On Physics: A Problem-Solving Supplement to the Feynman Lectures On Physics”, “Elementary Particles and the Laws of Physics: The 1986 Dirac Memorial Lectures”, «QED: Κβαντική Ηλεκτροδυναμική», «Σίγουρα θ’ αστειεύεστε κύριε Φάινμαν », «Τι σε νοιάζει εσένα τι σκέφτονται οι άλλοι», «Η χαμένη διάλεξη του Feynman», «Έξι εύκολα κομμάτια», «Έξι όχι τόσο εύκολα κομμάτια», «Η χαρά της ανακάλυψης».
ΒΙΒΛΙΟΓΡΑΦΙΑ
Barnett S. M., 2009. Quantum Information. Oxford UK: Oxford University Press, p. 115.
Deutsch D., 1985. Quantum theory: the Church–Turing principle and the universal quantum computer. Proceedings of the Royal Society of London A 400 (1818), p.97.
Dirac P. A. M. 1958. The Principles of Quantum Mechanics, 4th edition. Oxford UK: Oxford University Press, p. 14.
Feynman R. P., 1982. Simulating physics with computers. Int. J. Theor. Phys., 21, p. 467.
Feynman R. P., 2005. Η χαρά της ανακάλυψης. Αθήνα: ΚΑΤΟΠΤΡΟ.
Feynman R. P., 2006. Διαλέξεις για τους υπολογιστές. Αθήνα: Leader Books.
Feynman R. P., 2018. Σίγουρα θα αστειεύεστε, κύριε Φάινμαν! Αθήνα: ΚΑΤΟΠΤΡΟ.
Landauer R. , 1991. Information is physical. Physics Today 44(5), p. 23.
Lembessis V. E., 2020. Taming Atoms: The Renaissance of Atomic Physics. Bellingham, Washington USA: SPIE.
Monroe C. R. and Wineland D. J., 2008. Quantum computing with ions. Scientific American, Issue 8, p. 64.
Penrose R., 2004. The Road to Reality: A complete guide to the laws of universe, New York, Alfred A. Knopf, p.578.
Rivest R. I., Shamir A. , and Adelman L. M., 1979. On digital signatures and public key cryptosystems. MIT Laboratory for Computer Science, Technical Report, MIR/LCS/TR-212.
Shor P., 1994. Algorithms for quantum computation: Discrete logarithms and factoring. Proceedings of the 35th Annual Symposium on the Foundations of Computer Science. New York: IEEE Computer Society Press.
Schrödinger Ε., 1935. Probability relations between separated systems. Proc. Camb. Phil. Soc., 31, p.555.
Yu Y., Ma F. et al, 2020. Entanglement of two quantum memories via fibres over dozens of kilometres. Nature, 578, p.240.
Yin J., Cao Y. et al, 2017. Satellite-based entanglement distribution over 1200 kilometers. Science, 356, p.1140.





